1 256 As A Percentage
catronauts
Sep 16, 2025 · 5 min read
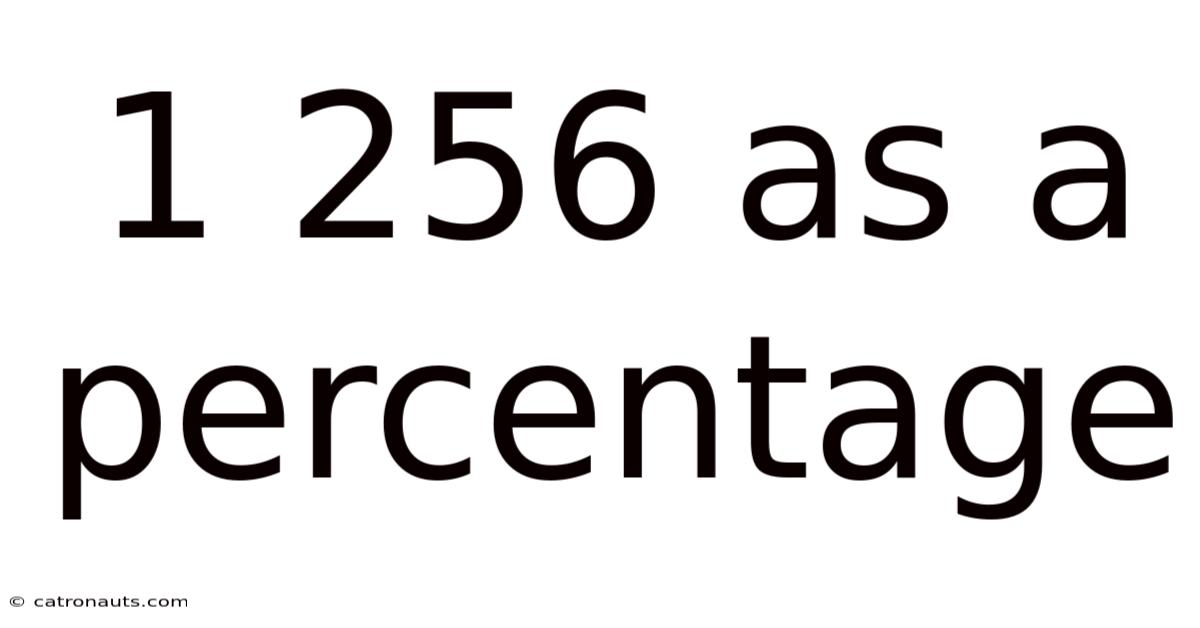
Table of Contents
1/256 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday life. This article delves deep into converting the fraction 1/256 into a percentage, explaining the process step-by-step and exploring related concepts. We'll cover the calculation, its applications, and answer frequently asked questions to provide a comprehensive understanding. This detailed guide will equip you with the knowledge to confidently tackle similar fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the specific calculation of 1/256 as a percentage, let's briefly review the core concepts. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts, while the numerator indicates how many of those parts are being considered.
A percentage, denoted by the symbol %, represents a fraction where the denominator is always 100. It indicates the proportion of a value relative to 100. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 1/256 to a Percentage: The Step-by-Step Process
To convert 1/256 to a percentage, we need to transform the fraction into an equivalent fraction with a denominator of 100. However, directly converting 256 to 100 isn't straightforward. Instead, we'll follow a more general approach:
Step 1: Convert the Fraction to a Decimal
The first step involves converting the fraction 1/256 into a decimal. We achieve this by dividing the numerator (1) by the denominator (256):
1 ÷ 256 = 0.00390625
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.00390625 × 100 = 0.390625
Therefore, 1/256 is equal to 0.390625%.
Step 3: Rounding (Optional)
Depending on the level of precision required, you might need to round the percentage. For instance, rounding to two decimal places gives us 0.39%. Rounding to one decimal place would give 0.4%. The appropriate level of rounding depends on the context of the problem.
Alternative Method: Using Proportions
Another way to approach this conversion involves setting up a proportion:
1/256 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
256x = 100
x = 100/256
x = 0.390625
Multiplying by 100 to express this as a percentage gives us 0.390625%, the same result as the previous method.
Applications of this Conversion
Understanding how to convert fractions like 1/256 to percentages has practical applications in numerous scenarios:
- Finance: Calculating interest rates, discounts, or profit margins often involves working with fractions and percentages. For example, if a stock price drops by 1/256 of its initial value, understanding its percentage decrease is crucial for investment analysis.
- Statistics: Representing data proportions as percentages is essential for data visualization and interpretation. Imagine analyzing survey results where 1 out of 256 respondents chose a particular option; converting this fraction to a percentage provides a more readily understandable representation.
- Science: Expressing experimental error or uncertainty often involves percentages. For example, if a measurement has a margin of error of 1/256, converting this fraction to a percentage provides a clear picture of the accuracy.
- Everyday Life: Percentage calculations are used frequently in everyday life, from calculating tips and sales tax to understanding discounts and proportions in recipes.
Scientific Notation and Significant Figures
For very small percentages like 0.390625%, scientific notation can be a more concise way to represent the value. This would be expressed as 3.90625 x 10⁻². Additionally, the concept of significant figures becomes relevant when dealing with precision. Since the original fraction 1/256 is exact, the number of significant figures depends on the level of rounding applied to the final percentage.
Further Exploration: Understanding Smaller Fractions
Understanding how 1/256 translates to a percentage provides a foundation for tackling similar calculations with even smaller fractions. The process remains the same: divide the numerator by the denominator to obtain a decimal, then multiply by 100 to convert to a percentage. The smaller the fraction, the smaller the resulting percentage will be. This emphasizes the relationship between the size of the fraction and its percentage equivalent.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to convert 1/256 to a percentage?
A1: Yes, absolutely! Most calculators have the functionality to perform this conversion directly. Simply divide 1 by 256 and then multiply the result by 100.
Q2: Why is the percentage so small?
A2: The percentage is small because the fraction 1/256 represents a very small part of the whole. The denominator (256) is significantly larger than the numerator (1), indicating that only a tiny portion is being considered.
Q3: Are there other ways to express 1/256 besides as a percentage?
A3: Yes, you can express 1/256 as a decimal (0.00390625) or in scientific notation (3.90625 x 10⁻³).
Q4: What if the numerator wasn't 1? For example, what about 5/256?
A4: The process remains the same. You would divide 5 by 256 to get the decimal, and then multiply by 100 to get the percentage. 5/256 = 0.01953125 which is 1.953125%.
Conclusion:
Converting 1/256 to a percentage illustrates the fundamental connection between fractions and percentages. The conversion process, whether using division and multiplication or proportions, is straightforward and applicable to a wide range of fractions. Understanding this conversion is essential for various applications across numerous fields, and the ability to perform this calculation accurately and confidently empowers you to tackle more complex mathematical problems in the future. This detailed explanation, along with the provided examples and frequently asked questions, aims to provide a thorough understanding of this important mathematical concept. Remember to always consider the context and choose an appropriate level of rounding for your final answer.
Latest Posts
Latest Posts
-
Tel Aviv Map Of Israel
Sep 17, 2025
-
Awareness Interest Evaluation Trial Adoption
Sep 17, 2025
-
V For Vendetta Speech V
Sep 17, 2025
-
What Element Has 18 Neutrons
Sep 17, 2025
-
What Rhymes With In Love
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 256 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.