1 3 Of A Turn
catronauts
Sep 14, 2025 · 6 min read
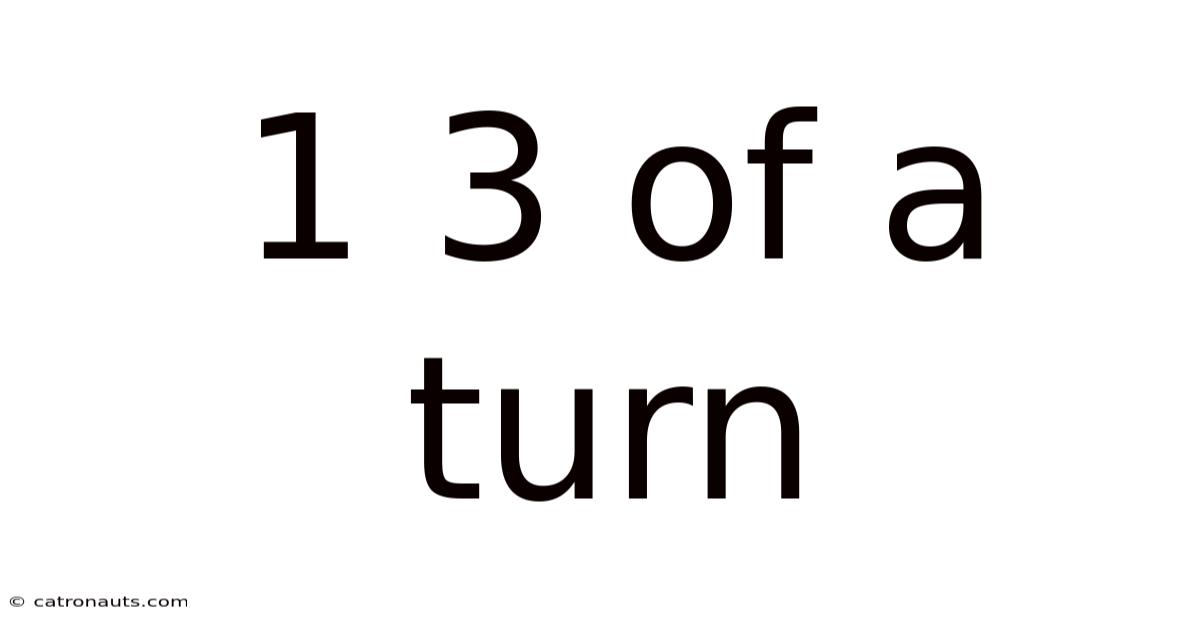
Table of Contents
Understanding 1 1/3 Turns: A Comprehensive Guide
Have you ever encountered the term "1 1/3 turns" in a technical manual, a DIY project, or even a puzzle? This seemingly simple phrase can represent a surprisingly complex concept, especially when dealing with rotational mechanics, specific applications, and nuanced interpretations. This article delves deep into the meaning, applications, and implications of a 1 1/3 turn, providing a comprehensive understanding suitable for various levels of expertise. We'll explore its use in different contexts, address common misconceptions, and offer practical examples to solidify your understanding.
What Exactly is a 1 1/3 Turn?
At its core, a 1 1/3 turn refers to a rotation of an object around its axis by an angle equivalent to one full rotation plus one-third of a full rotation. A full rotation is defined as 360 degrees or 2π radians. Therefore, 1 1/3 turns equates to:
- Degrees: 1 x 360° + (1/3) x 360° = 360° + 120° = 480°
- Radians: 1 x 2π + (1/3) x 2π = 2π + (2π/3) = (8π/3) radians
This seemingly straightforward calculation has significant implications across various fields. Understanding this fundamental concept allows us to accurately predict and control the movement and positioning of rotating objects.
Applications of 1 1/3 Turns: Across Diverse Fields
The concept of a 1 1/3 turn finds applications in many surprising areas. Let's explore a few key examples:
1. Engineering and Mechanics:
-
Gear Ratios: In mechanical systems involving gears, a 1 1/3 turn ratio could describe the relationship between the input and output shafts. For instance, if the input gear makes one and a third turn, the output gear might complete one full rotation. This is crucial in designing systems that require specific speed or torque adjustments. Understanding this ratio is essential for calculating gear teeth counts and designing efficient gear trains.
-
Rotary Actuators: Many industrial processes utilize rotary actuators—devices that convert rotational motion into linear or other types of movement. Precise control over the angle of rotation is crucial. A specific application might require a 1 1/3 turn of an actuator to achieve the desired position or result.
-
Robotics: In robotics, the precise movement of robotic arms and joints often involves fractional turns. Programming a robot arm to rotate 1 1/3 turns ensures accurate positioning for tasks like welding, painting, or material handling. Incorrect angles can lead to significant errors and malfunctions.
2. Construction and Manufacturing:
-
Screw Fasteners: Although less frequently encountered than whole or half turns, the concept can apply to screw mechanisms. Certain specialized screws or fastening systems might require a 1 1/3 turn for complete engagement or locking. Understanding this is crucial for proper installation and preventing malfunctions.
-
Lathe Operations: In machining using a lathe, precise rotations are critical for creating specific shapes and dimensions. A 1 1/3 turn of the workpiece might be needed to achieve a desired cut or surface finish.
-
3D Printing: Some 3D printing processes involve rotational elements. Calibrating the rotational mechanism might involve setting precise angles, possibly including fractional turns.
3. Puzzles and Games:
-
Combination Locks: While less common than simpler fractional turns, some complex combination locks could utilize a sequence involving a 1 1/3 turn at a particular stage. This adds an extra layer of security.
-
Mechanical Puzzles: Many intricate mechanical puzzles rely on precise movements and rotations. A 1 1/3 turn might be necessary to unlock a particular mechanism or solve a specific part of the puzzle.
Understanding the Nuances: Dealing with Fractional Turns
While conceptually straightforward, working with fractional turns requires careful consideration of several factors:
-
Units: Consistency is paramount. Ensure you are working consistently with either degrees or radians to avoid errors.
-
Accuracy: In many applications, precise angular measurements are crucial. Using appropriate measuring tools and techniques is vital for achieving the desired result. Slight deviations from the intended 1 1/3 turns can have significant consequences.
-
Interpolation: In situations where only discrete steps are possible (e.g., digital control systems), it might be necessary to interpolate between available steps to approximate a 1 1/3 turn. This requires careful consideration of the resolution of the system.
-
Over-Rotation and Under-Rotation: Both overshooting and undershooting the target angle of 480° can lead to errors. Careful calibration and control mechanisms are crucial to prevent these issues.
Practical Examples and Calculations
Let's illustrate the practical application of 1 1/3 turns with a few examples:
Example 1: Gear Ratio
Suppose two gears are meshed, and the driver gear has 60 teeth, while the driven gear has 45 teeth. If the driver gear rotates 1 1/3 turns, how many turns will the driven gear make?
- Driver gear turns: 1 1/3 = 4/3 turns
- Gear ratio: 60 teeth / 45 teeth = 4/3
- Driven gear turns: (4/3) turns * (4/3) = 16/9 turns ≈ 1.78 turns
Example 2: Rotary Actuator
A rotary actuator has a resolution of 0.1 degrees. How many steps are needed to achieve a rotation of 1 1/3 turns?
- 1 1/3 turns = 480 degrees
- Steps per degree: 1 / 0.1 = 10 steps/degree
- Total steps: 480 degrees * 10 steps/degree = 4800 steps
Frequently Asked Questions (FAQs)
Q: Can a 1 1/3 turn be represented as a decimal?
A: Yes, a 1 1/3 turn can be represented as 1.333... turns (a repeating decimal). However, in many engineering contexts, using the fraction 4/3 is often preferred for accuracy and to avoid potential rounding errors.
Q: What happens if I rotate something more or less than 1 1/3 turns?
A: The outcome depends on the specific application. In some cases, slight deviations might be acceptable, while in others, even small errors can have significant consequences, leading to malfunction or inaccuracy.
Q: How can I measure a 1 1/3 turn accurately?
A: The best method depends on the application. For smaller objects, a protractor or digital angle gauge might be sufficient. For larger systems, more sophisticated measuring techniques, possibly involving encoders or other sensors, could be necessary.
Q: Are there any safety concerns associated with working with rotational mechanisms requiring fractional turns?
A: Yes, always exercise caution when dealing with rotating machinery. Proper safety procedures, including lockout/tagout procedures, should always be followed to prevent accidents.
Conclusion: Mastering the Art of Fractional Rotations
Understanding the concept of a 1 1/3 turn, while seemingly simple, is crucial for success in many fields. From engineering and manufacturing to puzzles and robotics, mastering this concept enables more precise control and predictable outcomes. By understanding the calculations, practical applications, and potential nuances, you can confidently navigate scenarios that involve these fractional rotations. Remember that accuracy, precision, and appropriate safety measures are paramount when working with any rotating systems.
Latest Posts
Latest Posts
-
Peop Model Occupational Therapy Example
Sep 14, 2025
-
Alexandre Cabanel Birth Of Venus
Sep 14, 2025
-
William Wordsworth Poem On Daffodils
Sep 14, 2025
-
How Much Is 1 8 L
Sep 14, 2025
-
Hotel Near Kl Twin Tower
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Of A Turn . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.