1 50 As A Percent
catronauts
Sep 15, 2025 · 5 min read
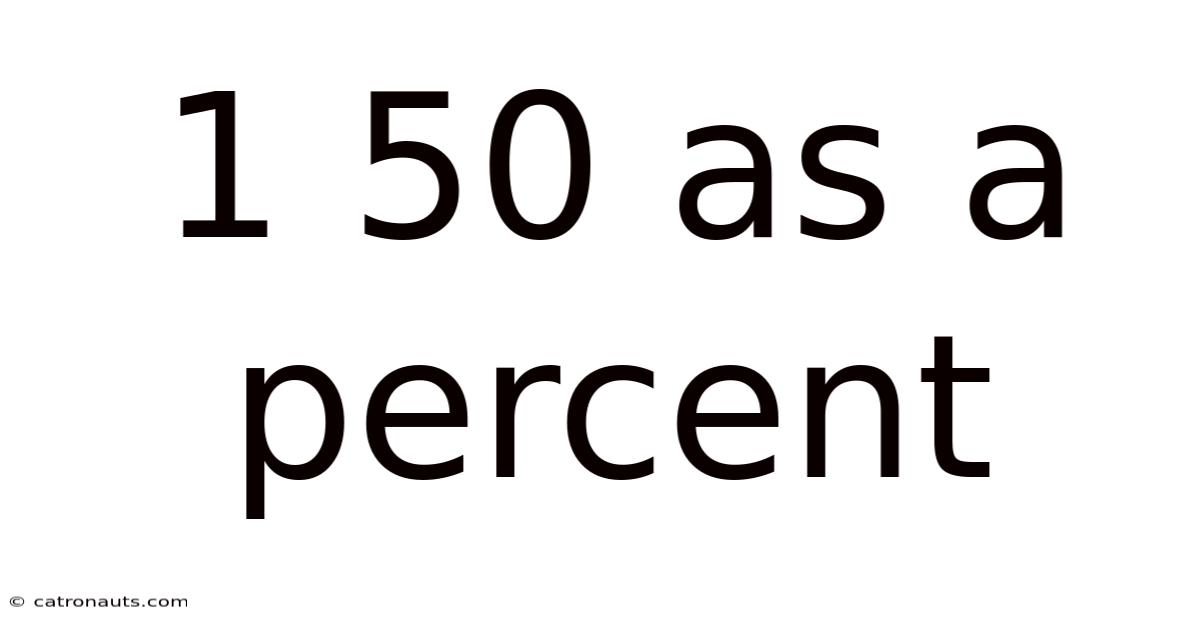
Table of Contents
1/50 as a Percent: Understanding Fractions, Decimals, and Percentages
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday calculations. This comprehensive guide will delve into the process of converting the fraction 1/50 into a percentage, explaining the underlying principles and offering practical examples to solidify your understanding. We'll explore the relationship between fractions, decimals, and percentages, providing you with a robust foundation for tackling similar conversions in the future.
Introduction: Fractions, Decimals, and Percentages – A Triad of Representation
Before we dive into converting 1/50 to a percentage, let's briefly review the interconnectedness of fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 1/50 means one part out of fifty equal parts.
-
Decimals: Represent a part of a whole using a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on.
-
Percentages: Represent a part of a whole as a fraction of 100. The symbol "%" signifies "per hundred."
These three forms are interchangeable, and understanding their relationships is crucial for mathematical fluency. Converting between them involves straightforward calculations, as we'll see with the example of 1/50.
Converting 1/50 to a Decimal
The first step in converting 1/50 to a percentage is transforming it into a decimal. To do this, we simply divide the numerator (1) by the denominator (50):
1 ÷ 50 = 0.02
Therefore, 1/50 is equal to 0.02 as a decimal.
Converting the Decimal to a Percentage
Now that we have the decimal equivalent (0.02), converting it to a percentage is a simple multiplication. To express a decimal as a percentage, we multiply it by 100 and add the "%" symbol:
0.02 × 100 = 2%
Therefore, 1/50 is equivalent to 2%.
Understanding the Process: A Deeper Dive
Let's break down the conversion process in more detail, focusing on the underlying mathematical principles.
The core idea behind converting a fraction to a percentage is to express the fraction as an equivalent fraction with a denominator of 100. While we could have directly converted 1/50 to a percentage by finding an equivalent fraction with a denominator of 100, the decimal conversion method is generally more efficient, especially for fractions that don't easily convert to a denominator of 100.
To illustrate the equivalent fraction method:
We need to find a number that, when multiplied by 50, gives us 100. That number is 2 (50 x 2 = 100). To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by the same number:
(1 × 2) / (50 × 2) = 2/100
Since a percentage is a fraction out of 100, 2/100 directly translates to 2%.
Practical Applications of 1/50 as a Percentage
The conversion of 1/50 to 2% has many practical applications across various disciplines. Here are a few examples:
-
Finance: Calculating interest rates, discounts, or profit margins. Imagine a 2% discount on a purchase; this represents a saving of 1/50 of the original price.
-
Statistics: Representing data proportions or probabilities. If 2 out of every 100 people in a survey responded in a particular way, this could be expressed as 2%, which is equivalent to 1/50.
-
Science: Expressing experimental results or measurements. A 2% error in a scientific experiment might be represented as 1/50 of the expected value.
-
Everyday Life: Calculating tips, sharing amounts, or understanding sales promotions.
Different Methods for Percentage Calculation
While we’ve primarily focused on converting 1/50 to a percentage via the decimal method, there are other approaches depending on the complexity of the fraction:
-
Direct Conversion (for simpler fractions): If the denominator is a factor of 100 (like 1/25 or 1/10), you can directly scale up the fraction to get an equivalent fraction with a denominator of 100. For example, 1/25 becomes 4/100 which is 4%.
-
Using a Calculator: A calculator can efficiently handle division and multiplication, making the conversion from fraction to decimal to percentage quicker.
-
Cross-Multiplication: For more complex fractions, cross-multiplication can be utilized, particularly when comparing percentages.
-
Proportions: Setting up a proportion can help solve problems involving fractions and percentages.
Advanced Concepts and Applications
The fundamental understanding of converting fractions to percentages can be extended to more complex scenarios:
-
Calculating Percentage Change: This involves finding the percentage increase or decrease between two values.
-
Compound Interest: This concept builds upon percentage calculations, incorporating the effect of interest earned on both the principal and accumulated interest.
-
Statistical Analysis: Percentages are integral to interpreting data and drawing inferences.
Frequently Asked Questions (FAQ)
-
Q: Can all fractions be converted to percentages?
- A: Yes, all fractions can be converted to percentages. The process involves dividing the numerator by the denominator to get a decimal and then multiplying by 100 to obtain the percentage.
-
Q: What if the resulting decimal has many digits after the decimal point?
- A: You can round the decimal to a desired level of accuracy (e.g., to two decimal places). However, for exact calculations, it’s advisable to retain as many decimal places as needed.
-
Q: Are there any limitations to using percentages?
- A: While percentages are useful for representing parts of a whole, they can be misleading if the total amount is not clearly defined or if percentages are compared across different total amounts.
Conclusion: Mastering the Conversion of Fractions to Percentages
Converting 1/50 to a percentage, resulting in 2%, is a straightforward process involving converting the fraction to a decimal and then to a percentage. This seemingly simple conversion is a foundational element in various mathematical and real-world applications. Understanding the underlying principles and different methods for converting fractions to percentages will equip you with a valuable skill set for navigating numerous situations requiring numerical proficiency. The ability to easily translate between fractions, decimals, and percentages significantly enhances mathematical literacy and problem-solving capabilities. Remember to practice the conversion process with different fractions to solidify your understanding and build confidence in your mathematical skills. Through consistent practice and a deeper exploration of related concepts, you can develop a comprehensive grasp of percentage calculations and their significance in various fields.
Latest Posts
Latest Posts
-
Is A Diamond A Mixture
Sep 15, 2025
-
Tallest Waterfall In South America
Sep 15, 2025
-
Do Other Animals Get Pimples
Sep 15, 2025
-
Symbol Of The Holy Eucharist
Sep 15, 2025
-
Nonfiction Text With Text Features
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.