1 9 As A Percent
catronauts
Sep 18, 2025 · 6 min read
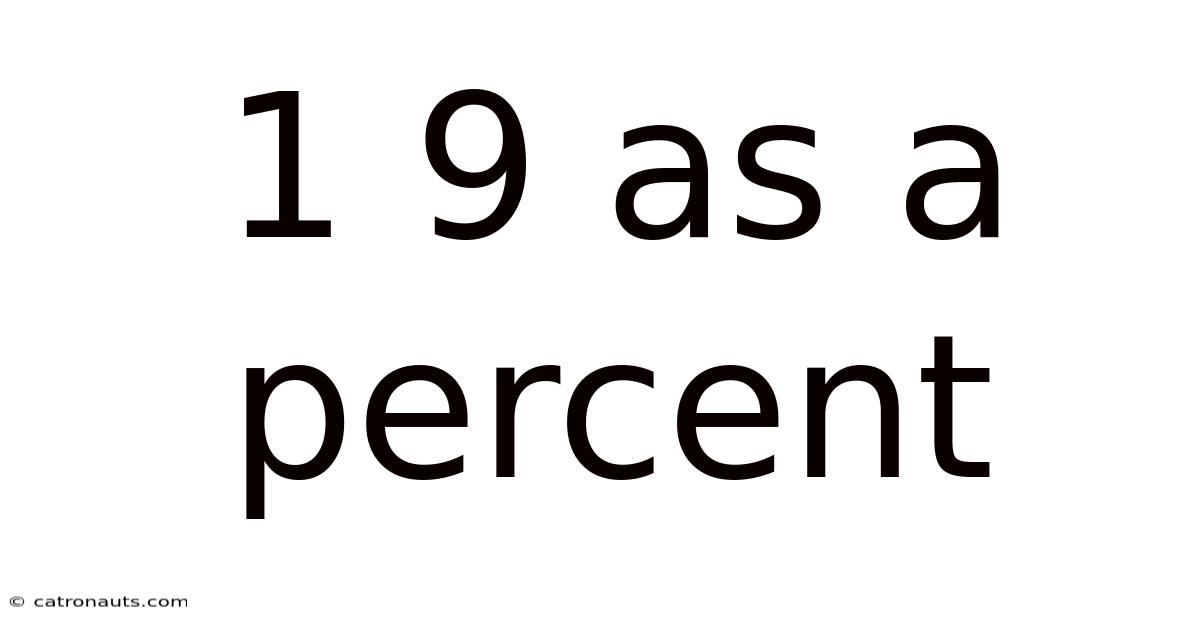
Table of Contents
Understanding 1/9 as a Percentage: A Comprehensive Guide
Many everyday situations require converting fractions to percentages. Understanding how to do this is crucial for budgeting, calculating discounts, interpreting statistical data, and much more. This article provides a comprehensive guide to converting the fraction 1/9 into a percentage, explaining the underlying mathematical principles and offering various methods to solve the problem. We'll delve into the calculation process, explore the significance of this specific conversion, and answer frequently asked questions. By the end, you'll not only know the answer but also understand how to tackle similar fraction-to-percentage conversions confidently.
Introduction: From Fractions to Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Fractions, on the other hand, represent a part of a whole. Converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100, then expressing the numerator as the percentage. This seemingly simple process underpins many mathematical applications. Let's explore how to transform the fraction 1/9 into its percentage equivalent.
Method 1: Direct Conversion using Division
The most straightforward method to convert 1/9 to a percentage is through division. A fraction essentially represents a division problem: the numerator (top number) divided by the denominator (bottom number).
-
Divide the numerator by the denominator: 1 ÷ 9 = 0.111111... This result is a decimal.
-
Multiply the decimal by 100: 0.111111... × 100 = 11.1111...%
Therefore, 1/9 is approximately 11.11%. The repeating decimal indicates that this percentage is an approximation. We can round it to a desired level of precision, such as 11.11% or even 11.1%. The more decimal places we use, the more accurate the representation.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves manipulating the fraction to create an equivalent fraction with a denominator of 100. While this approach might seem more complex initially, it reinforces the fundamental concept of equivalent fractions.
Unfortunately, there's no whole number we can multiply 9 by to get 100. This means we need to use division and rounding. Let's think about it this way:
We want to find a number x such that:
(1/9) * x = y/100
Solving for x:
x = (9y)/100
Since x must be a whole number for this method to directly work, and it is difficult to find a whole number to solve this problem perfectly. We'll have to approximate.
This method is less practical for 1/9, as it leads to an approximation similar to Method 1. However, this method becomes extremely useful for fractions where the denominator is a factor of 100 (such as 1/4, 1/2, 1/5, etc.). For example, to convert 1/4 to a percentage, we would multiply both numerator and denominator by 25 (100/4 = 25): (1 x 25) / (4 x 25) = 25/100 = 25%.
Method 3: Using a Calculator
Most calculators have a fraction-to-decimal conversion function. Simply input the fraction 1/9 and press the equals button. The calculator will display the decimal equivalent (0.1111...). Multiplying this decimal by 100 will give you the percentage (approximately 11.11%).
The Significance of 11.11% (approximately)
While the percentage approximation for 1/9 might seem insignificant on its own, its understanding extends beyond simple calculations. It's a fundamental building block for understanding more complex scenarios:
- Financial Calculations: Imagine calculating a discount of 1/9 off an item. This understanding would be vital.
- Statistical Analysis: If 1/9 of a sample population exhibits a specific characteristic, representing that as a percentage helps visualize the proportion.
- Probability and Odds: Understanding the probability of an event occurring with a 1/9 chance is essential in various applications.
- Geometric Progressions: The number 0.1111... is also related to geometric series, where understanding the fraction's decimal representation becomes invaluable.
Therefore, the seemingly simple conversion of 1/9 to a percentage connects to larger, more complex mathematical concepts.
Understanding Repeating Decimals
The result of 1 ÷ 9 (0.1111...) is a repeating decimal. This means the digit 1 repeats infinitely. We can represent this using a bar notation: 0.1̅. Understanding repeating decimals is crucial for accurate calculations and prevents rounding errors from accumulating in complex computations.
Practical Applications: Real-world Scenarios
Let's look at a few real-world examples where understanding 1/9 as a percentage is helpful:
- Sales Discounts: A store offers a 1/9 discount on all items. To find the discounted price, you would calculate 11.11% of the original price and subtract it from the original price.
- Survey Results: In a survey of 900 people, 100 responded positively to a question. This represents 100/900 = 1/9, or approximately 11.11% of the respondents.
- Resource Allocation: If you have 900 units of a resource and need to allocate 1/9 of them to a specific task, you need to allocate approximately 100 units.
Frequently Asked Questions (FAQ)
-
Q: Is 11.11% the exact equivalent of 1/9? A: No, it's an approximation due to the repeating decimal nature of 1/9. The precise representation is 11.111...%, where the 1s repeat infinitely.
-
Q: How can I avoid rounding errors when using 1/9 as a percentage? A: In most cases, rounding to two or three decimal places (11.11% or 11.111%) is sufficient. For highly precise calculations, keep the fraction form (1/9) as long as possible before converting to a percentage at the final stage.
-
Q: Why is it important to understand different methods for converting fractions to percentages? A: Using different methods provides a deeper understanding of the underlying mathematical principles. It also equips you with alternative approaches depending on the context of the problem and the tools available.
-
Q: Can I use a different fraction to illustrate this process? A: Absolutely! This process applies to any fraction. For example, you could try converting 2/9, 3/9, or even more complex fractions to practice. The key is to understand the division and multiplication principles involved.
-
Q: Are there any online tools to convert fractions to percentages? A: Yes, many websites and apps offer fraction-to-percentage converters. These tools can be useful for verifying calculations or solving more complex fraction conversions. (Note: We are not providing links to external websites in this article).
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill with broad applications. We've explored multiple methods for converting 1/9 to a percentage, highlighting the significance of understanding repeating decimals and the importance of accuracy. This detailed explanation not only provides the answer (approximately 11.11%) but also empowers you to tackle similar conversions with confidence, strengthening your overall mathematical understanding and problem-solving abilities. Remember, practice is key to mastering this skill, so try converting other fractions to percentages to further enhance your understanding.
Latest Posts
Latest Posts
-
Food Chain Of A Grassland
Sep 18, 2025
-
The Giver Summary All Chapters
Sep 18, 2025
-
When Was Sign Language Invented
Sep 18, 2025
-
The Big Sleep Movie Cast
Sep 18, 2025
-
Hansel And Gretel 2002 Movie
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 9 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.