1 X 2 Y 2
catronauts
Sep 16, 2025 · 6 min read
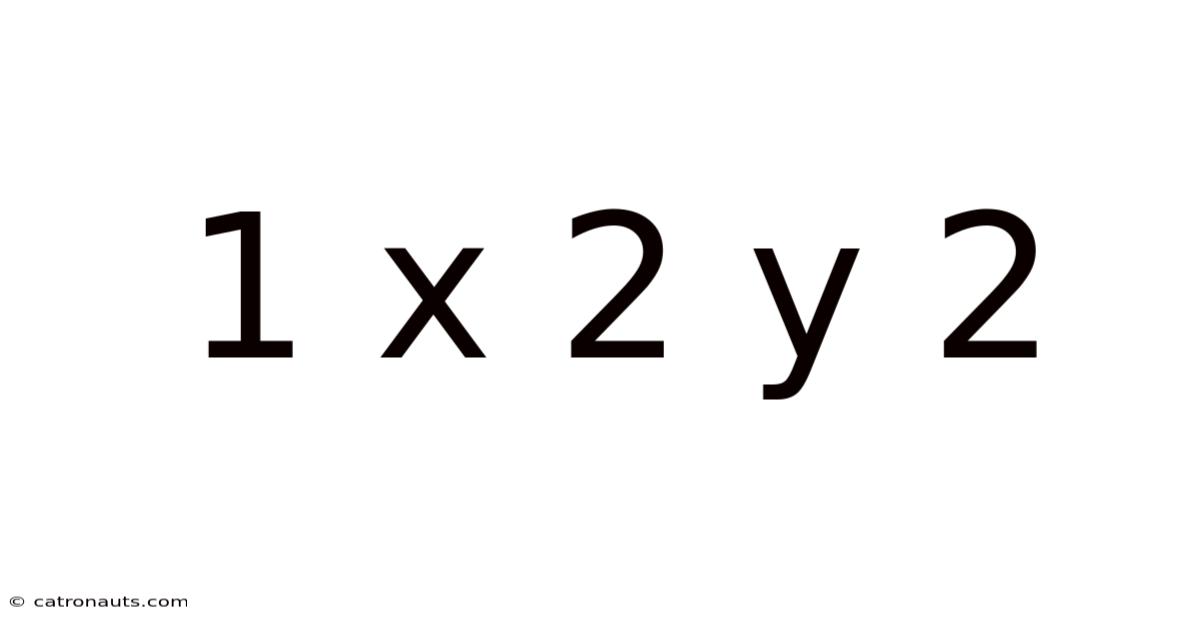
Table of Contents
Decoding the Mathematical Mystery: A Deep Dive into 1 x 2y²
The expression "1 x 2y²" might seem deceptively simple at first glance. However, this seemingly straightforward algebraic expression opens doors to a fascinating exploration of fundamental mathematical concepts, including variables, exponents, order of operations, and their applications in various fields. This article will dissect this expression, clarifying its meaning, exploring its potential uses, and examining its broader implications within the world of mathematics.
Introduction: Understanding the Components
Before we delve into the intricacies of 1 x 2y², let's break down its individual components. The expression consists of:
- 1: A numerical constant, the multiplicative identity. Any number multiplied by 1 remains unchanged.
- x: This represents multiplication. While often omitted (as in algebraic expressions like 2y², where the multiplication is implied), it explicitly indicates the operation being performed.
- 2: Another numerical constant.
- y: A variable, representing an unknown quantity. This can take on any numerical value.
- ²: An exponent, indicating that the variable 'y' is squared (multiplied by itself: y x y).
Therefore, the expression "1 x 2y²" signifies "1 multiplied by 2 multiplied by y squared." This can be simplified, as we'll see shortly.
Simplifying the Expression
Given the properties of multiplication (specifically the commutative and associative properties), we can rearrange and simplify the expression:
1 x 2y² = 1 x 2 x y² = 2y²
The '1' effectively disappears because multiplying any number by 1 does not change its value. Thus, the simplified and commonly used form of the expression is 2y².
Exploring the Significance of 2y²
The simplified expression, 2y², is a fundamental element in various mathematical contexts. Let's explore some of its key aspects:
-
Quadratic Functions: This expression forms the core of many quadratic functions. A quadratic function is a function of the form f(x) = ax² + bx + c, where 'a', 'b', and 'c' are constants. In our case, we have a simplified version of a quadratic function where 'a' = 2, 'b' = 0, and 'c' = 0. These functions are widely used to model parabolic trajectories, projectile motion, and optimization problems.
-
Area Calculations: Imagine a square with sides of length 'y'. The area of this square is y². Now, consider two such squares placed side-by-side. The total area would be 2y², reflecting our expression. This highlights the practical application of the expression in geometry.
-
Volume Calculations: Extending the geometric application, imagine a rectangular prism with a square base of side length 'y' and a height of 2 units. The volume of this prism is calculated as base area multiplied by height, resulting in 2y². This demonstrates the use of the expression in three-dimensional geometry.
-
Variables and Substitution: The power of 2y² lies in its generality. The variable 'y' can represent any numerical value. Substituting different values for 'y' allows us to calculate the resulting value of the expression. For instance:
- If y = 1, then 2y² = 2(1)² = 2
- If y = 2, then 2y² = 2(2)² = 8
- If y = 3, then 2y² = 2(3)² = 18
- If y = -2, then 2y² = 2(-2)² = 8 (Note: squaring a negative number results in a positive number).
-
Graphing Quadratic Functions: Plotting the expression 2y² on a graph reveals a parabola opening upwards. This parabola's vertex is located at the origin (0,0). The parabola's steepness depends on the coefficient (the number in front of the variable), in this case 2. A larger coefficient would result in a narrower parabola, and a smaller coefficient would result in a wider one.
Order of Operations (PEMDAS/BODMAS): Its Importance
While the simplicity of 1 x 2y² might seem to obviate the need for strict adherence to the order of operations, it's crucial to understand its significance in more complex algebraic expressions. The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) dictates the order in which mathematical operations should be performed. In our initial expression, the exponent (²) is applied before the multiplication. If the order were reversed, the result would be drastically different.
Advanced Applications and Extensions
The seemingly simple 2y² can serve as a building block for more complex mathematical concepts:
-
Calculus: In calculus, the expression can be used to find derivatives and integrals. The derivative of 2y² with respect to y is 4y, representing the instantaneous rate of change of the function. The integral of 2y² with respect to y is (2/3)y³ + C (where C is the constant of integration), representing the area under the curve of the function.
-
Linear Algebra: 2y² can be incorporated into matrices and vectors, forming part of linear transformations and systems of equations.
-
Differential Equations: This expression can appear in differential equations, which are equations that relate a function to its derivatives. Solving these equations often requires techniques from calculus and linear algebra.
-
Physics and Engineering: Quadratic functions, and consequently expressions like 2y², are frequently used in physics and engineering to model various phenomena, including projectile motion, the behavior of springs, and the flow of fluids.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 2y² and (2y)²?
- A: There's a significant difference. 2y² means 2 * y * y, while (2y)² means (2 * y) * (2 * y) = 4y². The parentheses dictate that the multiplication within the parentheses is performed before the squaring.
-
Q: Can 'y' be a negative number?
- A: Yes, 'y' can be any real number, including negative numbers. However, remember that when you square a negative number, the result is always positive.
-
Q: What if the expression was 1 x 2y³?
- A: This would simplify to 2y³, indicating that 'y' is cubed (y * y * y). The exponent determines the power to which the variable is raised.
Conclusion: A Foundation for Further Exploration
While seemingly simple, the expression 1 x 2y² (or its simplified form, 2y²) offers a rich introduction to core mathematical concepts. Its applications span various branches of mathematics and extend into physics, engineering, and other scientific fields. Understanding this fundamental expression lays a strong groundwork for grasping more complex algebraic concepts, including quadratic functions, calculus, and linear algebra. The journey from understanding the individual components to grasping its practical applications demonstrates the beauty and utility of even the most basic mathematical expressions. This exploration serves not only as an explanation of a simple algebraic expression but also as a springboard to a deeper understanding of the mathematical world. Further exploration into these fields will undoubtedly reveal even more intricate and fascinating uses for this seemingly simple expression.
Latest Posts
Latest Posts
-
Difference Between Emo And Gothic
Sep 16, 2025
-
Cold Blooded And Warm Blooded
Sep 16, 2025
-
The Art Of War Pdf
Sep 16, 2025
-
What Does The Fire Symbolize
Sep 16, 2025
-
Reasons For Allied Victory Ww1
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.