10 Out Of 13 Percentage
catronauts
Sep 11, 2025 · 5 min read
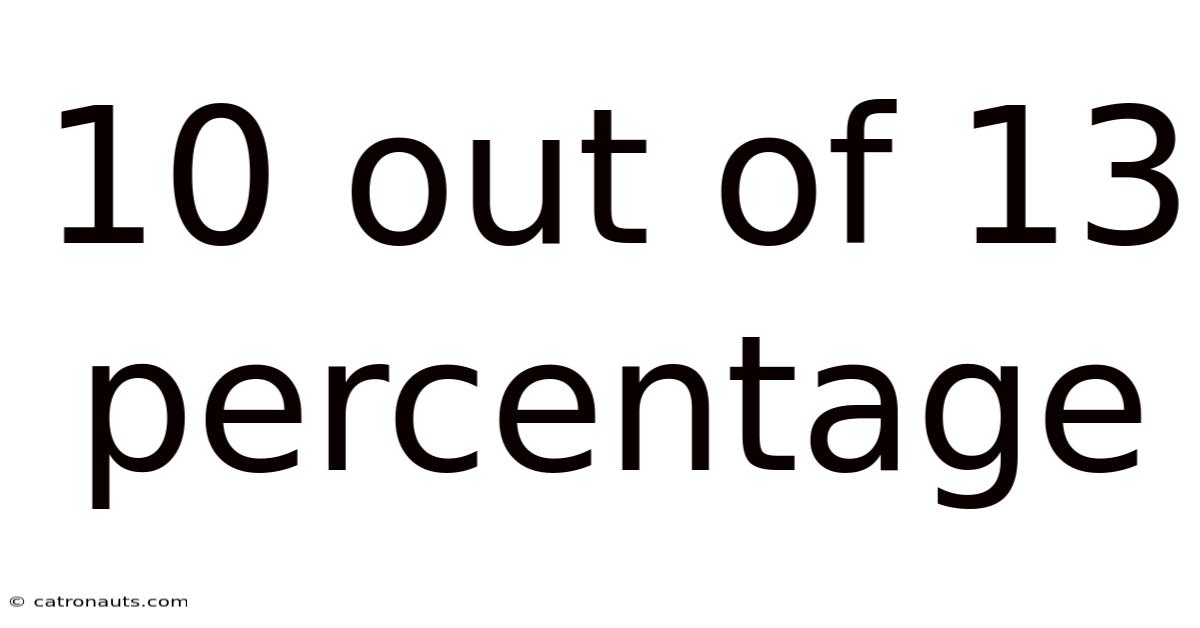
Table of Contents
Understanding and Mastering the Concept of "10 out of 13 Percentage"
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in a store to comprehending statistics in news reports. This article delves into the specific calculation of "10 out of 13 percentage," providing a step-by-step guide, exploring the underlying principles, and expanding on related concepts to solidify your grasp of percentages. We'll cover various methods, address common misconceptions, and provide examples to ensure you can confidently tackle similar problems.
What Does "10 out of 13 Percentage" Mean?
The phrase "10 out of 13 percentage" refers to expressing the fraction 10/13 as a percentage. In simpler terms, it means finding what proportion 10 represents when compared to the total of 13, and then expressing that proportion as a percentage. This type of calculation is frequently encountered in scenarios involving ratios, proportions, and statistical analysis. Mastering this calculation provides a solid foundation for understanding more complex percentage-based problems.
Calculating 10 out of 13 as a Percentage: A Step-by-Step Guide
There are two primary methods to calculate the percentage:
Method 1: Using the Fraction-to-Percentage Conversion
-
Express the given values as a fraction: The phrase "10 out of 13" directly translates into the fraction 10/13.
-
Convert the fraction to a decimal: Divide the numerator (10) by the denominator (13): 10 ÷ 13 ≈ 0.7692
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.7692 × 100 = 76.92%
Therefore, 10 out of 13 is approximately 76.92%.
Method 2: Using Proportions
This method is particularly helpful in visualizing the relationship between the parts and the whole.
-
Set up a proportion: We can express the problem as a proportion: 10/13 = x/100, where 'x' represents the percentage we want to find.
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa: 10 * 100 = 13 * x
-
Solve for x: This gives us 1000 = 13x. Divide both sides by 13: x = 1000 ÷ 13 ≈ 76.92
Therefore, using this method also yields approximately 76.92%.
Understanding the Underlying Principles
The calculation relies on the fundamental concept of ratios and proportions. A percentage is essentially a fraction where the denominator is always 100. By converting the fraction 10/13 into a decimal and then multiplying by 100, we're effectively scaling the fraction to have a denominator of 100, thereby expressing it as a percentage. The proportion method explicitly shows this scaling process.
Practical Applications and Real-World Examples
The ability to calculate percentages like "10 out of 13" has numerous practical applications in various fields:
-
Academic Performance: If a student answered 10 out of 13 questions correctly on a test, their score would be approximately 76.92%.
-
Sales and Marketing: If a salesperson made 10 sales out of 13 customer interactions, their success rate would be about 76.92%.
-
Manufacturing and Quality Control: If 10 out of 13 manufactured items pass quality checks, the pass rate is approximately 76.92%.
-
Data Analysis and Statistics: Many statistical analyses involve calculating percentages from sample data. Understanding this calculation is crucial for interpreting those results.
Addressing Common Misconceptions
A common mistake is to simply divide 13 by 10 and express the result as a percentage. This is incorrect because it reverses the ratio. Remember, the percentage represents the proportion of the numerator (10) relative to the denominator (13), not the other way around. Always ensure you are dividing the part (10) by the whole (13).
Expanding on Related Concepts
Understanding "10 out of 13 percentage" naturally leads to exploring related percentage calculations. For instance:
-
Calculating the remaining percentage: If 10 out of 13 items passed inspection, then 3 out of 13 failed (13 - 10 = 3). The failure rate would be (3/13) * 100 ≈ 23.08%. This demonstrates how the percentages of different parts of a whole sum up to 100%.
-
Working with larger numbers: The same principles apply when dealing with larger numbers. For instance, calculating "100 out of 130 percentage" uses the same method, yielding (100/130) * 100 ≈ 76.92%. The percentage remains the same because the ratio remains constant.
-
Understanding percentage change: This involves calculating the percentage increase or decrease between two values. For example, if the number of sales increased from 10 to 13, the percentage increase would be [(13-10)/10] * 100 = 30%.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage with a different numerator and denominator?
- A: The same methods apply. Simply replace 10 and 13 with your new values and follow the steps outlined above.
-
Q: How can I perform this calculation without a calculator?
- A: For approximate calculations, you can use estimation techniques. For example, 10/13 is slightly less than 10/12.5 (10/12.5 = 0.8, which is 80%). This provides a rough estimate. For precise calculations, a calculator is recommended.
-
Q: Why is the result a decimal percentage (76.92%)?
- A: The original fraction 10/13 is an irrational fraction. Its decimal equivalent does not terminate, therefore it results in a decimal percentage. You can round the result to a whole number depending on the level of precision required.
-
Q: What does the ‘approximately’ sign (≈) mean in this context?
- A: The symbol ≈ means "approximately equal to." It's used because the decimal value of 10/13 is an infinite decimal (0.7692307692...). In practical applications, we typically round the result to a suitable number of decimal places.
Conclusion
Mastering the calculation of "10 out of 13 percentage," or any similar percentage calculation, is crucial for navigating various aspects of life. By understanding the underlying principles of ratios, proportions, and fraction-to-percentage conversions, you can confidently tackle such problems and apply this knowledge to practical scenarios in academics, business, and everyday life. Remember to practice different examples and use the methods outlined above to build your confidence and skill. With consistent practice, you'll effortlessly convert fractions to percentages and accurately interpret data presented in percentage form.
Latest Posts
Latest Posts
-
Example Of A Statute Law
Sep 11, 2025
-
How Old Is Ashley Justice
Sep 11, 2025
-
Florida Age Of Sexual Consent
Sep 11, 2025
-
1 Kg How Many Grams
Sep 11, 2025
-
Dr Mrs Vandertramp French Verbs
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 13 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.