11 25 As A Percentage
catronauts
Sep 17, 2025 · 5 min read
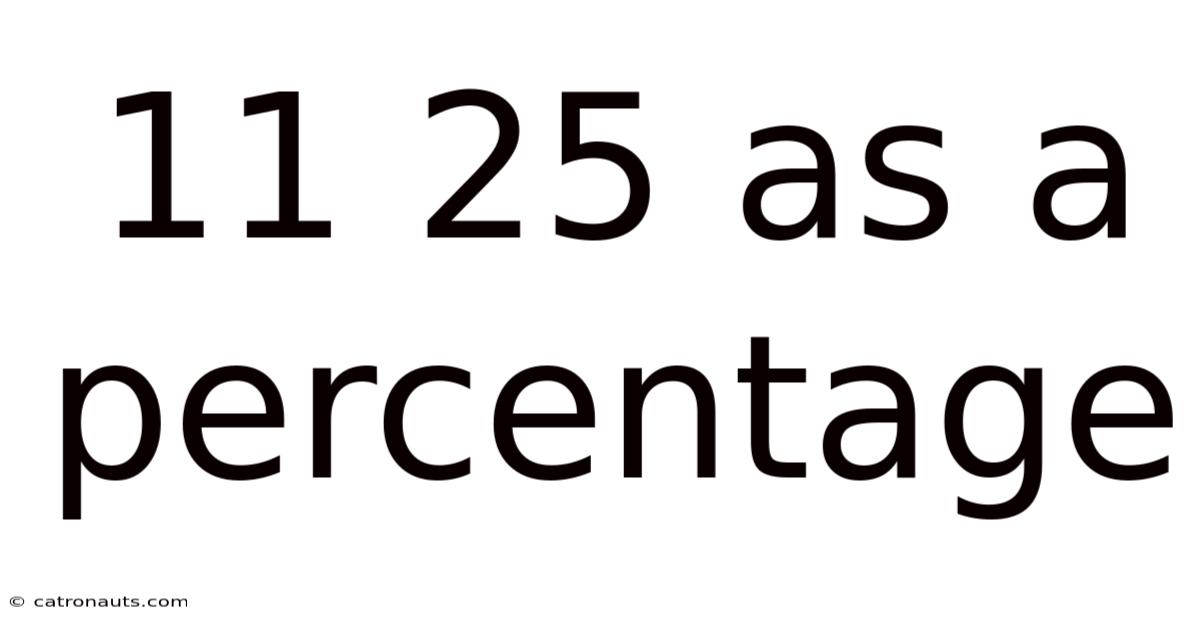
Table of Contents
Understanding 11/25 as a Percentage: A Comprehensive Guide
Representing fractions as percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax rates to understanding statistics and financial data. This article will thoroughly explore how to convert the fraction 11/25 into a percentage, explaining the process step-by-step and delving into the underlying concepts. We'll also explore different methods to achieve this conversion and examine related percentage calculations. This guide aims to provide a complete understanding of this seemingly simple yet crucial mathematical operation, suitable for learners of all levels.
Introduction: Fractions, Decimals, and Percentages
Before diving into the specific calculation of 11/25 as a percentage, let's establish a solid foundation in the relationship between fractions, decimals, and percentages. These three representational forms are fundamentally interconnected and easily interchangeable.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts, and the numerator indicates how many of those parts are being considered. For instance, 11/25 means 11 out of 25 equal parts.
A decimal is a way of expressing a number using base-ten notation, where the digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, etc.).
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
The conversion between these forms often involves division and multiplication by 100.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most common and intuitive method for converting fractions to percentages. It involves two steps:
Step 1: Convert the fraction to a decimal. To do this, we simply divide the numerator by the denominator:
11 ÷ 25 = 0.44
Step 2: Convert the decimal to a percentage. To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.44 × 100 = 44%
Therefore, 11/25 is equal to 44%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the direct relationship between percentages and fractions with a denominator of 100. The goal is to find an equivalent fraction to 11/25 that has a denominator of 100.
To achieve this, we ask ourselves: "What number, when multiplied by 25, gives 100?" The answer is 4 (25 x 4 = 100).
Since we multiply the denominator by 4, we must also multiply the numerator by 4 to maintain the equivalence of the fraction:
(11 × 4) / (25 × 4) = 44/100
Since 44/100 means 44 out of 100, this directly translates to 44%.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion where x represents the percentage we want to find:
11/25 = x/100
To solve for x, we can cross-multiply:
25x = 1100
Then, divide both sides by 25:
x = 1100/25 = 44
Therefore, x = 44%, confirming that 11/25 is equal to 44%.
Understanding the Result: What does 44% mean?
44% signifies that 11 out of 25 represents 44 parts out of 100 equal parts. It's a measure of proportion or relative size. Imagine you have 25 apples, and 11 of them are red. Then 44% of your apples are red. This percentage provides a standardized way to compare different quantities and easily understand their relative proportions.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages, and vice versa, is crucial in numerous real-world scenarios:
-
Discounts and Sales: Understanding percentages is essential for calculating discounts during sales. For example, a 20% discount on a $100 item means a reduction of $20.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating the tax amount involves multiplying the taxable amount by the tax rate.
-
Statistics and Data Analysis: Percentages are commonly used to represent data in charts, graphs, and reports. They provide an easy-to-understand way to compare different data sets and identify trends.
-
Finance: Interest rates on loans and investments are usually expressed as percentages. Understanding percentage calculations is crucial for making informed financial decisions.
-
Science: Percentages are used in many scientific calculations, such as expressing the concentration of a solution or the percentage of a certain element in a compound.
Frequently Asked Questions (FAQs)
Q1: Can I convert any fraction to a percentage?
A1: Yes, you can convert any fraction to a percentage by following the methods described above. The process involves dividing the numerator by the denominator to get a decimal, and then multiplying the decimal by 100 to obtain the percentage.
Q2: What if the decimal resulting from the fraction division is long and non-terminating (e.g., 1/3 = 0.3333...)?
A2: In such cases, you can either round the decimal to a certain number of decimal places before converting to a percentage, or express the percentage using the repeating decimal (e.g., 33.33...%). The level of precision needed depends on the context of the calculation.
Q3: Are there any online tools or calculators that can convert fractions to percentages?
A3: Yes, many online calculators are readily available that can perform this conversion automatically. Simply search for "fraction to percentage calculator" on a search engine.
Q4: Why is understanding percentages important?
A4: Understanding percentages is fundamental for interpreting and analyzing data, making financial decisions, and solving practical problems in various fields. It's a crucial skill for everyday life and many professional fields.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages, as demonstrated with the example of 11/25, is a straightforward process with multiple approaches. Mastering this skill empowers you to confidently handle various mathematical problems and real-world scenarios that involve proportions and relative quantities. By understanding the underlying principles and employing the methods discussed in this article, you can easily convert any fraction into a percentage and improve your overall mathematical literacy. Remember to practice regularly to build fluency and confidence in handling percentage calculations. This skill is not only valuable for academic success but also essential for navigating the complexities of everyday life and professional environments.
Latest Posts
Latest Posts
-
Alice In The Wonderland Makeup
Sep 17, 2025
-
Aqua In French Google Translate
Sep 17, 2025
-
Author Of Little Red Hen
Sep 17, 2025
-
Sir Francis Drake Motel Reviews
Sep 17, 2025
-
What Is An Unconditional Discharge
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 11 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.