12 25 As A Percentage
catronauts
Sep 14, 2025 · 5 min read
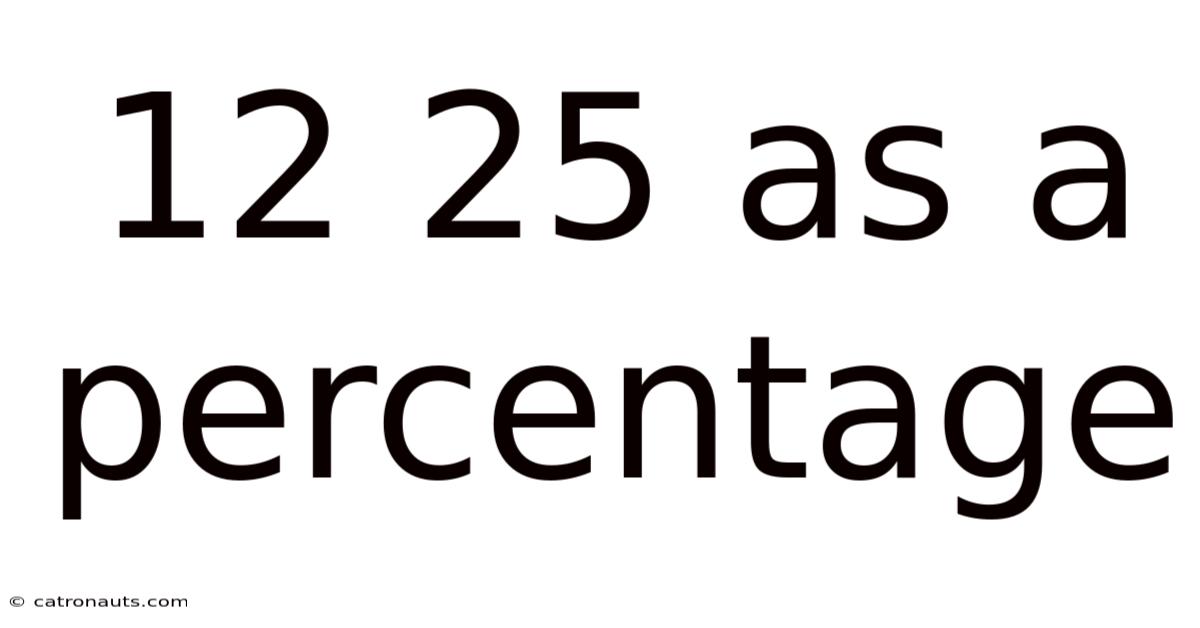
Table of Contents
12/25 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications in daily life, from calculating discounts to understanding financial reports. This comprehensive guide will explore the conversion of the fraction 12/25 into a percentage, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also cover common applications and address frequently asked questions to ensure a thorough understanding.
Introduction: Understanding Fractions and Percentages
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The fraction 12/25 means 12 parts out of a total of 25 parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It indicates how many parts out of 100 constitute a particular portion of a whole. For instance, 50% means 50 parts out of 100, which is equivalent to 1/2 or 0.5.
Converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100, then expressing this fraction as a percentage.
Steps to Convert 12/25 to a Percentage
There are two primary methods to convert 12/25 to a percentage:
Method 1: Finding an Equivalent Fraction with a Denominator of 100
- Identify the denominator: Our denominator is 25.
- Find the multiplying factor: To change the denominator from 25 to 100, we need to multiply it by 4 (because 100 / 25 = 4).
- Multiply both the numerator and the denominator: To maintain the fraction's value, we must multiply both the numerator and the denominator by the same factor. So, we multiply 12/25 by 4/4: (12 * 4) / (25 * 4) = 48/100
- Express as a percentage: A fraction with a denominator of 100 can be directly written as a percentage. Therefore, 48/100 is equivalent to 48%.
Method 2: Using Decimal Conversion
- Convert the fraction to a decimal: Divide the numerator (12) by the denominator (25): 12 ÷ 25 = 0.48
- Multiply by 100: To convert the decimal to a percentage, multiply the decimal by 100: 0.48 * 100 = 48
- Add the percentage symbol: Finally, add the percentage symbol to indicate that the result is a percentage: 48%
The Mathematical Explanation Behind the Conversion
The conversion from a fraction to a percentage relies on the fundamental concept of equivalent fractions. Multiplying both the numerator and the denominator of a fraction by the same non-zero number does not change the value of the fraction. This principle is used to create an equivalent fraction with a denominator of 100, which directly translates to a percentage.
The decimal conversion method uses the fact that a percentage is essentially a decimal multiplied by 100. Dividing the numerator by the denominator gives the decimal representation of the fraction. Multiplying this decimal by 100 converts it into its percentage equivalent.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
- Financial Calculations: Calculating interest rates, discounts, tax rates, profit margins, and investment returns all involve percentage calculations. For example, if a store offers a 48% discount on an item, you can use this knowledge to easily calculate the final price.
- Data Analysis: Percentages are widely used to represent data in graphs, charts, and reports. They provide an easy-to-understand way to compare different proportions or changes over time.
- Academic Assessments: Grades and scores in academic assessments are often expressed as percentages. Understanding percentages helps you gauge your performance and progress.
- Scientific Studies: Percentages are used in scientific studies to express the frequency of events, the proportion of a population with a certain characteristic, and to analyze experimental results.
- Everyday Life: Calculating tips in restaurants, determining sale prices, and understanding statistics in news reports all necessitate a grasp of percentages.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, you can convert any fraction to a percentage using the methods described above. However, for fractions with very large denominators, the decimal conversion method might be more efficient.
Q2: What if the fraction results in a repeating decimal?
A2: If the division results in a repeating decimal (e.g., 1/3 = 0.333...), you can round the decimal to a suitable number of decimal places before multiplying by 100. For example, you could round 0.333... to 0.33 and then multiply by 100 to get 33%.
Q3: Is there a quicker way to calculate percentages mentally?
A3: For some common fractions, mental shortcuts exist. For example, you can quickly recognize that 1/4 is 25%, 1/2 is 50%, and 3/4 is 75%. With practice, you can develop intuition for other fractions as well.
Q4: What if I have a mixed number (e.g., 1 12/25)?
A4: First, convert the mixed number into an improper fraction. For example, 1 12/25 becomes (25 + 12)/25 = 37/25. Then, follow either of the methods described above to convert this improper fraction to a percentage.
Q5: Are there any online tools to help with percentage calculations?
A5: While this document avoids external links, numerous online calculators and conversion tools are available to assist with percentage calculations, especially for more complex scenarios.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a valuable skill with wide-ranging applications. By understanding the underlying mathematical principles and applying the step-by-step methods outlined in this guide, you can confidently convert any fraction to a percentage and effectively utilize this knowledge in various aspects of your life. Remember, practice makes perfect, so try converting different fractions to reinforce your understanding. With consistent practice, you'll become proficient in this fundamental mathematical skill. From simple everyday tasks to complex financial calculations, your ability to work with percentages will prove to be a significant asset. Don't hesitate to revisit these steps and examples whenever you need a refresher, and remember that the key is understanding the process, not just memorizing the steps.
Latest Posts
Latest Posts
-
2 5 As A Number
Sep 14, 2025
-
20 30 As A Percentage
Sep 14, 2025
-
Insects That Look Like Ticks
Sep 14, 2025
-
Dimensions Of Mona Lisa Painting
Sep 14, 2025
-
Food Chain With A Snake
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 12 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.