15 24 As A Decimal
catronauts
Sep 12, 2025 · 5 min read
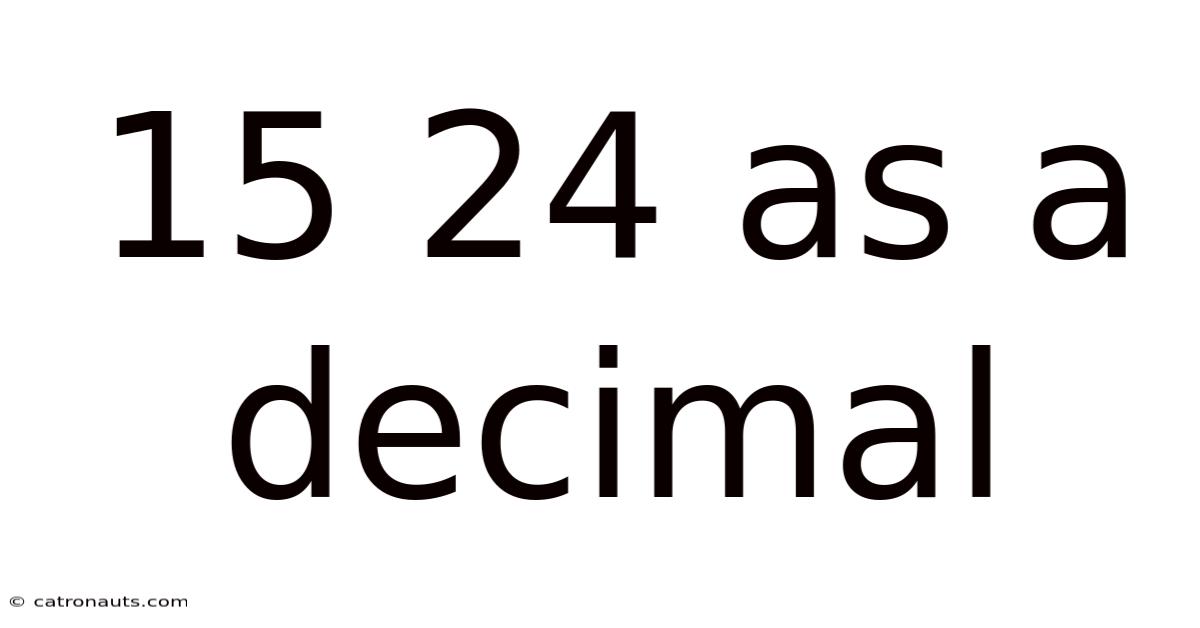
Table of Contents
15/24 as a Decimal: A Comprehensive Guide to Fraction Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the fraction 15/24 to its decimal equivalent, exploring various methods and delving into the underlying mathematical principles. We'll also address common misconceptions and provide practical applications to solidify your understanding. This guide is perfect for students, educators, and anyone looking to refresh their knowledge of fraction-to-decimal conversions.
Understanding Fractions and Decimals
Before diving into the conversion of 15/24, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a part of a whole using a base-ten system, with a decimal point separating the whole number part from the fractional part.
For example, the fraction 1/2 represents one out of two equal parts, while its decimal equivalent is 0.5. The fraction 3/4 represents three out of four equal parts, with a decimal equivalent of 0.75. The key to converting fractions to decimals lies in understanding that the denominator represents the power of ten used to express the fraction in decimal form.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. In this method, we divide the numerator (15) by the denominator (24).
-
Set up the division: Write 15 as the dividend (inside the division symbol) and 24 as the divisor (outside the division symbol).
-
Add a decimal point and zeros: Since 15 is smaller than 24, we add a decimal point to the dividend and append zeros as needed. This doesn't change the value of the number, it just allows us to continue the division.
-
Perform the division: Perform the long division step by step. You'll find that 24 goes into 150 six times (24 x 6 = 144). Subtract 144 from 150, leaving a remainder of 6. Bring down another zero to get 60. 24 goes into 60 two times (24 x 2 = 48). Subtract 48 from 60, leaving a remainder of 12. Bring down another zero to get 120. 24 goes into 120 five times (24 x 5 = 120). The remainder is 0, indicating the division is complete.
Therefore, 15 ÷ 24 = 0.625
Method 2: Simplifying the Fraction
Before performing long division, it's often beneficial to simplify the fraction. This makes the long division process easier and less prone to errors. We can simplify 15/24 by finding the greatest common divisor (GCD) of 15 and 24. The GCD of 15 and 24 is 3. Dividing both the numerator and denominator by 3, we get:
15 ÷ 3 = 5 24 ÷ 3 = 8
So, the simplified fraction is 5/8. Now, we can perform the long division using 5/8:
5 ÷ 8 = 0.625
This demonstrates that simplifying the fraction first can streamline the conversion process.
Method 3: Converting to an Equivalent Fraction with a Denominator of a Power of 10
While less practical for 15/24, this method is useful for fractions with denominators that can be easily converted to powers of 10 (10, 100, 1000, etc.). Unfortunately, 24 cannot be easily converted to a power of 10. However, understanding this method is important for certain types of fraction conversions. If we could find a multiplier to turn the denominator into a power of 10, we'd simply multiply both the numerator and denominator by that multiplier and then express the fraction as a decimal.
Understanding the Decimal Result: 0.625
The decimal equivalent of 15/24 (or 5/8) is 0.625. This means that 15/24 represents 625 out of 1000 equal parts. It can also be expressed as 62.5% (percentage).
Recurring Decimals: A Quick Note
Not all fractions convert to terminating decimals like 0.625. Some fractions result in recurring decimals, where one or more digits repeat infinitely. For example, 1/3 converts to 0.3333... (the 3 repeats infinitely). Understanding the difference between terminating and recurring decimals is crucial for working with fractions and decimals effectively.
Practical Applications of Fraction-to-Decimal Conversions
Converting fractions to decimals is essential in various fields, including:
- Finance: Calculating percentages, interest rates, and discounts.
- Engineering: Precision measurements and calculations.
- Science: Data analysis and representation.
- Everyday Life: Cooking, measuring, and dividing quantities.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to convert 15/24 to a decimal? A: Yes, most calculators have a fraction-to-decimal conversion function. Simply enter 15/24 and press the equals button.
-
Q: What if I get a remainder after long division? A: If you have a non-zero remainder after long division, it means the decimal is either recurring or you need to continue the division by adding more zeros to the dividend.
-
Q: Why is simplifying the fraction helpful? A: Simplifying reduces the size of the numbers involved in long division, making the calculation easier and less error-prone.
-
Q: Are there any other methods to convert fractions to decimals? A: While long division and simplification are the most common methods, other techniques exist, particularly when dealing with fractions whose denominators are easily converted to powers of 10.
Conclusion
Converting the fraction 15/24 to its decimal equivalent, 0.625, involves a straightforward process. The methods described above – long division and simplifying the fraction – provide clear and efficient ways to achieve this conversion. Understanding these methods is crucial for mastering fundamental mathematical concepts and applying them to various practical scenarios. Remember to practice regularly to enhance your skills and build confidence in your ability to convert fractions to decimals accurately and efficiently. The ability to confidently work with fractions and decimals is a cornerstone of mathematical fluency and opens doors to more advanced mathematical concepts. Don't hesitate to revisit these methods and practice converting various fractions to decimals to solidify your understanding.
Latest Posts
Latest Posts
-
Tales Of The Arabian Nights
Sep 12, 2025
-
How Many Ounces 1 Liter
Sep 12, 2025
-
How Did Willem Jansz Die
Sep 12, 2025
-
Food Web For A Tundra
Sep 12, 2025
-
How To Draw And Ellipse
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 15 24 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.