15 Percent As A Fraction
catronauts
Sep 14, 2025 · 5 min read
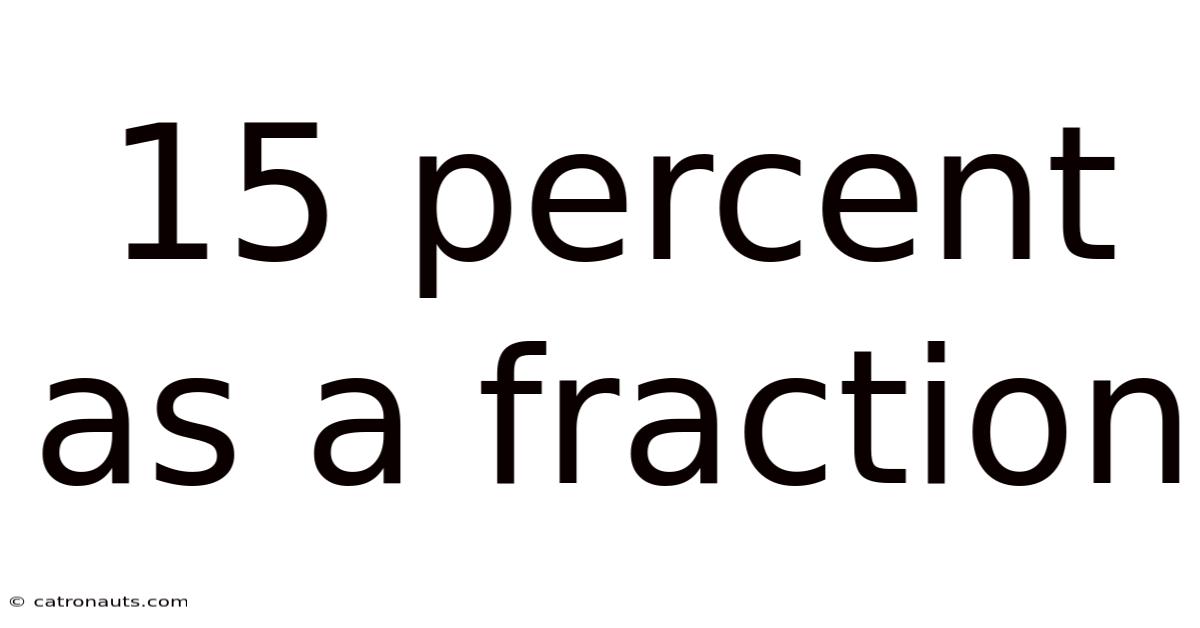
Table of Contents
15 Percent as a Fraction: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life calculations. This article delves into the seemingly simple concept of representing 15 percent as a fraction, exploring the process, underlying principles, and practical applications. We'll move beyond the basic conversion and explore how to simplify fractions, handle different scenarios, and even delve into the deeper mathematical concepts involved. This detailed guide aims to provide a thorough understanding for students and anyone looking to solidify their grasp of percentage-to-fraction conversions.
Understanding Percentages and Fractions
Before diving into the conversion of 15 percent to a fraction, let's clarify the fundamental concepts. A percentage represents a fraction of 100. The word "percent" literally means "per hundred" ( per centum in Latin). Therefore, 15 percent means 15 out of 100.
A fraction, on the other hand, expresses a part of a whole. It's written as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, and the numerator indicates how many of those parts are being considered.
Converting 15 Percent to a Fraction: The Basic Approach
The conversion of 15% to a fraction is straightforward:
-
Write the percentage as a fraction with a denominator of 100: 15% can be written as 15/100. This directly reflects the definition of percentage – 15 parts out of 100 total parts.
-
Simplify the fraction (if possible): Both 15 and 100 are divisible by 5. Dividing both the numerator and the denominator by 5, we get:
15 ÷ 5 = 3 100 ÷ 5 = 20
Therefore, the simplified fraction is 3/20.
This simplified fraction, 3/20, is the most concise and accurate representation of 15% as a fraction. It maintains the same proportional value as 15/100 but is expressed in its lowest terms.
Why Simplify Fractions?
Simplifying fractions is crucial for several reasons:
-
Clarity and Conciseness: A simplified fraction is easier to understand and work with compared to a more complex, unsimplified version. 3/20 is more readily grasped than 15/100.
-
Easier Calculations: Simplified fractions make subsequent calculations (like addition, subtraction, multiplication, and division) simpler and less prone to errors.
-
Standard Form: In mathematics, presenting fractions in their simplest form is considered standard practice and enhances the clarity and professionalism of your work.
-
Identifying Equivalency: Simplifying fractions helps to easily identify equivalent fractions. For example, recognizing that 15/100, 30/200, and 75/500 all simplify to 3/20 highlights their equivalence.
Different Scenarios and Applications
The conversion of 15% to a fraction finds applications in many real-world scenarios. Let's explore a few examples:
-
Calculating Discounts: If a store offers a 15% discount on an item, you can use the fraction 3/20 to quickly calculate the discount amount. For instance, on a $100 item, the discount would be (3/20) * $100 = $15.
-
Determining Proportions: In recipes, understanding proportions is vital. If a recipe calls for 15% of a total ingredient weight to be a certain spice, the fraction 3/20 provides a convenient way to calculate the required amount.
-
Statistical Analysis: In statistical analysis, percentages are often converted to fractions to simplify calculations and comparisons. Representing data as fractions can provide a clearer picture of the relationships between different data points.
-
Financial Calculations: Interest rates, tax calculations, and profit margins frequently involve percentages, and converting them to fractions can simplify the calculations considerably. Understanding 15% as 3/20 allows for quicker mental calculations in many financial scenarios.
Mathematical Explanation: Prime Factorization
The simplification of the fraction 15/100 can be further understood through prime factorization. Prime factorization is the process of breaking down a number into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 15: 3 x 5
- Prime factorization of 100: 2 x 2 x 5 x 5 (or 2² x 5²)
The fraction 15/100 can therefore be written as (3 x 5) / (2² x 5²). Notice that there is a common factor of 5 in both the numerator and denominator. Canceling this common factor results in 3 / (2² x 5) = 3/20.
Converting Other Percentages to Fractions
The process for converting other percentages to fractions follows the same steps:
- Write the percentage as a fraction with a denominator of 100.
- Simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
For example:
- 25%: 25/100 simplifies to 1/4
- 50%: 50/100 simplifies to 1/2
- 75%: 75/100 simplifies to 3/4
- 10%: 10/100 simplifies to 1/10
- 20%: 20/100 simplifies to 1/5
Frequently Asked Questions (FAQ)
Q: Can I express 15% as a decimal?
A: Yes, 15% is equivalent to 0.15. To convert a percentage to a decimal, simply divide the percentage by 100. This is because percentages are based on 100.
Q: What if the fraction doesn't simplify?
A: If the numerator and denominator of the fraction share no common factors other than 1, the fraction is already in its simplest form. For example, 17/100 cannot be simplified further.
Q: Are there different ways to express 15%?
A: While 3/20 is the simplest form, you could express it as equivalent fractions such as 6/40, 9/60, 12/80, and so on. However, these are less concise and efficient than 3/20.
Q: How do I convert a fraction back to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100. For example, 3/20 = 0.15 x 100 = 15%.
Conclusion
Converting 15 percent to a fraction, resulting in the simplified fraction 3/20, is a fundamental mathematical skill with far-reaching applications. This detailed guide has explored the process, the reasons behind simplification, and various real-world scenarios where this conversion proves valuable. By understanding the underlying principles and practicing these conversions, you can significantly improve your mathematical proficiency and problem-solving abilities across numerous fields. Remember, the key is to master the process of simplification to ensure clarity, accuracy, and efficiency in your calculations.
Latest Posts
Latest Posts
-
Charge On A Silver Ion
Sep 15, 2025
-
What Is The Price Mechanism
Sep 15, 2025
-
What Does A Penguin Eat
Sep 15, 2025
-
Multiply Whole Numbers With Decimals
Sep 15, 2025
-
Characteristics Of Labor In Economics
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.