15 Percent In A Fraction
catronauts
Sep 18, 2025 · 5 min read
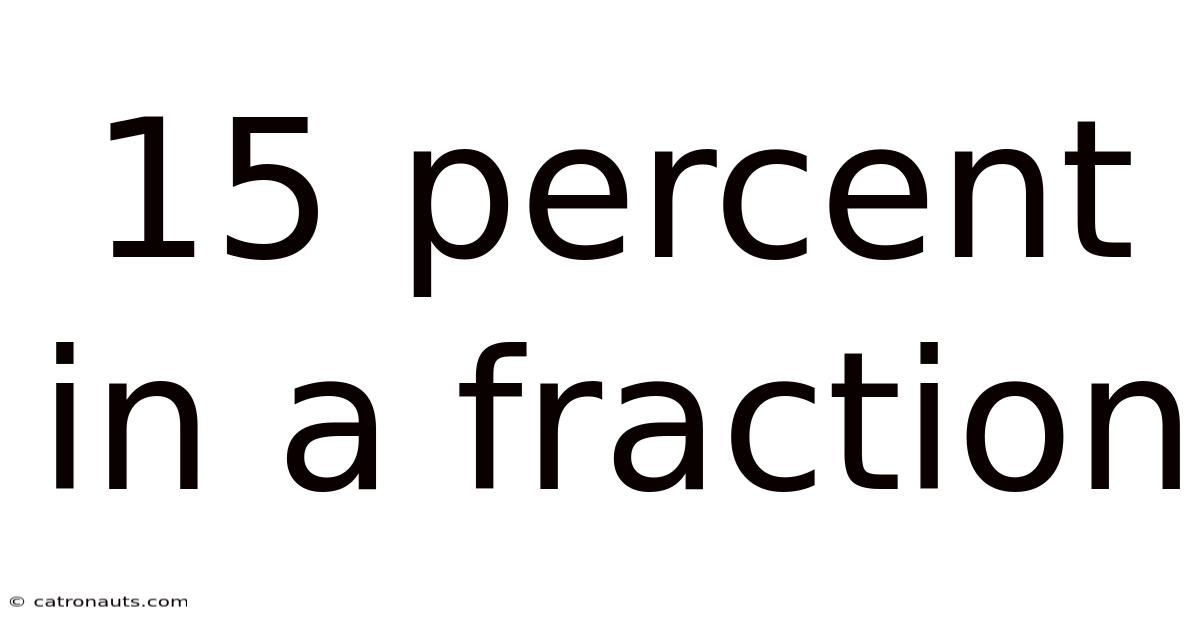
Table of Contents
15 Percent: Understanding Fractions, Decimals, and Percentages
Representing parts of a whole is fundamental to mathematics and everyday life. Whether you're calculating discounts, understanding financial reports, or tackling complex equations, grasping the relationship between fractions, decimals, and percentages is crucial. This comprehensive guide will delve into the intricacies of 15 percent, explaining its representation as a fraction, decimal, and exploring its applications in various contexts. We'll also clarify common misconceptions and provide practical examples to solidify your understanding.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the specifics of 15 percent, let's refresh our understanding of the three core concepts:
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, 1/2 represents one part out of two equal parts.
-
Decimals: Decimals are another way to represent parts of a whole, using a base-ten system. The decimal point separates the whole number from the fractional part. For example, 0.5 is equivalent to 1/2.
-
Percentages: Percentages represent parts of a whole as a fraction of 100. The symbol "%" signifies "per hundred." For example, 50% means 50 parts out of 100, which is equivalent to 1/2 or 0.5.
Converting 15 Percent to a Fraction
To convert 15 percent to a fraction, we remember that "percent" means "per hundred." Therefore, 15% can be written as the fraction 15/100.
This fraction can be simplified by finding the greatest common divisor (GCD) of 15 and 100, which is 5. Dividing both the numerator and the denominator by 5, we get:
15/100 = (15 ÷ 5) / (100 ÷ 5) = 3/20
Therefore, 15% is equivalent to the fraction 3/20.
Converting 15 Percent to a Decimal
Converting a percentage to a decimal involves dividing the percentage by 100. For 15%, this is:
15% ÷ 100 = 0.15
Therefore, 15% is equivalent to the decimal 0.15. This is easily achieved by moving the decimal point two places to the left.
Real-World Applications of 15 Percent
Understanding 15% as a fraction and decimal allows us to apply it in various real-world scenarios:
- Discounts: A 15% discount on a $100 item means you save 15% of $100. Using the decimal form, this is:
0.15 * $100 = $15
You would pay $100 - $15 = $85. Using the fraction, this would be:
(3/20) * $100 = $15
- Taxes: If a sales tax is 15%, the calculation is similar. On a $50 item, the tax would be:
0.15 * $50 = $7.50
The total cost would be $50 + $7.50 = $57.50
- Tips: Calculating a 15% tip on a restaurant bill follows the same principle. On a $60 bill, a 15% tip would be:
0.15 * $60 = $9
-
Interest Rates: 15% interest on a loan or investment is calculated similarly, although the specific calculation depends on whether it is simple or compound interest.
-
Statistics and Probability: 15% can represent a proportion or probability in various statistical contexts. For instance, if 15% of a population has a particular characteristic, this translates to 3 out of every 20 individuals.
-
Proportional Reasoning: Understanding 15% as 3/20 allows for efficient proportional reasoning. For example, if 3 out of 20 apples are rotten, this represents 15% of the apples.
Working with 15% in Different Contexts
Let's examine more complex scenarios involving 15%:
Scenario 1: Finding the original price after a discount
You bought an item for $85 after a 15% discount. What was the original price?
Let 'x' be the original price. The discounted price is 85% of the original price (100% - 15% = 85%). Therefore:
0.85x = $85
x = $85 / 0.85 = $100
The original price was $100.
Scenario 2: Calculating percentage increase
Your salary increased by 15% to $69,000. What was your original salary?
Let 'y' be your original salary. Your new salary is 115% of your original salary (100% + 15% = 115%).
1.15y = $69,000
y = $69,000 / 1.15 = $60,000
Your original salary was $60,000.
Scenario 3: Comparing percentages
If you have two discounts – 15% and 20% – which is better? The 20% discount is always better, as it represents a larger reduction in price.
Common Misconceptions about Percentages
Several misconceptions often arise when working with percentages:
-
Adding percentages directly: You cannot simply add percentages together unless they refer to the same base value. For example, a 15% increase followed by a 15% decrease does not result in the original value.
-
Incorrect rounding: Always consider significant figures and appropriate rounding procedures when working with percentages, especially in financial calculations.
-
Confusing percentage change with absolute change: A 15% increase on a small number results in a smaller absolute increase than a 15% increase on a large number.
Frequently Asked Questions (FAQ)
Q: How do I calculate 15% of a number quickly in my head?
A: You can approximate 15% by calculating 10% (easy to find by moving the decimal point one place to the left) and then adding half of that amount (5%). For example, 15% of 80 is approximately 8 (10%) + 4 (5%) = 12.
Q: What is the inverse of 15%?
A: The inverse of finding 15% of a number is finding what number 15% represents. This often involves solving an equation, as shown in the scenarios above.
Q: Can I use a calculator to find 15% of a number?
A: Yes, simply multiply the number by 0.15.
Q: How does 15% relate to other percentages?
A: 15% is one-sixth of 90%, one-third of 45%, and one-fifth of 75%.
Conclusion
Understanding 15 percent, whether as a fraction (3/20) or a decimal (0.15), is a valuable skill applicable across numerous contexts. Mastering these conversions and their applications allows for accurate calculations in various fields, from finance and business to statistics and everyday life. By carefully considering the context and avoiding common misconceptions, you can confidently work with percentages to solve problems and make informed decisions. Remember to always double-check your work and use appropriate rounding techniques to ensure accuracy. The ability to easily manipulate fractions, decimals, and percentages is a cornerstone of mathematical literacy and a valuable tool in many areas of life.
Latest Posts
Latest Posts
-
Flight Time Korea To Japan
Sep 18, 2025
-
Saturated Hydrocarbon Vs Unsaturated Hydrocarbon
Sep 18, 2025
-
What Is 30 Of 30
Sep 18, 2025
-
Books Written By Emily Bronte
Sep 18, 2025
-
Lewis Dot Structure For Nitrogen
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.