16 20 As A Percent
catronauts
Sep 13, 2025 · 5 min read
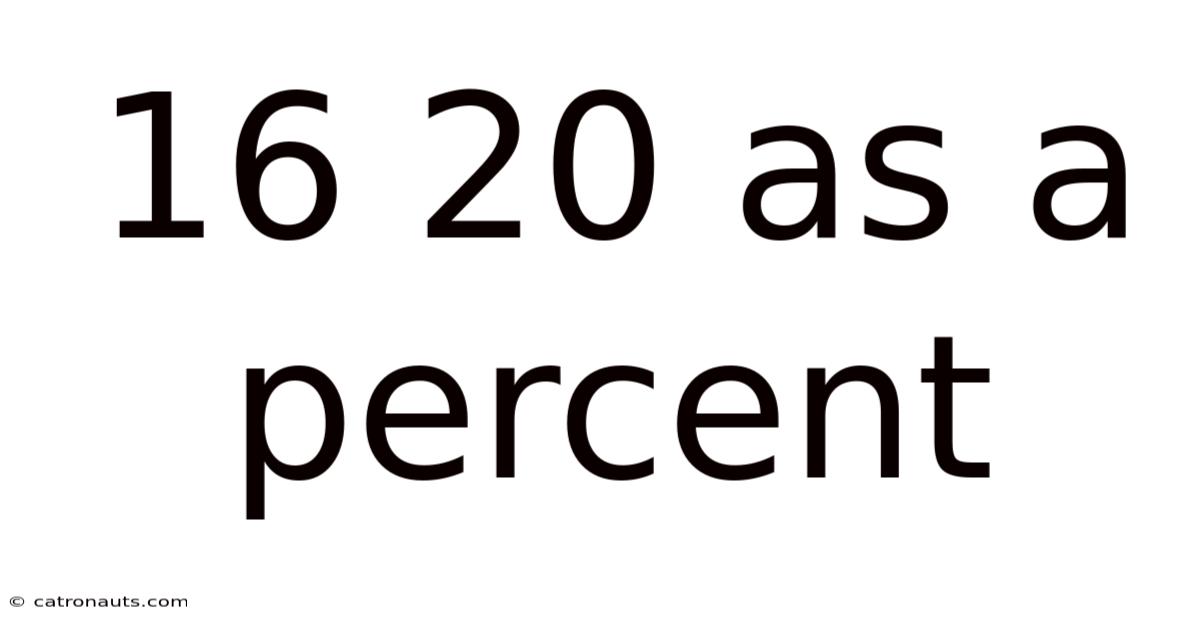
Table of Contents
Understanding 16 out of 20 as a Percentage: A Comprehensive Guide
Many everyday situations require us to understand fractions and convert them into percentages. Knowing how to calculate percentages is crucial for various applications, from calculating grades to understanding financial reports, and even comparing sale discounts. This article will thoroughly explain how to calculate 16 out of 20 as a percentage, providing a step-by-step guide and exploring the underlying mathematical concepts. We'll also delve into practical applications and address frequently asked questions, ensuring you gain a comprehensive understanding of this essential mathematical skill.
Understanding Fractions and Percentages
Before diving into the calculation, let's clarify the fundamental concepts involved. A fraction represents a part of a whole. In this case, "16 out of 20" is a fraction, where 16 is the numerator (the part) and 20 is the denominator (the whole).
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts out of 100 comprise the whole. For example, 50% means 50 out of 100, or one-half. Converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100, or using a simpler calculation method.
Calculating 16 out of 20 as a Percentage: Step-by-Step Guide
There are two primary ways to calculate 16 out of 20 as a percentage:
Method 1: Using the Fraction Method
-
Express the fraction: Write the given information as a fraction: 16/20.
-
Convert to a decimal: Divide the numerator (16) by the denominator (20): 16 ÷ 20 = 0.8
-
Convert to a percentage: Multiply the decimal by 100: 0.8 × 100 = 80
-
Add the percentage symbol: The result is 80%.
Therefore, 16 out of 20 is equal to 80%.
Method 2: Using the Proportion Method
This method involves setting up a proportion to find the equivalent percentage.
-
Set up a proportion: We want to find the percentage 'x' that represents 16 out of 20. We can set up the proportion: 16/20 = x/100
-
Cross-multiply: To solve for x, cross-multiply: 16 × 100 = 20 × x This simplifies to 1600 = 20x
-
Solve for x: Divide both sides by 20: 1600 ÷ 20 = x This gives us x = 80
-
Add the percentage symbol: Therefore, x = 80%, confirming that 16 out of 20 is 80%.
Understanding the Mathematical Concept: Ratio and Proportion
The calculation of percentages fundamentally involves understanding ratios and proportions. A ratio compares two quantities, while a proportion states that two ratios are equal. In our example, the ratio of 16 to 20 is equivalent to the ratio of 80 to 100 (80%). This equivalence is what allows us to convert fractions to percentages.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages is crucial in many real-world scenarios:
-
Academic Performance: Calculating grades based on correct answers out of the total number of questions. For instance, scoring 16 out of 20 on a test translates to an 80% grade.
-
Financial Calculations: Determining interest rates, discounts, tax rates, and profit margins. Understanding percentages is essential for budgeting and managing finances effectively.
-
Data Analysis: Interpreting statistical data, such as survey results or market research findings. Representing data as percentages makes it easier to visualize and compare different data sets.
-
Sales and Marketing: Calculating discounts, markups, and sales growth. Companies use percentages to advertise deals and measure their marketing success.
-
Everyday Life: Calculating tips in restaurants, understanding sale discounts, or comparing prices. Percentages are integrated into many aspects of daily life.
Beyond 16 out of 20: A Broader Perspective
While this article focuses on calculating 16 out of 20 as a percentage, the methods discussed are applicable to any fraction. To calculate any fraction as a percentage, simply follow the steps outlined above: convert the fraction to a decimal by dividing the numerator by the denominator, and then multiply the decimal by 100 to obtain the percentage.
Advanced Concepts: Percentage Increase and Decrease
Understanding percentages extends beyond simple conversions. We often encounter scenarios involving percentage increases or decreases:
-
Percentage Increase: This calculates the percentage change when a quantity increases. For example, if a price increases from $20 to $24, the percentage increase is calculated as: [(24-20)/20] × 100 = 20%.
-
Percentage Decrease: This calculates the percentage change when a quantity decreases. If a price decreases from $20 to $16, the percentage decrease is calculated as: [(20-16)/20] × 100 = 20%.
Frequently Asked Questions (FAQs)
Q1: What if the denominator is not easily divisible by 100?
A1: If the denominator isn't easily divisible by 100, simply divide the numerator by the denominator to obtain the decimal, and then multiply the decimal by 100. You might end up with a percentage that includes decimal places.
Q2: How can I check my percentage calculation?
A2: You can check your calculation by reversing the process. Convert the percentage back to a decimal (divide by 100) and then multiply by the original denominator. The result should be the original numerator.
Q3: Are there any online calculators to help with percentage calculations?
A3: Yes, many online calculators are available to simplify percentage calculations. These calculators can handle various types of percentage problems, including those involving increases and decreases. However, understanding the underlying principles is still crucial for problem-solving.
Q4: What are some common mistakes to avoid when calculating percentages?
A4: Some common mistakes include incorrect placement of the decimal point, forgetting to multiply by 100, and misinterpreting the context of the problem. Carefully review the problem and double-check your calculations to minimize errors.
Conclusion
Converting 16 out of 20 to a percentage (80%) is a straightforward process involving simple arithmetic. However, understanding the underlying mathematical concepts of fractions, decimals, ratios, and proportions provides a solid foundation for tackling more complex percentage problems. The ability to calculate percentages is a valuable skill applicable across various domains, making it an essential tool for academic success, financial literacy, and everyday life. By mastering these techniques, you will enhance your mathematical proficiency and gain a deeper understanding of the world around you.
Latest Posts
Latest Posts
-
How Long Is 109 Minutes
Sep 13, 2025
-
Dance Dance Dance Haruki Murakami
Sep 13, 2025
-
Double 1 3 4 Cup
Sep 13, 2025
-
Example Of A Pull Factor
Sep 13, 2025
-
Chomsky Who Rules The World
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 16 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.