18 60 As A Percentage
catronauts
Sep 12, 2025 · 5 min read
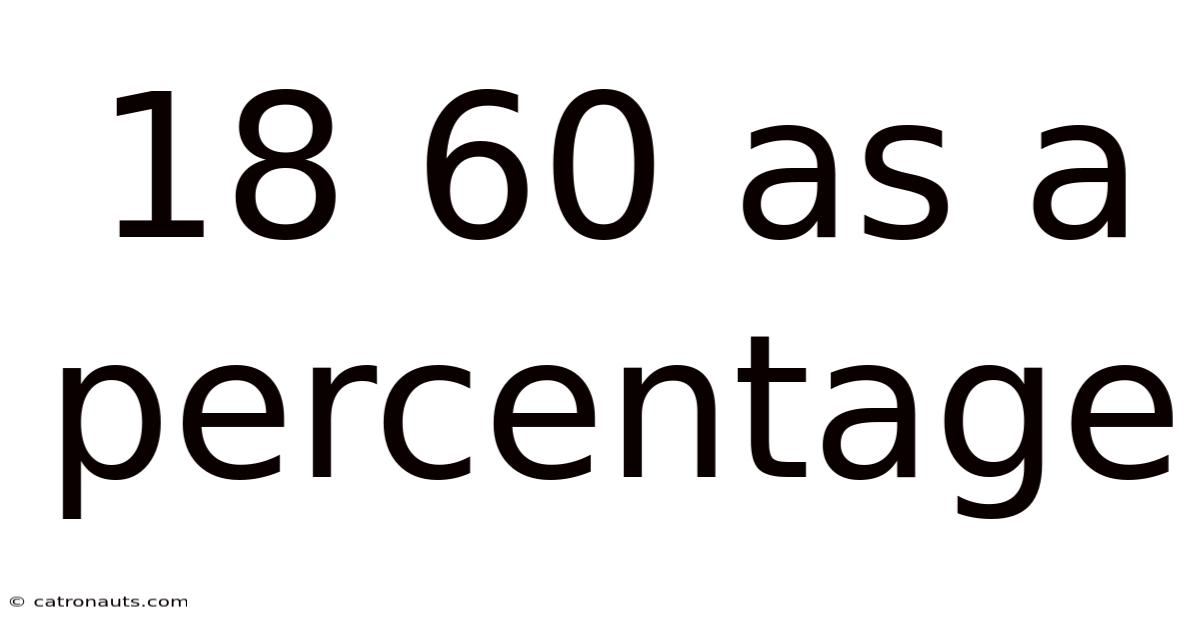
Table of Contents
18/60 as a Percentage: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications across various fields, from everyday budgeting to complex scientific calculations. This article will delve deep into converting the fraction 18/60 into a percentage, explaining the process step-by-step, providing alternative methods, and exploring the broader context of percentage calculations. We'll also address frequently asked questions and offer practical examples to solidify your understanding. By the end, you'll not only know the answer but also possess a solid grasp of the underlying principles.
Introduction: Understanding Fractions and Percentages
Before we dive into the specifics of converting 18/60, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 18/60, 18 is the numerator and 60 is the denominator. This means we have 18 parts out of a total of 60 parts.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" is used to denote percentage. Essentially, a percentage shows the proportion of a quantity relative to 100. For instance, 50% means 50 out of 100, or one-half.
Method 1: Converting 18/60 to a Percentage Directly
The most straightforward method to convert 18/60 to a percentage involves two simple steps:
-
Divide the numerator by the denominator: Divide 18 by 60. This gives us 0.3.
-
Multiply the result by 100: Multiply 0.3 by 100. This yields 30.
Therefore, 18/60 is equal to 30%.
Method 2: Simplifying the Fraction Before Conversion
Often, simplifying the fraction before converting to a percentage makes the calculation easier. This is particularly useful when dealing with larger numbers. To simplify 18/60, we find the greatest common divisor (GCD) of 18 and 60, which is 6. We then divide both the numerator and the denominator by the GCD:
18 ÷ 6 = 3 60 ÷ 6 = 10
This simplifies the fraction to 3/10. Now, we can convert 3/10 to a percentage:
-
Divide the numerator by the denominator: 3 ÷ 10 = 0.3
-
Multiply the result by 100: 0.3 × 100 = 30
Again, we arrive at the answer: 30%.
Method 3: Using Proportions
Another approach is to use proportions. We set up a proportion where x represents the percentage we're trying to find:
18/60 = x/100
To solve for x, we cross-multiply:
60x = 1800
Then, we divide both sides by 60:
x = 1800 ÷ 60 = 30
So, 18/60 is equal to 30%.
The Mathematical Explanation: Why This Works
The core principle behind these methods lies in the definition of a percentage. A percentage is a fraction with a denominator of 100. When we divide the numerator of a fraction by the denominator and multiply by 100, we're essentially scaling the fraction to have a denominator of 100. This directly gives us the percentage equivalent.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in many real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, and profit margins.
- Science: Expressing experimental results, statistical data, and concentrations.
- Business: Analyzing sales figures, market share, and growth rates.
- Everyday life: Calculating tips, understanding sale prices, and interpreting survey results.
Expanding on the Concept: Further Exploration of Fractions and Percentages
Let's consider some related concepts to deepen your understanding:
-
Decimal representation: The decimal equivalent of 30% is 0.30. This highlights the interrelationship between fractions, decimals, and percentages. They are simply different ways of representing the same proportion.
-
Percentage increase and decrease: Often, we need to calculate percentage changes. For example, if a quantity increases from 60 to 78, the percentage increase is calculated as: [(78-60)/60] x 100 = 30%. Similarly, a decrease can be calculated using the same formula.
-
Compounding percentages: In finance, compound interest involves applying a percentage increase to a growing value over time. Understanding compounding is essential for comprehending long-term financial growth.
-
Working with percentages greater than 100%: It's possible to have percentages exceeding 100%. This indicates a value more than the original amount. For instance, if something grows from 60 to 180, the percentage increase is [(180-60)/60] x 100 = 200%.
-
Percentages and proportions: Percentages are intrinsically linked to proportions. Understanding proportions is key to solving more complex percentage problems.
Frequently Asked Questions (FAQ)
-
Q: What if the fraction is an improper fraction (numerator > denominator)?
- A: The same principles apply. Divide the numerator by the denominator, and multiply the result by 100. The resulting percentage will be greater than 100%.
-
Q: How do I convert a percentage back to a fraction?
- A: Divide the percentage by 100, and simplify the resulting fraction. For example, 75% becomes 75/100, which simplifies to 3/4.
-
Q: Can I use a calculator for these conversions?
- A: Absolutely! Calculators significantly simplify the process, especially for more complex fractions.
-
Q: Are there any online tools to help with percentage calculations?
- A: Yes, many websites and apps offer percentage calculators. These can be very helpful for quick conversions and complex problems.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental skill with wide-ranging applications. The process is straightforward and can be approached using different methods, all based on the core principle of representing a proportion as a fraction of 100. By understanding the underlying principles and practicing different methods, you can confidently tackle percentage calculations in various contexts. Remember the key steps: divide the numerator by the denominator, and then multiply by 100. This simple yet powerful technique unlocks the ability to interpret and utilize percentages effectively in your daily life and professional endeavors. Practice makes perfect, so try converting different fractions to percentages to further reinforce your understanding. Remember to always check your work and consider using different methods to verify your answers. This will build your confidence and deepen your understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
Duties And Responsibility Of Manager
Sep 12, 2025
-
Lewis Dot Structure For Pcl5
Sep 12, 2025
-
Examples Of Contrast In Art
Sep 12, 2025
-
Periodic Table With Radioactive Elements
Sep 12, 2025
-
How Much Is A Million
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 18 60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.