19 35 As A Percentage
catronauts
Sep 14, 2025 · 5 min read
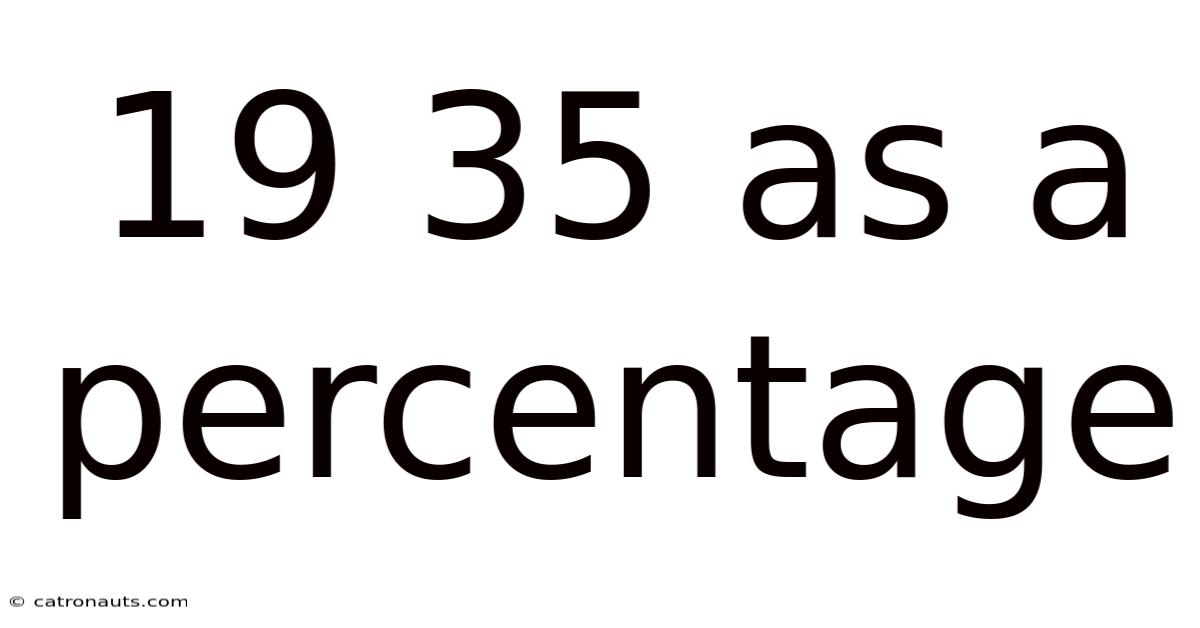
Table of Contents
19 out of 35: Understanding Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to advanced scientific calculations. This article delves into the process of calculating "19 out of 35 as a percentage," explaining the steps involved, providing context for various applications, and addressing frequently asked questions. Mastering this seemingly simple calculation unlocks a powerful tool for interpreting data and making informed decisions.
Understanding Percentages: A Foundation
A percentage represents a fraction of 100. The term "percent" literally means "per hundred." When we say "x percent," we mean x out of every 100. For example, 50% means 50 out of 100, which simplifies to one-half (1/2). This fundamental concept forms the basis for calculating any percentage.
Calculating 19 out of 35 as a Percentage: A Step-by-Step Guide
To calculate 19 out of 35 as a percentage, we follow these steps:
-
Establish the Fraction: The first step is to represent the given information as a fraction. "19 out of 35" translates directly to the fraction 19/35.
-
Convert the Fraction to a Decimal: To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number). In this case, we divide 19 by 35:
19 ÷ 35 ≈ 0.542857
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
0.542857 × 100 ≈ 54.29%
Therefore, 19 out of 35 is approximately 54.29%. Note that we've rounded the result to two decimal places for practicality.
Beyond the Calculation: Understanding the Context
While the calculation itself is straightforward, understanding the context in which this percentage might appear is crucial. Let's explore some examples:
-
Academic Performance: Imagine a student scoring 19 out of 35 on a test. A 54.29% score provides a clear indication of their performance relative to the total possible marks. This allows for easy comparison with other students and assessment of their understanding of the subject matter. The percentage provides a standardized measure, irrespective of the total number of marks.
-
Business Metrics: In business, percentages are frequently used to track performance indicators (KPIs). For example, if a company aimed to complete 35 projects and managed to finish 19, the 54.29% completion rate provides a quantifiable measure of their success. This data can be compared to previous periods or against competitor performance.
-
Survey Results: If a survey of 35 respondents revealed that 19 favored a particular option, the 54.29% represents the proportion of respondents holding that preference. This aggregated data simplifies understanding public opinion and can guide decision-making processes.
-
Scientific Data Analysis: In scientific research, percentages are often used to represent proportions within datasets. For example, if a researcher observed 19 successful trials out of 35, the resulting 54.29% success rate is a vital component in the analysis and interpretation of their experiment. This data is crucial for drawing conclusions and supporting or refuting hypotheses.
Different Methods of Calculation: Expanding Your Understanding
While the method outlined above is the most common approach, let's explore alternative ways to visualize and calculate this percentage. These methods offer deeper insight into the underlying mathematical principles:
-
Using Proportions: We can set up a proportion to solve this problem:
19/35 = x/100
To solve for x (the percentage), cross-multiply:
35x = 1900
x = 1900/35 ≈ 54.29
This method directly relates the fraction to the percentage representation.
-
Using a Calculator: Most calculators have a percentage function. Simply input 19 ÷ 35 and then multiply the resulting decimal by 100. This offers a quick and efficient way to arrive at the answer.
-
Mental Estimation: For a quick, rough estimate, you can round the numbers. For example, thinking of 20/35 which simplifies approximately to 4/7, allows for a mental estimation, especially useful in situations where precise accuracy isn't critical.
Addressing Common Questions and Misconceptions
Understanding percentages often involves navigating common questions and misconceptions. Let's address some of them:
-
Rounding: Rounding percentages depends on the level of precision required. For general purposes, rounding to two decimal places (54.29%) is often sufficient. However, in scientific applications or financial contexts, more precise rounding might be necessary.
-
Significant Figures: The number of significant figures in the result should align with the significant figures in the original numbers. Since 19 and 35 both have two significant figures, rounding the result to two significant figures is appropriate.
-
Percentage Increase/Decrease: This calculation only shows the proportion of 19 out of 35. To calculate a percentage increase or decrease you would need a comparison point (e.g., a previous value). For example, if there were 25 successful trials previously, then an increase of (19-25)/25 * 100% would reveal a percentage decrease.
-
Percentage Points: It's important to distinguish between percentage points and percentages. A change from 20% to 50% is a 30 percentage point increase, not a 150% increase.
Expanding Applications and Real-World Scenarios
The ability to calculate percentages extends far beyond simple academic exercises. Here are some real-world scenarios where understanding percentages proves crucial:
-
Financial Literacy: Calculating interest rates, discounts, tax rates, and profit margins all rely on a solid grasp of percentages. This knowledge empowers individuals to make informed financial decisions.
-
Data Interpretation: From analyzing survey results to understanding economic indicators, the ability to interpret and utilize percentages is vital in comprehending data effectively.
-
Scientific Research: Percentages are fundamental in scientific analyses, particularly in expressing probabilities, statistical significance, and experimental results.
-
Everyday Life: Calculating tips, comparing prices, understanding sales, and even cooking recipes can benefit from a solid understanding of percentages.
Conclusion: Mastering the Power of Percentages
Calculating 19 out of 35 as a percentage, which equates to approximately 54.29%, is more than just a mathematical exercise. It is a gateway to understanding and interpreting data across numerous disciplines. By mastering this seemingly simple calculation, you equip yourself with a powerful tool for making informed decisions, analyzing data effectively, and navigating the complexities of the world around you. This fundamental understanding empowers you to interpret data critically, analyze information accurately, and apply this knowledge in various aspects of your personal and professional life. The more comfortable you become with percentage calculations, the more confident you will be in tackling complex problems and interpreting information effectively.
Latest Posts
Latest Posts
-
Difference Between Tangible And Intangible
Sep 15, 2025
-
Rightward Shift In Demand Curve
Sep 15, 2025
-
Catholic Adam And Eve Story
Sep 15, 2025
-
What Is Anionic And Cationic
Sep 15, 2025
-
Legal Consent Age In Mississippi
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 19 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.