2 5 Divided By 2
catronauts
Sep 13, 2025 · 7 min read
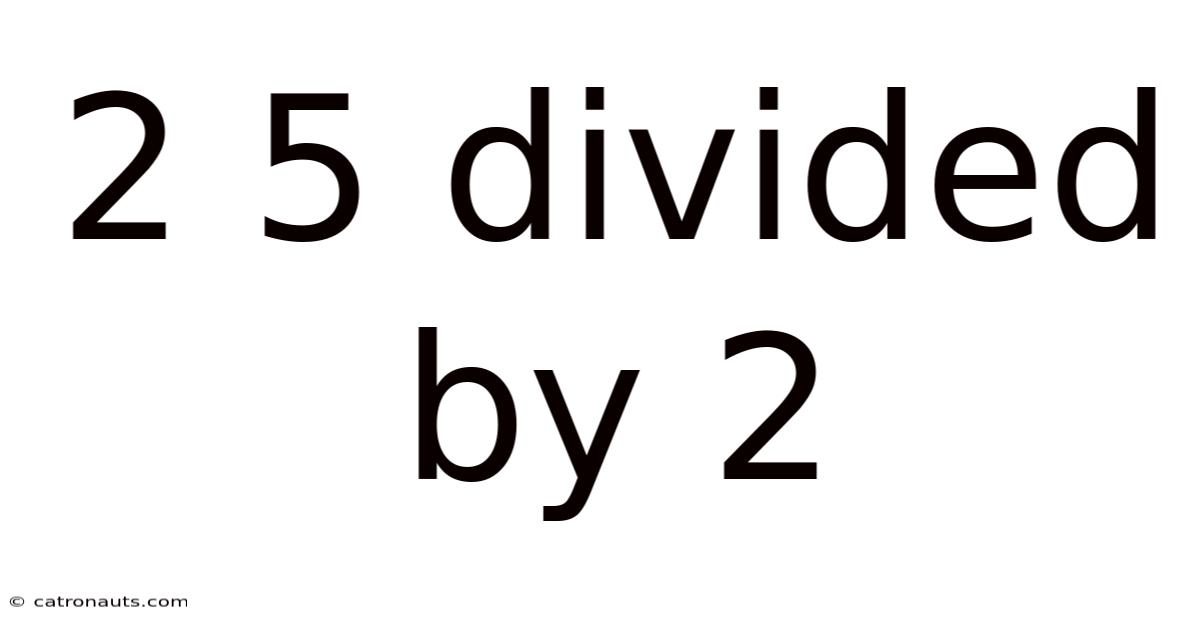
Table of Contents
Unpacking the Mystery: 25 Divided by 2
Understanding division is a cornerstone of mathematics, forming the basis for countless applications in everyday life, from splitting bills fairly to calculating unit prices. This article delves into the seemingly simple problem of 25 divided by 2, exploring various methods of solving it and uncovering the deeper mathematical principles at play. We'll go beyond a simple numerical answer, exploring different interpretations of division and the valuable lessons it teaches about fractions, decimals, and real-world applications.
Introduction: More Than Just a Calculation
The seemingly straightforward question, "What is 25 divided by 2?", opens a door to a wealth of mathematical concepts. While the immediate answer might seem obvious to some, a complete understanding requires exploring different approaches and interpretations. This article aims to provide a comprehensive analysis, suitable for learners of all levels, from those just beginning to grasp division to those seeking a more nuanced understanding of its applications. We will examine the process, its results in different forms (whole numbers, fractions, decimals), and the implications for problem-solving in various contexts.
Method 1: Long Division – A Classic Approach
The most traditional method of solving 25 divided by 2 is through long division. This method provides a step-by-step process that clearly demonstrates the division process:
-
Set up the problem: Write 25 as the dividend (the number being divided) and 2 as the divisor (the number doing the dividing).
-
Divide the tens digit: How many times does 2 go into 2 (the tens digit of 25)? The answer is 1. Write 1 above the 2 in 25.
-
Multiply and subtract: Multiply the quotient (1) by the divisor (2), resulting in 2. Subtract this from the tens digit of the dividend (2 - 2 = 0).
-
Bring down the ones digit: Bring down the ones digit of the dividend (5).
-
Divide the remainder: How many times does 2 go into 5? The answer is 2 with a remainder of 1. Write 2 next to the 1 in the quotient.
-
Final result: The quotient is 12 with a remainder of 1. This can be written as 12 R 1.
Method 2: Fractions – Representing the Remainder
The remainder in long division often presents a more refined perspective. Instead of simply expressing the result as 12 R 1, we can represent it as a fraction. The remainder (1) becomes the numerator, and the divisor (2) becomes the denominator. Therefore, 25 divided by 2 equals 12 ½. This fractional representation provides a more precise answer, eliminating ambiguity. This form highlights the concept of improper fractions, where the numerator is larger than the denominator. This can also be expressed as a mixed number, combining a whole number (12) and a fraction (½).
Method 3: Decimals – A More Precise Answer
While fractions accurately represent the remainder, decimals offer another level of precision. To convert the remainder to a decimal, continue the long division process. Add a decimal point and a zero to the remainder (1).
-
Divide the remainder: 2 goes into 10 five times.
-
Result: The result is 12.5. This decimal representation offers an even more precise answer than the fractional form and is widely used in various applications.
Understanding the Concepts: Division, Quotients, and Remainders
The process of division involves splitting a quantity into equal parts. The dividend is the total quantity being divided, the divisor is the number of equal parts, and the quotient is the result of the division. When the division doesn't result in a whole number, a remainder is left. This remainder represents the portion of the dividend that wasn't fully divided by the divisor.
Understanding the relationship between the dividend, divisor, quotient, and remainder is crucial. They are interconnected and represent different aspects of the division process. The ability to interpret and utilize these components allows for accurate calculations and a deeper comprehension of mathematical principles.
Real-World Applications: Beyond the Textbook
The simple problem of 25 divided by 2 extends far beyond theoretical mathematics. Consider these scenarios:
-
Sharing resources: If you have 25 candies and want to share them equally between two friends, each friend receives 12 candies, and you have 1 candy left over. The fraction (1/2) or decimal (0.5) represents the half candy that remains.
-
Calculating unit prices: If a 25-meter roll of fabric costs $50, dividing the total cost by the length gives you the price per meter ($2.50).
-
Averaging data: If you need to calculate the average of two scores (e.g., 20 and 30), adding them and then dividing by 2 provides the average score (25).
-
Measurement conversions: Converting units frequently involves division. For instance, converting inches to feet necessitates dividing the number of inches by 12 (inches per foot).
These examples demonstrate the practical relevance of division and its ability to solve real-world problems across various fields.
Exploring Deeper Mathematical Concepts: Fractions and Decimals
This problem serves as an excellent opportunity to reinforce our understanding of fractions and decimals. The fractional representation (12 ½) emphasizes the concept of parts of a whole, while the decimal representation (12.5) highlights the use of tenths, hundredths, and beyond to express values precisely. Both representations are vital in various mathematical applications and real-world contexts.
The ability to seamlessly convert between fractions and decimals is a significant skill in mathematics. This interoperability allows for flexibility in representing and solving problems, choosing the most convenient format depending on the context and the required precision.
Addressing Common Misconceptions
A common misconception surrounding division is the incorrect handling of remainders. Some students might simply disregard the remainder, leading to inaccurate results. However, understanding the significance of the remainder—whether represented as a fraction or a decimal—is essential for achieving precise and meaningful answers. It's important to emphasize the concept of the remainder as a part of the whole, not something to be ignored.
Another misconception relates to the order of operations. When performing a series of calculations, it is crucial to follow the established order of operations (PEMDAS/BODMAS), ensuring that division is performed correctly relative to other mathematical operations. Failing to follow this order can lead to inaccurate results.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to solve 25 divided by 2? A: Yes, calculators efficiently provide the answer (12.5). However, it's crucial to understand the underlying mathematical principles and methods involved.
-
Q: Why are there multiple ways to represent the answer (12 R 1, 12 ½, 12.5)? A: Different representations offer varying degrees of precision and context. The remainder, fraction, and decimal representations each serve a unique purpose.
-
Q: Which representation is "better," fraction or decimal? A: Neither representation is inherently "better." The optimal choice depends on the specific context and the desired level of precision. Fractions are often preferred when dealing with exact quantities, whereas decimals are commonly used in applications requiring greater precision.
Conclusion: A Foundation for Further Learning
The seemingly simple problem of 25 divided by 2 offers a rich learning experience, encompassing fundamental mathematical concepts and extending into practical applications. Beyond the numerical answer, this problem provides a platform to strengthen our understanding of division, fractions, decimals, remainders, and their relevance in various real-world scenarios. Mastering these concepts builds a strong foundation for more advanced mathematical studies and problem-solving abilities. By understanding not just the "how" but also the "why" behind each step, we transform a basic arithmetic problem into a gateway to a more profound understanding of mathematics and its applications in our daily lives. The journey of understanding 25 divided by 2 is not just about finding the answer; it's about developing a deeper appreciation for the beauty and practicality of mathematical principles.
Latest Posts
Latest Posts
-
Was Robin Of Locksley Real
Sep 13, 2025
-
How Many Ounces In 600ml
Sep 13, 2025
-
Has The Quran Been Altered
Sep 13, 2025
-
How Do You Find Deceleration
Sep 13, 2025
-
105 Degrees F To C
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 5 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.