20 27 As A Percentage
catronauts
Sep 13, 2025 · 5 min read
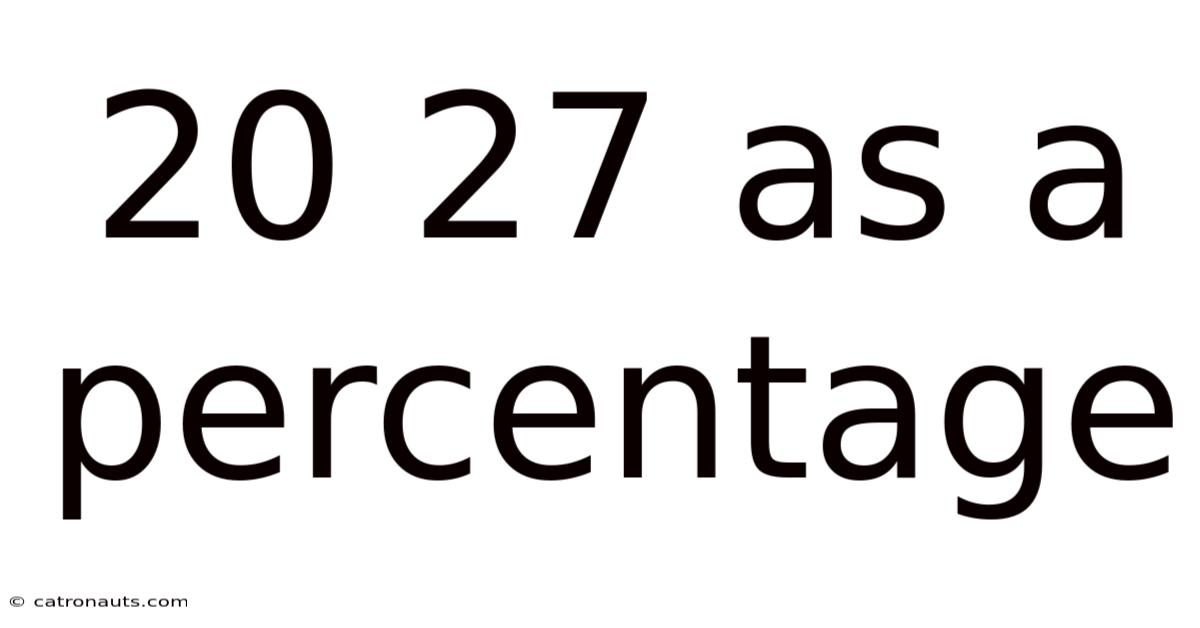
Table of Contents
20 of 27 as a Percentage: A Comprehensive Guide
Finding the percentage one number represents of another is a fundamental skill in mathematics with applications spanning numerous fields, from calculating grades and discounts to understanding financial reports and statistical data. This comprehensive guide will walk you through how to calculate "20 of 27 as a percentage," explaining the process step-by-step, exploring different methods, and delving into the underlying mathematical principles. We'll also cover common applications and address frequently asked questions. By the end, you'll not only know the answer but also understand the broader concept of percentage calculations.
Understanding Percentages
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using the Formula
The most straightforward method to calculate "20 of 27 as a percentage" involves using a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 20 (the number we're interested in expressing as a percentage)
- Whole: 27 (the total number)
Substituting these values into the formula:
(20 / 27) * 100% = ≈ 74.07%
Therefore, 20 represents approximately 74.07% of 27.
Method 2: Converting to Decimal and Multiplying
An alternative approach involves first converting the fraction 20/27 into a decimal and then multiplying by 100%. To convert a fraction to a decimal, we divide the numerator (top number) by the denominator (bottom number):
20 ÷ 27 ≈ 0.7407
Now, multiply the decimal by 100%:
0.7407 * 100% = 74.07%
This method yields the same result as the formula method.
Method 3: Using Proportions
Percentage problems can also be solved using proportions. We can set up a proportion:
20/27 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
20 * 100 = 27 * x
2000 = 27x
x = 2000 / 27 ≈ 74.07
Again, this method confirms our previous result.
Understanding the Result: 74.07%
The result, approximately 74.07%, means that 20 is approximately 74.07 out of every 100 parts of 27. This is a crucial piece of information in various contexts. For instance, if 27 represents the total number of students in a class and 20 students passed an exam, then the pass rate is approximately 74.07%.
Rounding and Precision
In practical applications, you might need to round the percentage to a certain number of decimal places or to the nearest whole number. The level of precision needed depends on the context. For instance, in a casual conversation, rounding to 74% might suffice. However, in a scientific report or financial statement, greater precision might be required.
Practical Applications of Percentage Calculations
The ability to calculate percentages is indispensable in numerous real-world situations. Here are some examples:
- Calculating Grades: If you scored 20 points out of a possible 27 points on a test, your score is approximately 74.07%.
- Determining Discounts: A store offers a 20% discount on an item priced at $27. The discount amount is (20/100) * $27 = $5.40, and the final price is $27 - $5.40 = $21.60.
- Analyzing Financial Statements: Percentage changes in revenue, expenses, or profits are crucial for understanding a company's financial performance.
- Understanding Statistical Data: Percentages are frequently used to represent proportions in surveys, polls, and other statistical analyses. For instance, if 20 out of 27 respondents prefer a particular product, the preference rate is approximately 74.07%.
- Calculating Taxes: Tax rates are expressed as percentages, allowing for easy calculation of tax amounts.
- Working with Ratios and Proportions: Percentage calculations are inherently linked to ratios and proportions, making them vital for solving problems in various fields.
Advanced Percentage Calculations: Beyond the Basics
While calculating "20 of 27 as a percentage" is a fundamental exercise, let's explore some related concepts:
- Finding the Percentage Increase or Decrease: Suppose a value increases from 20 to 27. The percentage increase is calculated as: [(27 - 20) / 20] * 100% = 35%. Conversely, if a value decreases from 27 to 20, the percentage decrease is: [(27 - 20) / 27] * 100% ≈ 25.93%.
- Calculating Percentage Points: Percentage points represent the absolute difference between two percentages. For instance, if the interest rate increases from 5% to 8%, the increase is 3 percentage points, not 3%.
- Working with Compound Percentages: Compound percentages involve applying a percentage change repeatedly over time. Understanding compound interest is a crucial skill in finance.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage with a larger or smaller number?
A: The method remains the same. Simply substitute the new values into the formula: (Part / Whole) * 100%.
Q: Is there a way to do this calculation without a calculator?
A: For simpler fractions, mental math or long division might be possible. However, for more complex fractions, a calculator is usually more efficient and accurate.
Q: What if the "whole" number is zero?
A: Dividing by zero is undefined in mathematics. You cannot calculate a percentage when the whole number is zero.
Q: Can I use a spreadsheet program like Excel or Google Sheets to calculate percentages?
A: Yes, spreadsheets provide built-in functions for calculating percentages, simplifying the process significantly.
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare proportions and express relative amounts, making them crucial for understanding and interpreting data in many fields.
Conclusion
Calculating "20 of 27 as a percentage" involves a straightforward process, yet it represents a foundational concept with wide-ranging applications. Mastering percentage calculations equips you with a vital skill for tackling problems in various contexts, from everyday life to professional settings. Remember the formula (Part / Whole) * 100% and choose the method that best suits your needs and the complexity of the problem. By understanding the underlying principles and practicing different approaches, you'll become proficient in calculating percentages and interpreting the results effectively. This understanding will undoubtedly enhance your problem-solving skills and data analysis capabilities.
Latest Posts
Latest Posts
-
Rude Words Starting With M
Sep 13, 2025
-
Shri Guru Nanak Dev Ji
Sep 13, 2025
-
My Name Is In Germany
Sep 13, 2025
-
Formal Assessment And Informal Assessment
Sep 13, 2025
-
Convert 42 C To F
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 20 27 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.