20 35 As A Percent
catronauts
Sep 12, 2025 · 5 min read
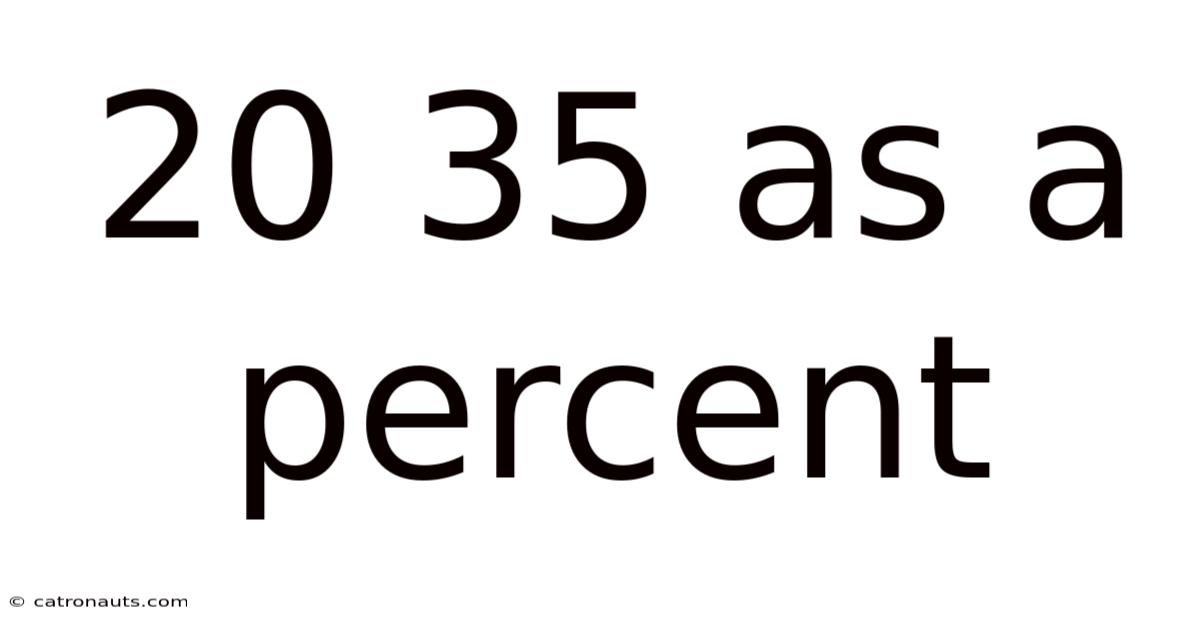
Table of Contents
Decoding 20 out of 35: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various fields, from academic studies to everyday financial transactions. This article will delve deep into calculating the percentage represented by 20 out of 35, exploring the process step-by-step, providing alternative methods, and addressing common questions surrounding percentage calculations. We'll also examine the practical applications of this specific calculation and discuss related concepts to solidify your understanding. By the end, you'll not only know the answer but also possess a robust understanding of percentage calculations.
Understanding Percentages: The Basics
Before jumping into the calculation of 20 out of 35 as a percentage, let's establish a solid foundation. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to ½ or 0.5 as a decimal.
Percentages are useful for comparing different quantities, expressing proportions, and showing changes or growth rates. They provide a standardized way to understand ratios, making them easily comparable and interpretable regardless of the original quantities involved.
Calculating 20 out of 35 as a Percentage: The Step-by-Step Approach
The most straightforward method to calculate the percentage involves three simple steps:
Step 1: Formulate the Fraction
First, express the given numbers as a fraction. In this case, we have 20 out of 35, which can be written as 20/35.
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
20 ÷ 35 = 0.57142857...
Step 3: Convert the Decimal to a Percentage
Finally, multiply the decimal by 100 to express it as a percentage:
0.57142857... × 100 = 57.142857...%
Therefore, 20 out of 35 is approximately 57.14%. The "..." indicates that the decimal continues infinitely; however, for most practical purposes, rounding to two decimal places (57.14%) is sufficient.
Alternative Methods for Percentage Calculation
While the above method is the most common, there are alternative approaches that can be used, especially when dealing with more complex scenarios:
- Using Proportions: You can set up a proportion to solve for the percentage. Let 'x' represent the percentage:
20/35 = x/100
Cross-multiplying gives:
35x = 2000
Solving for x:
x = 2000/35 ≈ 57.14%
-
Using a Calculator: Most calculators have a percentage function that simplifies the calculation. Simply enter 20 ÷ 35 and then multiply by 100 to obtain the percentage directly.
-
Simplifying the Fraction: Before converting to a decimal, you can simplify the fraction 20/35 by finding the greatest common divisor (GCD) of both numbers. The GCD of 20 and 35 is 5. Dividing both the numerator and denominator by 5 simplifies the fraction to 4/7. Then convert 4/7 to a decimal and multiply by 100 to get the percentage. This method helps in handling larger numbers more efficiently.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world situations:
-
Academic Performance: Calculating grades and assessing academic progress frequently involves percentage calculations. For example, if a student answers 20 questions correctly out of 35, their score is 57.14%.
-
Financial Matters: Percentages are crucial in understanding interest rates, discounts, taxes, and investment returns. Calculating the percentage increase or decrease in savings or expenses is a common application.
-
Data Analysis: Percentages are commonly used to represent proportions and trends in data analysis and research. They facilitate the comparison of different data sets and the visualization of statistical findings.
-
Retail and Sales: Discounts are often expressed as percentages (e.g., "20% off"). Calculating the final price after a discount requires percentage calculations.
-
Everyday Life: Percentage calculations are used to calculate tips, estimate proportions in recipes, and understand various statistical information presented in the news or other media.
Addressing Frequently Asked Questions (FAQ)
Here are some frequently asked questions related to percentage calculations:
Q1: What if I have a number larger than 100%?
A1: A percentage greater than 100% simply means that the quantity being considered is greater than the reference value. For example, if sales this year are 120% of last year's sales, it means that sales have increased by 20% compared to the previous year.
Q2: How do I calculate a percentage increase or decrease?
A2: To calculate a percentage increase, find the difference between the new and original values, divide the difference by the original value, and then multiply by 100. For a percentage decrease, the process is similar, but the difference is negative.
Q3: How do I convert a percentage back to a fraction or decimal?
A3: To convert a percentage to a decimal, divide by 100. To convert a percentage to a fraction, express the percentage as a fraction with a denominator of 100, and then simplify the fraction if possible.
Q4: What is the difference between percentage and proportion?
A4: While closely related, percentage and proportion represent different but connected concepts. A proportion is a relationship between two quantities, while a percentage is a specific type of proportion expressed as a value out of 100. The percentage is a way of expressing a proportion in a standardized and easy-to-understand format.
Conclusion: Mastering Percentage Calculations
Calculating 20 out of 35 as a percentage, which results in approximately 57.14%, is a straightforward process. Understanding the underlying principles of percentage calculations is crucial for various aspects of life, from academic pursuits to financial planning. This article provided a detailed explanation of different methods, highlighted practical applications, and addressed common questions to enhance your understanding. By mastering percentage calculations, you equip yourself with a valuable skill applicable in numerous contexts and contribute to more confident and informed decision-making. Remember to practice regularly to solidify your understanding and improve your calculation speed and accuracy. Don't hesitate to review the steps and alternative methods described above to build a strong foundation in this essential mathematical concept.
Latest Posts
Latest Posts
-
Convert 24 Oz To Grams
Sep 12, 2025
-
Differences Between Refraction And Reflection
Sep 12, 2025
-
Model Of Human Body Organs
Sep 12, 2025
-
Alfred Lord Tennyson In Memoriam
Sep 12, 2025
-
Oldest Mountain Range In World
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 20 35 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.