21 40 As A Percent
catronauts
Sep 18, 2025 · 6 min read
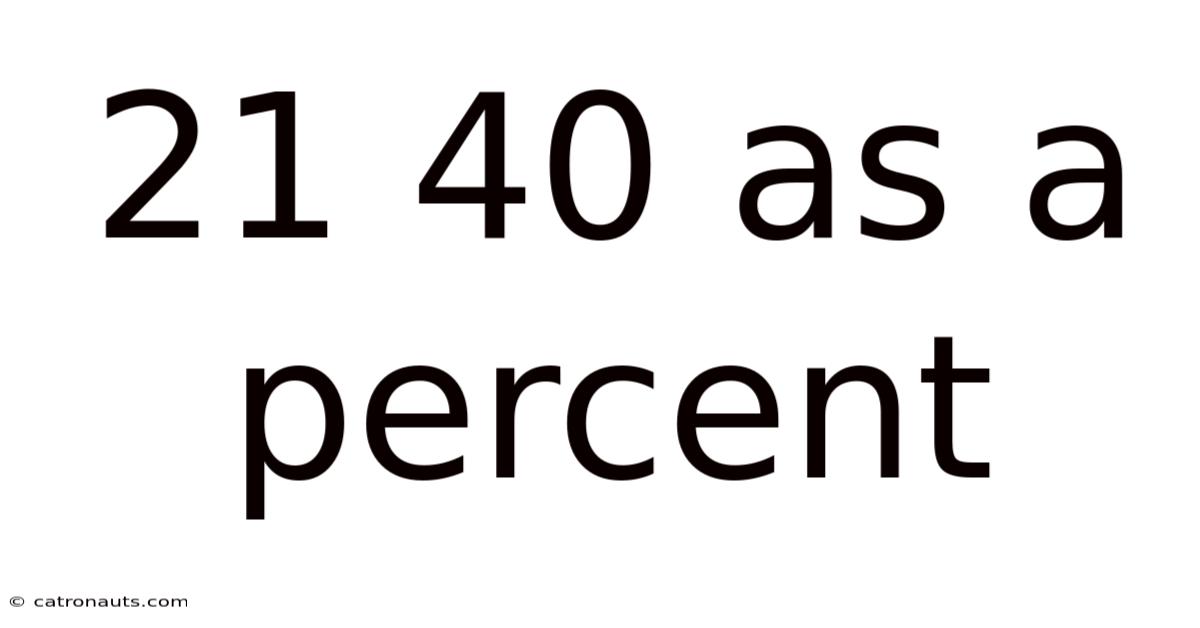
Table of Contents
21/40 as a Percent: A Comprehensive Guide to Percentage Conversions
Understanding percentages is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts and taxes to understanding statistics and financial reports. This article will provide a comprehensive guide on how to convert the fraction 21/40 into a percentage, exploring different methods and delving into the underlying concepts. We'll also address common misconceptions and provide further examples to solidify your understanding. By the end, you'll be confident in converting fractions to percentages and applying this knowledge to various real-world scenarios.
Introduction: Understanding Fractions and Percentages
Before diving into the conversion of 21/40 to a percentage, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For instance, in the fraction 21/40, 21 represents the part and 40 represents the whole.
A percentage, denoted by the symbol %, represents a fraction of 100. It essentially expresses a fraction as a part of 100. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2. Percentages provide a standardized way to compare proportions and are widely used in various fields.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most straightforward method for converting 21/40 into a percentage. It involves two simple steps:
-
Convert the fraction to a decimal: To do this, divide the numerator (21) by the denominator (40).
21 ÷ 40 = 0.525
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%).
0.525 × 100 = 52.5%
Therefore, 21/40 is equal to 52.5%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. Since percentages are based on 100, this directly gives us the percentage.
To find an equivalent fraction with a denominator of 100, we need to determine what number we must multiply 40 by to get 100. This is simply 100 ÷ 40 = 2.5.
Now, we multiply both the numerator and the denominator of 21/40 by 2.5:
(21 × 2.5) / (40 × 2.5) = 52.5 / 100
This means that 21/40 is equivalent to 52.5/100, which is equal to 52.5%.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage. We can set up a proportion:
21/40 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
40x = 2100
Now, divide both sides by 40:
x = 2100 ÷ 40 = 52.5
Therefore, x = 52.5%, confirming our previous results. This method emphasizes the relationship between the fraction and the percentage, illustrating the core concept behind percentage calculations.
A Deeper Dive into Percentage Calculations: Understanding the Concept of Ratio
The conversion of fractions to percentages fundamentally relies on the concept of ratio. A ratio compares two quantities, showing their relative sizes. In the fraction 21/40, the ratio is 21:40. Converting this ratio to a percentage means expressing this relationship as a part of 100.
Think of it this way: if you have 21 successful outcomes out of 40 total attempts, what percentage of your attempts were successful? The percentage represents the proportion of successful outcomes relative to the total number of attempts. This is why understanding ratios is crucial to grasping the concept of percentages.
Practical Applications: Real-World Examples
Understanding percentage calculations is essential for various everyday tasks. Here are a few examples:
- Discounts: If a store offers a 20% discount on an item, and the original price is $100, you can calculate the discount amount and the final price using percentage calculations.
- Taxes: Calculating sales tax or income tax involves applying a percentage to the base amount.
- Grade Calculations: Many educational systems use percentages to represent grades and scores. Converting raw scores to percentages allows for a standardized comparison of performance.
- Financial Analysis: Percentages are heavily used in financial reports and analysis, including profit margins, interest rates, and investment returns.
- Data Analysis and Statistics: Percentages are vital for interpreting and presenting data in a concise and easily understandable manner. They help in visualizing proportions and trends.
Common Mistakes to Avoid
While converting fractions to percentages is relatively straightforward, some common mistakes can lead to incorrect results. These include:
- Incorrect order of operations: When converting a fraction to a decimal, ensure you divide the numerator by the denominator, not the other way around.
- Forgetting to multiply by 100: Remember to multiply the decimal by 100 to obtain the percentage.
- Misinterpreting decimal places: Pay attention to the decimal places when working with decimals and percentages. A misplaced decimal point can significantly affect the result.
- Confusing percentage with decimal value: Remember that a decimal is not the same as a percentage. A decimal represents a portion of one, whereas a percentage represents that portion as a fraction of 100.
Frequently Asked Questions (FAQ)
-
Q: Can I convert any fraction to a percentage? A: Yes, any fraction can be converted to a percentage using the methods described above.
-
Q: What if the resulting percentage is a decimal? A: It's perfectly acceptable to have a decimal in a percentage. For example, 52.5% is a perfectly valid percentage.
-
Q: How can I convert a percentage back to a fraction? A: To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 52.5% = 52.5/100 = 105/200 = 21/40.
-
Q: Are there any online calculators for percentage conversions? A: Yes, many online calculators are available for converting fractions and decimals to percentages and vice versa. These can be helpful for checking your work or for quick calculations. However, understanding the underlying principles remains essential.
Conclusion: Mastering Percentage Conversions
Converting 21/40 to a percentage, which equals 52.5%, demonstrates a fundamental skill in mathematics with numerous real-world applications. By understanding the different methods—converting to a decimal, finding an equivalent fraction with a denominator of 100, and using proportions—you've gained a solid foundation in percentage calculations. Remember to practice regularly, avoid common mistakes, and apply this knowledge to diverse scenarios to build your proficiency. With practice and a clear understanding of the underlying concepts, you can confidently tackle percentage problems in any context. The ability to convert fractions to percentages isn't just a mathematical skill; it's a valuable tool for navigating the numerical aspects of everyday life.
Latest Posts
Latest Posts
-
Describing Words Beginning With L
Sep 18, 2025
-
Passive Sentences In Simple Present
Sep 18, 2025
-
Equivalent Fractions To 3 12
Sep 18, 2025
-
Data Types Sizes In Java
Sep 18, 2025
-
What Is Importer And Exporter
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 21 40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.