25 10 As A Decimal
catronauts
Sep 10, 2025 · 6 min read
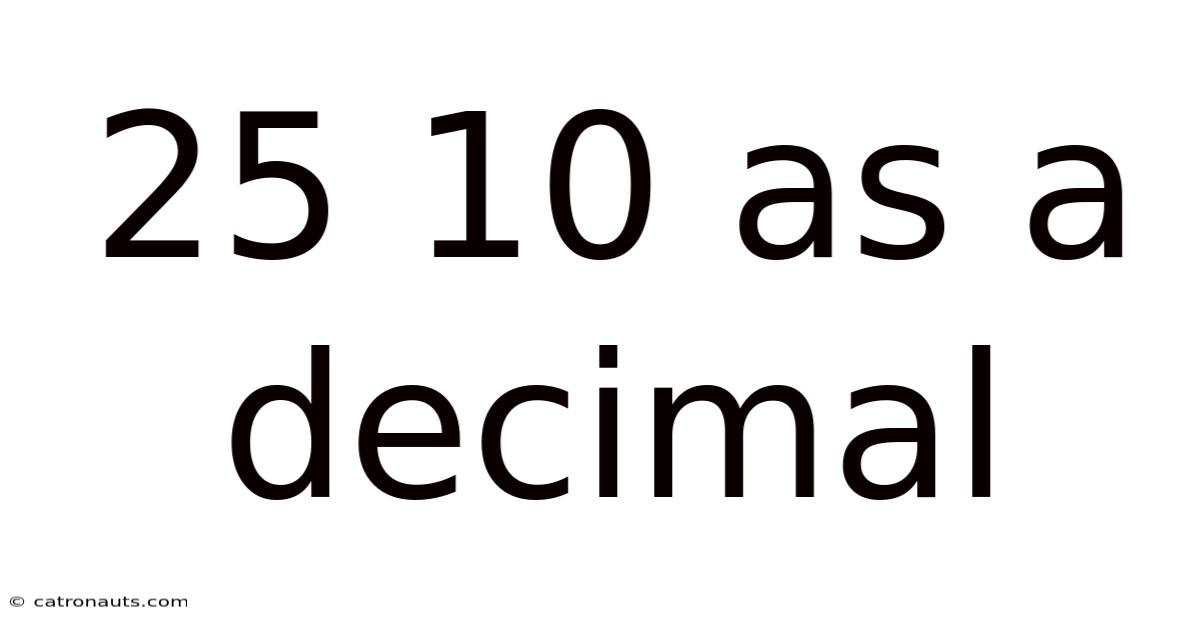
Table of Contents
Understanding 25/10 as a Decimal: A Comprehensive Guide
Fractions and decimals are fundamental concepts in mathematics, representing parts of a whole. Converting fractions to decimals is a crucial skill applicable across numerous fields, from everyday calculations to advanced scientific applications. This article delves deep into understanding the conversion of the fraction 25/10 into its decimal equivalent, explaining the process, its applications, and addressing common related queries. We'll explore the underlying principles, providing a clear and comprehensive guide suitable for learners of all levels. This exploration will also cover related concepts like percentage conversion and different methods for tackling similar fractional conversions. By the end, you'll not only know the decimal equivalent of 25/10 but also possess a solid understanding of the broader mathematical principles involved.
Introduction to Fractions and Decimals
Before jumping into the conversion of 25/10, let's briefly review the basics of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, in the fraction 25/10, 25 is the numerator and 10 is the denominator. This signifies 25 parts out of a total of 10 parts.
A decimal is another way of representing a part of a whole, using a base-10 system. It uses a decimal point (.) to separate the whole number part from the fractional part. For instance, 2.5 is a decimal, where '2' represents the whole number and '.5' represents the fractional part (five-tenths).
The key relationship between fractions and decimals is that they are interchangeable. Any fraction can be expressed as a decimal, and vice-versa. This conversion is often necessary for easier calculations or to represent data in a more accessible format.
Converting 25/10 to a Decimal: The Simple Method
The simplest way to convert 25/10 to a decimal is through direct division. We divide the numerator (25) by the denominator (10):
25 ÷ 10 = 2.5
Therefore, the decimal equivalent of 25/10 is 2.5. This is a straightforward process because the denominator (10) is a power of 10 (10¹). Converting fractions with denominators that are powers of 10 is particularly easy.
Converting 25/10 to a Decimal: Understanding the Process
The division process reveals the underlying principle. The fraction 25/10 means "25 divided by 10". When we perform this division, we're essentially finding out how many times 10 goes into 25. It goes in twice (2 x 10 = 20), leaving a remainder of 5. This remainder is expressed as a fraction of the divisor (10), resulting in 5/10, which simplifies to 0.5. Combining the whole number part (2) and the fractional part (0.5) gives us the decimal 2.5.
Alternative Methods for Converting Fractions to Decimals
While direct division is the most straightforward method for 25/10, let's explore alternative approaches that are useful for more complex fractions:
- Simplifying the Fraction: Before converting, simplifying the fraction can make the division easier. In this case, 25/10 can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 5:
25 ÷ 5 = 5 10 ÷ 5 = 2
This simplifies the fraction to 5/2. Now, dividing 5 by 2 gives us 2.5, the same decimal equivalent.
- Converting to an Equivalent Fraction with a Denominator of 100 (or 1000, etc.): This method is particularly useful when dealing with fractions that don't have denominators that are powers of 10. For instance, if we had a fraction like 3/4, we could convert it to an equivalent fraction with a denominator of 100:
3/4 = (3 x 25) / (4 x 25) = 75/100
Since 75/100 represents 75 hundredths, this directly translates to the decimal 0.75.
- Using a Calculator: Calculators provide a quick and efficient way to convert fractions to decimals. Simply enter the fraction (25/10) and press the equals button to obtain the decimal equivalent.
Applications of Decimal Conversion
The ability to convert fractions to decimals is vital in various contexts:
-
Financial Calculations: Working with percentages, interest rates, and currency conversions frequently involves decimal representation.
-
Scientific Measurements: Many scientific measurements are expressed using decimals for greater precision.
-
Engineering and Construction: Precise measurements and calculations in these fields rely heavily on decimal numbers.
-
Data Analysis: Presenting and interpreting data often involves converting fractions into decimals for clarity and ease of comparison.
-
Everyday Calculations: From calculating tips at a restaurant to determining discounts in sales, decimal conversions are frequently utilized in our daily lives.
Percentage Conversion from 25/10
A closely related concept is percentage conversion. A percentage represents a fraction out of 100. To convert 25/10 to a percentage:
- Convert the fraction to a decimal: 25/10 = 2.5
- Multiply the decimal by 100: 2.5 x 100 = 250
- Add the percentage sign: 250%
Therefore, 25/10 is equivalent to 250%. This signifies that 25/10 represents 250 parts out of 100 parts, or 2 and a half times the whole.
Frequently Asked Questions (FAQ)
- Q: Why is it important to understand fraction-to-decimal conversion?
A: It's essential for performing various calculations, understanding data, and applying mathematical concepts across different fields, from finance to science. It allows for flexibility in representing numerical information.
- Q: What if the fraction has a denominator that is not a power of 10?
A: You can either simplify the fraction first, convert it to an equivalent fraction with a power-of-10 denominator, or use long division or a calculator to find the decimal equivalent.
- Q: Can all fractions be expressed as terminating decimals?
A: No. Fractions with denominators that contain prime factors other than 2 and 5 will result in non-terminating, repeating decimals (e.g., 1/3 = 0.333...).
- Q: What is the difference between a terminating and a repeating decimal?
A: A terminating decimal has a finite number of digits after the decimal point (e.g., 0.75). A repeating decimal has a digit or a group of digits that repeat infinitely (e.g., 0.333...).
- Q: How can I practice converting fractions to decimals?
A: Practice with various fractions, starting with simple ones and gradually increasing complexity. You can use online resources, worksheets, or textbooks to find practice problems.
Conclusion
Converting fractions to decimals is a fundamental skill with wide-ranging applications. The conversion of 25/10 to its decimal equivalent, 2.5, is a straightforward process, readily achieved through direct division. Understanding the underlying principles, exploring alternative methods, and recognizing the relationship between fractions, decimals, and percentages enhances mathematical proficiency. By mastering this crucial skill, you'll be better equipped to tackle more complex mathematical challenges and excel in numerous academic and professional endeavors. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities. This detailed explanation should provide a strong foundation for anyone seeking to grasp the nuances of fraction-to-decimal conversion.
Latest Posts
Latest Posts
-
Civil Law Cases In Australia
Sep 10, 2025
-
Book The View From Saturday
Sep 10, 2025
-
Old Black And White Movies
Sep 10, 2025
-
Inputs And Outputs Of Photosynthesis
Sep 10, 2025
-
Seven Hours Ago From Now
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 25 10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.