25 80 As A Percent
catronauts
Sep 12, 2025 · 5 min read
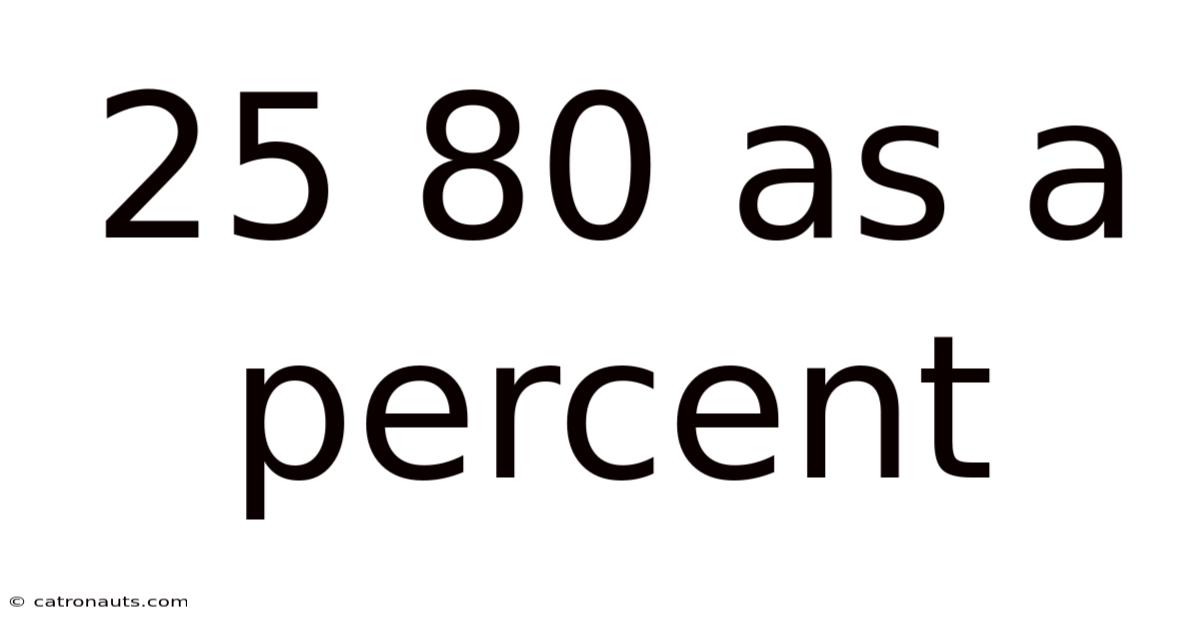
Table of Contents
25/80 as a Percent: A Comprehensive Guide to Understanding Percentage Calculations
Understanding percentages is a fundamental skill applicable in numerous everyday situations, from calculating discounts and sales tax to interpreting statistical data and assessing financial performance. This article provides a comprehensive guide to converting fractions to percentages, focusing specifically on expressing 25/80 as a percentage. We'll explore various methods, delve into the underlying mathematical principles, and address common questions surrounding percentage calculations. This guide is designed to be accessible to learners of all levels, building confidence and competence in this essential mathematical concept.
Understanding Fractions and Percentages
Before diving into the specific calculation of 25/80 as a percentage, let's review the basics. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 25/80, 25 is the numerator and 80 is the denominator. This means we're considering 25 parts out of a total of 80 parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It indicates how many parts per hundred make up the whole. For instance, 50% signifies 50 parts out of 100, which is equivalent to the fraction 50/100 or 1/2.
Method 1: Converting the Fraction Directly
The most straightforward method to express 25/80 as a percentage involves converting the fraction into an equivalent fraction with a denominator of 100. However, in this case, 80 doesn't divide evenly into 100. Therefore, we'll need to use a slightly different approach. We can simplify the fraction first:
Both 25 and 80 are divisible by 5. Simplifying the fraction, we get:
25 ÷ 5 = 5 80 ÷ 5 = 16
So, 25/80 simplifies to 5/16. Now, to convert this simplified fraction to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by dividing 100 by the denominator (16):
100 ÷ 16 = 6.25
Now, multiply both the numerator and the denominator of 5/16 by 6.25:
5 × 6.25 = 31.25 16 × 6.25 = 100
Therefore, 5/16 is equal to 31.25/100, which is equivalent to 31.25%.
Method 2: Using Decimal Conversion
Another common method involves converting the fraction to a decimal first and then multiplying by 100 to express it as a percentage. Let's start with the original fraction 25/80:
Divide the numerator (25) by the denominator (80):
25 ÷ 80 = 0.3125
Now, multiply the decimal by 100 to convert it to a percentage:
0.3125 × 100 = 31.25
Therefore, 25/80 is equal to 31.25%. This method is often preferred for its simplicity and ease of use with a calculator.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We can set up a proportion to solve for the percentage:
x/100 = 25/80
To solve for x (the percentage), we cross-multiply:
80x = 2500
Now, divide both sides by 80:
x = 2500 ÷ 80 = 31.25
Therefore, 25/80 is equivalent to 31.25%.
Mathematical Explanation: Why it Works
The core principle behind converting fractions to percentages lies in the concept of equivalent fractions. A percentage is simply a fraction where the denominator is always 100. The process we've used involves finding an equivalent fraction to the original fraction (25/80) that has a denominator of 100. This equivalent fraction directly represents the percentage. Whether we simplify first or use decimal conversion, we ultimately achieve the same result: expressing the portion represented by the fraction as a value out of 100.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in a wide range of real-world applications:
- Financial calculations: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Data analysis and statistics: Representing proportions in data sets, interpreting survey results, and understanding statistical significance.
- Everyday scenarios: Determining tips in restaurants, calculating sales tax, understanding discounts, and comparing prices.
- Academic settings: Solving problems related to ratios, proportions, and probabilities.
- Scientific fields: Expressing concentrations, experimental results, and error margins.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator for these calculations?
A1: Absolutely! Calculators are highly efficient for converting fractions to decimals and then to percentages. Simply divide the numerator by the denominator and then multiply the result by 100.
Q2: What if the fraction doesn't simplify easily?
A2: Even if the fraction doesn't simplify neatly, you can still use the decimal conversion method or the proportion method. These methods work regardless of the complexity of the fraction.
Q3: What does it mean if the percentage is greater than 100%?
A3: A percentage greater than 100% means that the numerator is larger than the denominator in the original fraction. This signifies that the part being represented is greater than the whole, which is often encountered in scenarios like growth or increase.
Q4: How can I improve my understanding of percentage calculations?
A4: Practice is key! Try solving various problems with different fractions, and utilize different methods to build your confidence and fluency. Online resources and practice exercises can be incredibly helpful.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with numerous practical applications. We've explored three distinct methods for converting 25/80 to a percentage—direct conversion, decimal conversion, and using proportions—and demonstrated that they all yield the same result: 31.25%. By understanding these methods and their underlying principles, you can confidently tackle percentage calculations in various contexts. Remember to practice regularly to master this essential skill and enhance your mathematical abilities. The ability to understand and work with percentages is a valuable tool that will serve you well throughout your academic and professional life.
Latest Posts
Latest Posts
-
Probability Replacement And Without Replacement
Sep 12, 2025
-
What Makes An Experiment Valid
Sep 12, 2025
-
The Emperors New Clothes Moral
Sep 12, 2025
-
Transparent And Translucent And Opaque
Sep 12, 2025
-
Hydrochloric Acid Sodium Thiosulphate
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 25 80 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.