2x X 2 X 2
catronauts
Sep 13, 2025 · 7 min read
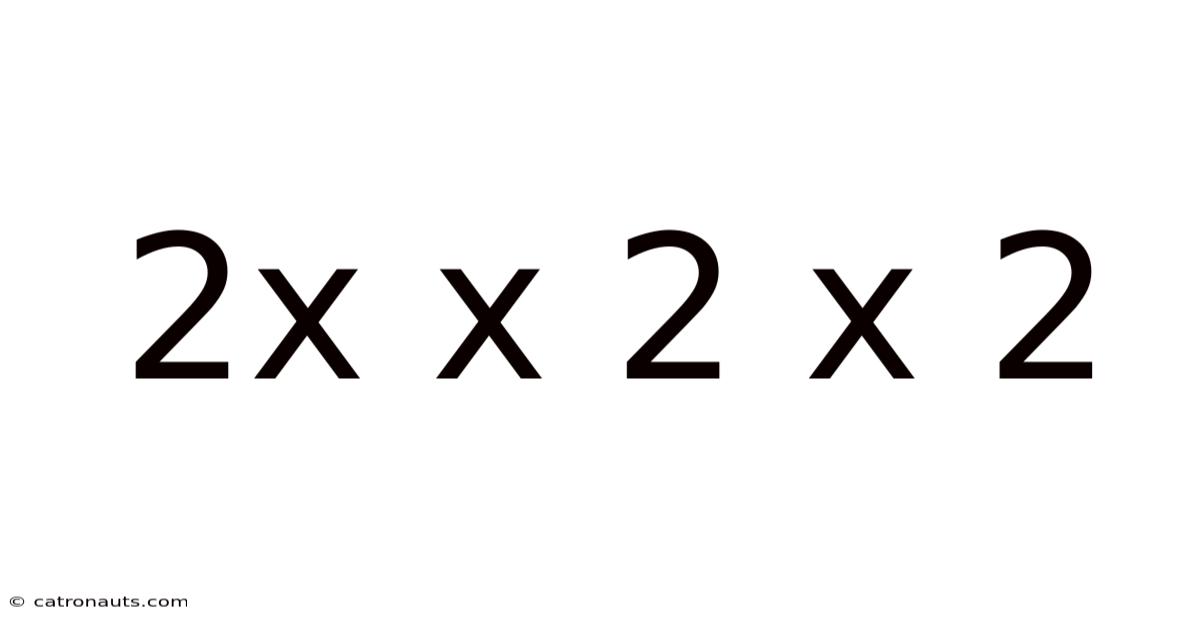
Table of Contents
Decoding 2 x 2 x 2: Exploring the Mathematical, Scientific, and Philosophical Implications of Cubic Doubling
This article delves into the seemingly simple mathematical expression "2 x 2 x 2," exploring its significance beyond basic arithmetic. We'll uncover its implications across various fields, from its fundamental role in mathematics and computer science to its surprising appearances in scientific models and even philosophical discussions about growth and complexity. Understanding this seemingly simple equation unlocks a door to a deeper appreciation of exponential growth and its impact on our world.
Introduction: Beyond the Obvious 8
At its most basic level, 2 x 2 x 2 equals 8. This straightforward calculation is taught in elementary school, a cornerstone of arithmetic understanding. However, the significance of this equation transcends its immediate answer. It represents the foundational concept of cubic growth, a powerful force that shapes everything from the spread of information to the complexity of biological systems. This exploration will unpack the multifaceted implications of this deceptively simple equation, revealing its hidden depths and profound impact.
The Mathematical Foundation: Cubing and Exponential Growth
Mathematically, 2 x 2 x 2 represents the cube of the number 2. Cubing a number means multiplying it by itself three times. This operation is distinct from squaring (multiplying a number by itself twice), resulting in a vastly different rate of growth. While squaring leads to quadratic growth, cubing leads to exponential growth. This difference is crucial. Quadratic growth increases relatively slowly, while exponential growth accelerates dramatically, leading to incredibly large numbers in a relatively short time.
Consider the sequence: 2, 4, 8, 16, 32, 64... This sequence demonstrates exponential growth. Each number is double the previous one. The equation 2 x 2 x 2 represents the third term in this sequence, highlighting the rapid increase characteristic of exponential growth. This principle is fundamental to various mathematical concepts, including geometric series, compound interest, and the study of recursive functions.
Applications in Computer Science: Binary and Data Structures
The number 8, the result of 2 x 2 x 2, holds a special place in computer science. Computers operate on a binary system, a base-2 number system using only 0 and 1. A single binary digit (bit) can represent two states (0 or 1). Combining eight bits forms a byte, a fundamental unit of data storage. The equation 2 x 2 x 2 directly reflects the structure of a byte: 2 bits x 2 bits x 2 bits = 8 bits (1 byte). This seemingly simple calculation underpins the entire digital world, enabling the storage and processing of vast amounts of information.
Furthermore, the concept of cubic growth is relevant to the efficiency and scalability of algorithms and data structures. For instance, the time complexity of certain algorithms can increase cubically with the size of the input data. Understanding cubic growth allows computer scientists to design more efficient algorithms and data structures, crucial for handling increasingly large datasets in applications ranging from scientific simulations to machine learning.
Scientific Manifestations: Volume, Density, and Biological Growth
In the physical world, the equation 2 x 2 x 2 finds its expression in the calculation of volume. Imagine a cube with sides of length 2 units. The volume of this cube is 2 x 2 x 2 = 8 cubic units. This simple formula extends to any cube, demonstrating the relationship between linear dimensions and volume. This principle is fundamental in various scientific fields, including:
- Physics: Calculating the volume of objects is essential in various physics problems, from fluid mechanics to thermodynamics.
- Chemistry: The volume of containers and the space occupied by molecules play a vital role in chemical reactions and calculations.
- Biology: Cellular growth and the volume of biological structures often exhibit relationships related to cubic growth.
Beyond volume, the concept of cubic growth is also relevant to density. Density is mass per unit volume. If the mass of an object increases cubically while its volume increases linearly, the density will change significantly. This interplay between volume and density has important implications for various biological processes and materials science.
Beyond the Numbers: Philosophical Implications of Exponential Growth
The rapid acceleration inherent in exponential growth, as represented by 2 x 2 x 2, raises profound philosophical questions. Consider the implications for:
- Technological Advancement: Moore's Law, which states that the number of transistors on a microchip doubles approximately every two years, is a prime example of exponential growth in technology. This rapid advancement has dramatically altered our world, raising questions about the long-term consequences of such exponential progress.
- Population Growth: Human population growth, while not perfectly exponential, has shown periods of rapid increase, raising concerns about resource depletion and environmental sustainability. Understanding exponential growth helps us better model and address these challenges.
- Information Spread: The spread of information in the digital age often follows exponential patterns. Viral videos, news stories, and social media trends can rapidly gain traction, showcasing the powerful impact of exponential growth in communication.
These examples highlight the ethical and societal implications of exponential growth. While such growth can be beneficial, leading to technological advancements and economic prosperity, it also presents challenges that require careful consideration and proactive solutions. Understanding the mathematical underpinnings of exponential growth allows for a more informed and nuanced approach to managing its effects.
Exploring Further: Higher Dimensions and Beyond
The equation 2 x 2 x 2 can be considered a specific case of a more general principle: the calculation of hypervolumes in higher dimensions. While we can easily visualize a cube (three dimensions), extending this to four or more dimensions becomes more abstract. However, the mathematical principles remain consistent. The volume of a hypercube in n dimensions with side length 2 would be 2<sup>n</sup>.
This extension into higher dimensions highlights the mathematical elegance and generality of the fundamental concept. It transcends the simple visualization of a cube and opens the door to exploring more complex mathematical structures and their applications in various scientific fields.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 2 x 2 x 2 and 2<sup>3</sup>?
- A: They are mathematically equivalent. 2<sup>3</sup> (2 raised to the power of 3) is simply a more concise way of writing 2 x 2 x 2.
-
Q: Are there real-world examples of perfect cubic growth?
- A: While perfectly consistent cubic growth is rare in natural systems, many processes exhibit approximate cubic growth patterns, particularly over limited time scales. Examples include the volume of a growing crystal or the initial spread of a disease in a susceptible population.
-
Q: How can understanding 2 x 2 x 2 help me in my daily life?
- A: While you might not directly use the calculation every day, understanding the concept of exponential growth provides a valuable framework for thinking about various situations. It can help in making financial decisions, planning for the future, and understanding the dynamics of various systems in the world around you.
-
Q: What are some further areas of study related to exponential growth?
- A: Further exploration could involve studying calculus (particularly exponential functions and derivatives), the study of algorithms and data structures in computer science, population dynamics in ecology, and the mathematical modelling of various complex systems.
Conclusion: The Enduring Significance of a Simple Equation
The seemingly simple equation 2 x 2 x 2, while resulting in the straightforward answer of 8, reveals a wealth of significance across various disciplines. From its foundational role in mathematics and computer science to its manifestations in scientific models and philosophical discussions, this equation represents a powerful concept: exponential growth. Understanding this concept allows for a deeper appreciation of the dynamics of various systems, from the inner workings of computers to the challenges posed by population growth and technological advancement. The enduring significance of this simple equation lies not just in its numerical result but in the profound implications of the underlying principle of exponential growth. By exploring this equation, we gain a more comprehensive understanding of the world around us and the powerful forces shaping our future.
Latest Posts
Latest Posts
-
How Many Minutes Until 11
Sep 13, 2025
-
Graph Of Function And Derivative
Sep 13, 2025
-
What Is An Interlude Music
Sep 13, 2025
-
1 Tbsp Yeast In Grams
Sep 13, 2025
-
Animals In A Coniferous Forest
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2x X 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.