3 4 Cups Times 4
catronauts
Sep 15, 2025 · 5 min read
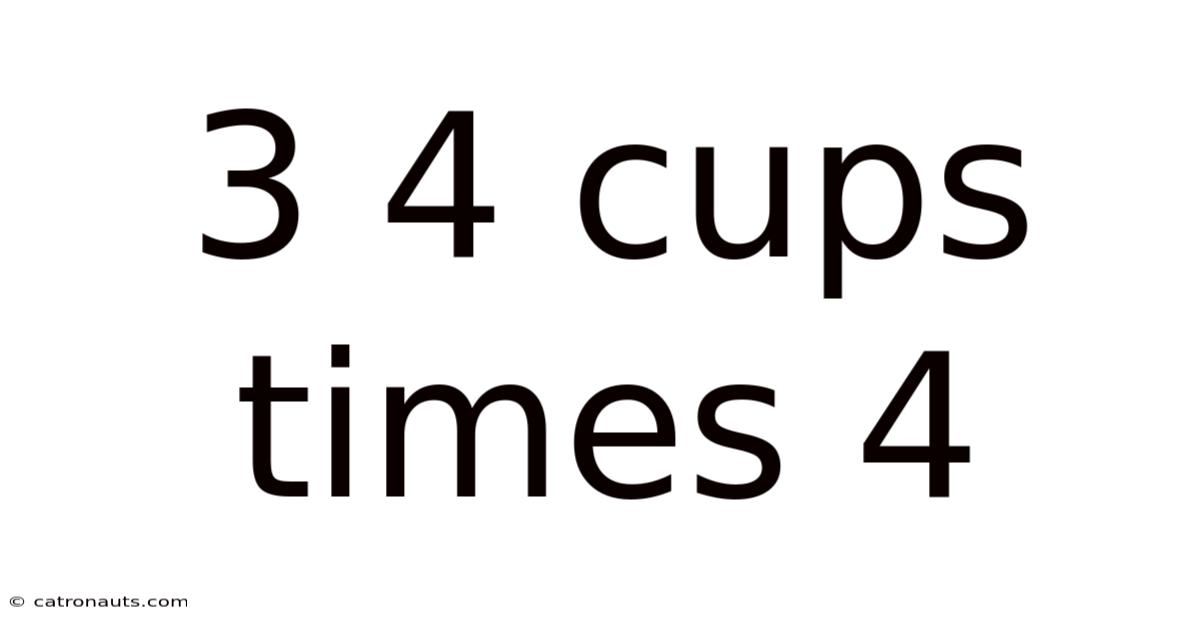
Table of Contents
Decoding the Simple, Yet Profound: 3 ¼ Cups Times 4
Understanding basic arithmetic is fundamental to countless aspects of our daily lives, from cooking and baking to budgeting and construction. This seemingly simple calculation – 3 ¼ cups times 4 – serves as a perfect microcosm of how these fundamental skills are applied. This article will not only solve this specific problem but also explore the underlying mathematical concepts, providing a deeper understanding of fractions, multiplication, and their real-world applications. We’ll delve into different approaches to solving the problem, catering to various learning styles and mathematical backgrounds. By the end, you'll not only know the answer but also possess a firmer grasp of fractional arithmetic.
Understanding the Problem: 3 ¼ Cups Times 4
The problem "3 ¼ cups times 4" asks us to determine the total volume obtained when we combine four identical quantities, each measuring 3 ¼ cups. This type of problem frequently appears in recipes (scaling up a dish), construction (calculating material needs), and various other scenarios demanding accurate measurements. The key to solving this lies in our understanding of fractions and their interaction with whole numbers during multiplication.
Method 1: Converting to Improper Fractions
This method leverages the power of converting mixed numbers (like 3 ¼) into improper fractions. An improper fraction has a numerator larger than its denominator. This format simplifies multiplication.
Step 1: Convert the mixed number to an improper fraction.
To convert 3 ¼ to an improper fraction, we multiply the whole number (3) by the denominator (4), add the numerator (1), and keep the same denominator:
(3 x 4) + 1 = 13
Therefore, 3 ¼ becomes 13/4.
Step 2: Multiply the improper fraction by 4.
Now, we multiply the improper fraction by 4:
(13/4) x 4 = 13
Step 3: Interpret the Result.
The result, 13, represents 13 cups. Therefore, 3 ¼ cups times 4 equals 13 cups.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this to solve our problem by breaking down 3 ¼ into its whole number and fractional parts.
Step 1: Separate the whole number and fraction.
We can rewrite 3 ¼ as 3 + ¼.
Step 2: Apply the distributive property.
Now, we multiply 4 by each part separately:
4 x (3 + ¼) = (4 x 3) + (4 x ¼)
Step 3: Solve the individual multiplications.
(4 x 3) = 12 (4 x ¼) = 1
Step 4: Combine the results.
Adding the results together: 12 + 1 = 13
Therefore, 3 ¼ cups times 4 equals 13 cups.
Method 3: Decimal Conversion
This method involves converting the mixed number into a decimal before performing the multiplication. While seemingly simpler, it can introduce rounding errors in some cases, especially with more complex fractions.
Step 1: Convert the fraction to a decimal.
¼ is equivalent to 0.25.
Step 2: Convert the mixed number to a decimal.
3 ¼ becomes 3 + 0.25 = 3.25
Step 3: Multiply the decimal by 4.
3.25 x 4 = 13
Therefore, 3 ¼ cups times 4 equals 13 cups.
Visualizing the Problem: A Practical Approach
Imagine you're baking a cake and the recipe calls for 3 ¼ cups of flour. You need to quadruple the recipe to make four cakes. Using any of the above methods, you'd determine you need a total of 13 cups of flour. This visual representation helps ground the abstract mathematical concepts in a tangible, real-world context.
Why Understanding Fractions is Crucial
The ability to work comfortably with fractions is paramount in numerous fields. From culinary arts and construction to finance and engineering, precise measurements and calculations involving fractions are essential for accuracy and success. The example of multiplying 3 ¼ cups by 4 highlights the everyday relevance of fractional arithmetic. Mastering this skill builds a strong foundation for more advanced mathematical concepts.
Expanding the Concept: Scaling Recipes and Beyond
The principles illustrated here directly apply to scaling recipes. Whether you're doubling, tripling, or quadrupling a recipe, understanding how to multiply mixed numbers and fractions is crucial for achieving consistent results. This extends beyond cooking; similar calculations are necessary in various fields where precise measurements are critical.
Troubleshooting Common Mistakes
A frequent mistake when dealing with fractions is incorrectly converting mixed numbers to improper fractions or incorrectly applying the distributive property. Always double-check your calculations and ensure you are following the correct steps. Practice is key to mastering these techniques and avoiding errors.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction multiplication. However, understanding the underlying mathematical principles is still valuable for developing problem-solving skills and avoiding reliance on technology in situations where a calculator might not be available.
Q: What if the problem involved a more complex fraction?
A: The same principles apply. Convert mixed numbers to improper fractions, use the distributive property, or convert to decimals (bearing in mind potential rounding errors). The steps remain consistent, although the calculations might become more involved.
Q: Are there other ways to solve this type of problem?
A: While the methods presented are the most common and efficient, there are alternative approaches, such as repeated addition (adding 3 ¼ four times). This is less efficient for larger numbers but can be helpful for visualization and understanding the concept.
Q: Why is it important to learn multiple methods for solving this problem?
A: Learning different methods provides flexibility and a deeper understanding of the underlying mathematical principles. Different methods might be more suitable depending on the specific problem and individual preferences.
Conclusion: Mastering the Fundamentals
Solving "3 ¼ cups times 4" might seem trivial at first glance. However, unraveling this simple problem reveals the fundamental importance of understanding fractions, mixed numbers, and the various methods for multiplying them. These skills are indispensable in a wide array of practical applications, highlighting the significance of mastering basic arithmetic for success in various endeavors. By understanding and practicing the methods outlined, you build not just a solution to this specific problem but a broader mathematical competency applicable to countless future challenges. The key takeaway is that even seemingly simple arithmetic problems offer opportunities for deep learning and practical application, emphasizing the value of a strong foundational understanding of mathematical principles.
Latest Posts
Latest Posts
-
Translate The Book In Spanish
Sep 15, 2025
-
How To Divide With Integers
Sep 15, 2025
-
Villa Of The Mysteries Pompeii
Sep 15, 2025
-
Division Of Fractions Problem Solving
Sep 15, 2025
-
Twin Tower Hotel Kuala Lumpur
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Cups Times 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.