39 45 As A Percentage
catronauts
Sep 13, 2025 · 5 min read
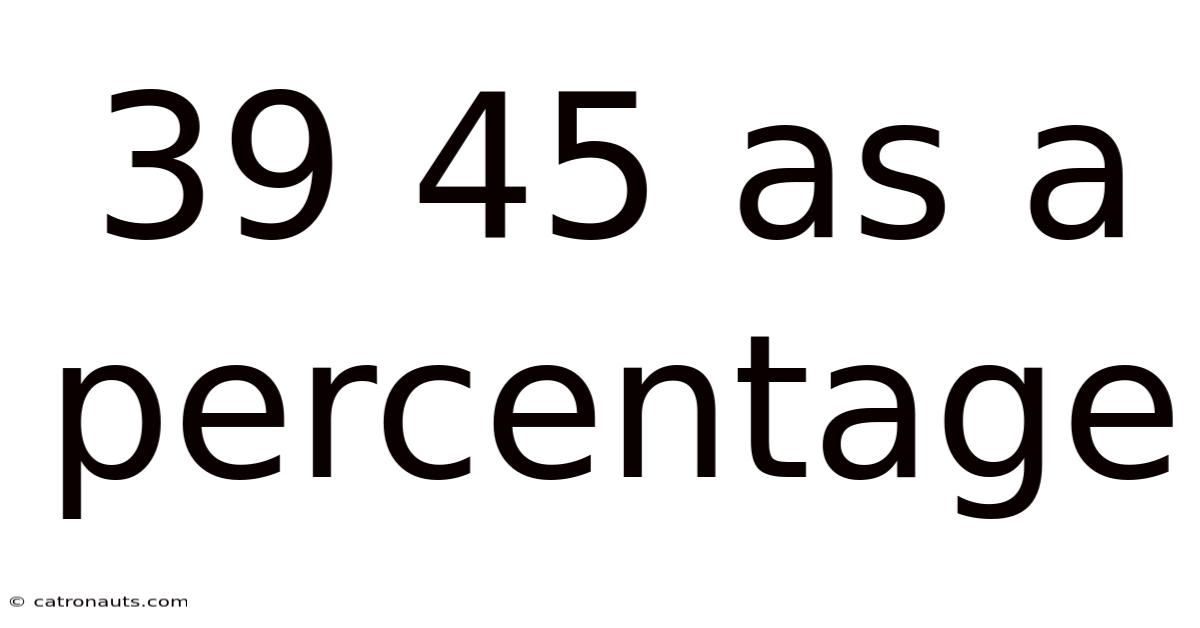
Table of Contents
Decoding 39 out of 45: A Comprehensive Guide to Percentage Calculation and Interpretation
Understanding percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis and everyday decision-making. This article delves deep into the calculation and interpretation of "39 out of 45" as a percentage, exploring the underlying mathematical principles, providing step-by-step instructions, and addressing common misconceptions. We'll also examine practical applications and explore how to present this information effectively. This comprehensive guide will empower you to confidently calculate and understand percentages in various contexts.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. It represents a proportion or ratio out of a whole. The symbol "%" is used to denote a percentage. For example, 50% means 50 out of 100, or one-half. Understanding percentages is crucial for interpreting data, comparing values, and making informed decisions.
The core concept behind percentage calculation involves establishing a ratio between a part and a whole, then scaling this ratio to express it as a fraction of 100. In the case of "39 out of 45," 39 represents the part and 45 represents the whole.
Calculating 39 out of 45 as a Percentage: A Step-by-Step Guide
To calculate 39 out of 45 as a percentage, follow these steps:
-
Establish the Ratio: The ratio of the part to the whole is 39/45.
-
Convert to Decimal: Divide the part (39) by the whole (45): 39 ÷ 45 = 0.866666...
-
Convert Decimal to Percentage: Multiply the decimal by 100: 0.866666... × 100 = 86.6666...%
-
Round to Desired Precision: Depending on the context, round the percentage to a suitable number of decimal places. For example, rounding to two decimal places gives 86.67%. Rounding to the nearest whole number gives 87%.
Therefore, 39 out of 45 is 86.67% (rounded to two decimal places).
Understanding the Result: Interpretation and Context
The calculated percentage, 86.67%, signifies that 39 represents approximately 87% of 45. This high percentage suggests a strong performance or a significant proportion. However, the interpretation depends heavily on the context.
-
Academic Performance: If 39 out of 45 represents a student's score on a test, 86.67% indicates a very good performance, likely earning a high grade.
-
Survey Results: If 39 out of 45 respondents answered "yes" to a survey question, this represents strong agreement or support for the topic.
-
Production Efficiency: If 39 out of 45 products passed quality control, the percentage suggests a high production efficiency with a low defect rate.
The context dictates the significance of the percentage. A 86.67% success rate in one area might be exceptional, while in another it might be considered average or even poor.
Alternative Calculation Methods
While the method above is straightforward, there are alternative approaches to calculating percentages.
-
Using a Calculator: Most calculators have a percentage function (%) which simplifies the calculation. Simply input 39 ÷ 45 and then press the % key.
-
Using Spreadsheet Software: Programs like Microsoft Excel or Google Sheets offer built-in functions for percentage calculations. The formula
=39/45will return the decimal value, and formatting the cell as a percentage will display the result as 86.67%. -
Mental Estimation: For quick estimations, you can round the numbers. For example, rounding 39 to 40 and 45 to 45 simplifies the calculation: 40/45 ≈ 0.89, which is approximately 89%. This offers a reasonably accurate quick estimation.
Advanced Concepts: Error Margins and Statistical Significance
When dealing with percentages, particularly in statistical contexts, it’s essential to consider error margins and statistical significance. A 86.67% success rate doesn't necessarily mean that the true underlying success rate is precisely 86.67%. There's always a margin of error associated with sample data.
For example, if this data represents a sample from a larger population, statistical methods can be used to calculate a confidence interval, which provides a range of values within which the true percentage likely lies. This range accounts for the inherent uncertainty in using sample data to infer properties of the larger population. The sample size (45 in this case) also influences the precision of the estimate.
Common Misconceptions about Percentages
Several common misconceptions surround percentage calculations:
-
Adding Percentages Directly: It's incorrect to simply add percentages without considering the underlying base values. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Misunderstanding the "Whole": Always clearly define the "whole" when working with percentages. The "whole" is the reference point against which the part is compared.
-
Interpreting Percentages Without Context: The meaning of a percentage is heavily context-dependent. A high percentage in one situation might be low in another.
Frequently Asked Questions (FAQ)
Q1: How can I calculate a percentage increase or decrease?
To calculate a percentage increase or decrease, first find the difference between the new and old values. Then divide this difference by the old value and multiply by 100. For example, if a value increases from 50 to 60, the percentage increase is (60-50)/50 * 100 = 20%.
Q2: What is the difference between percentage points and percentages?
Percentage points refer to the absolute difference between two percentages, while percentages represent a proportional change. For example, if a value increases from 50% to 60%, the percentage increase is 20%, but the increase in percentage points is 10.
Q3: Can I express a percentage as a fraction or a decimal?
Yes, percentages can be easily converted to fractions or decimals. To convert a percentage to a decimal, divide by 100. To convert a percentage to a fraction, write the percentage as the numerator and 100 as the denominator, then simplify. For example, 86.67% = 0.8667 = 8667/10000.
Q4: How do I reverse a percentage calculation?
To find the original value after a percentage change, you can use algebraic methods. For example, if a value is increased by 10% to reach 110, the original value was 110 / 1.10 = 100.
Conclusion: Mastering Percentage Calculations
Understanding and calculating percentages is a vital skill across various aspects of life. This article provides a comprehensive guide to calculating 39 out of 45 as a percentage, explaining the underlying principles and addressing common misconceptions. Remember that the interpretation of a percentage depends entirely on its context. By mastering percentage calculations and applying critical thinking, you can effectively analyze data, make informed decisions, and communicate your findings clearly. Remember to always consider the context, potential error margins, and the significance of your results when working with percentages.
Latest Posts
Latest Posts
-
My Name Is In Germany
Sep 13, 2025
-
Formal Assessment And Informal Assessment
Sep 13, 2025
-
Convert 42 C To F
Sep 13, 2025
-
Elements To Form A Contract
Sep 13, 2025
-
World Map With Hong Kong
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 39 45 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.