3x 2 X 2 0
catronauts
Sep 19, 2025 · 6 min read
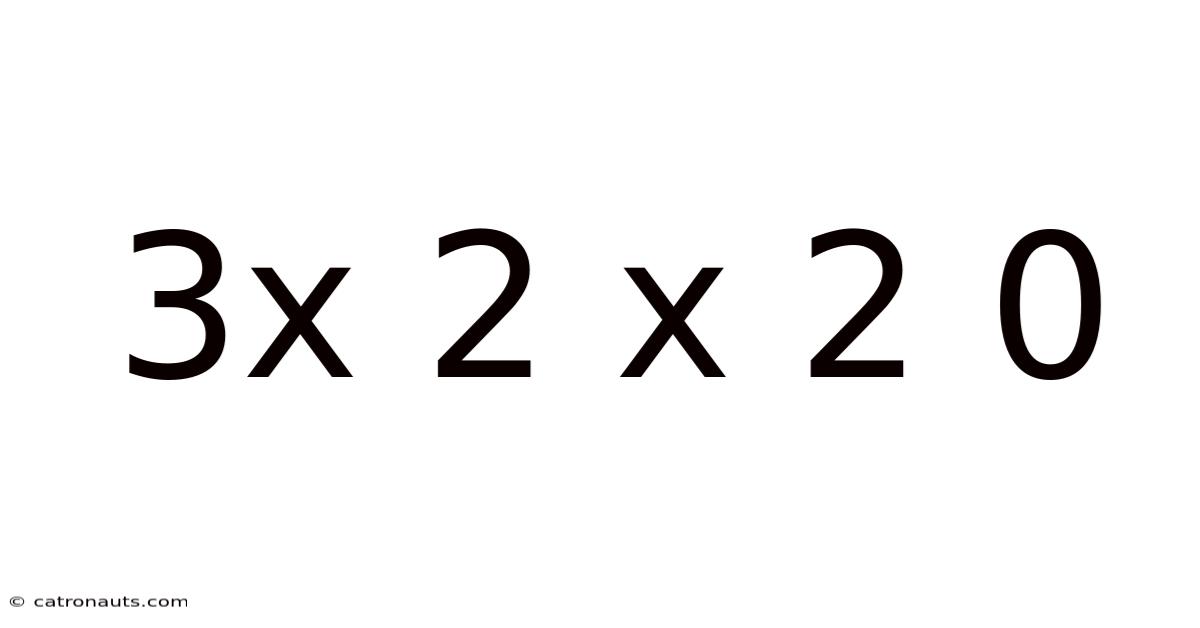
Table of Contents
Decoding 3 x 2 x 20: Exploring the Intrigue of a Numerical Expression
This article delves into the seemingly simple numerical expression "3 x 2 x 20," exploring its various interpretations, potential applications, and the broader mathematical concepts it touches upon. While the calculation itself is straightforward, understanding its implications offers valuable insights into fundamental arithmetic operations and their significance across diverse fields. We'll dissect the expression, explore its applications in different contexts, and even examine some common misconceptions surrounding similar expressions. This detailed exploration will aim to provide a comprehensive understanding, making it a valuable resource for students, educators, and anyone curious about the fascinating world of numbers.
Understanding the Fundamentals: Order of Operations (PEMDAS/BODMAS)
Before diving into the intricacies of 3 x 2 x 20, it's crucial to understand the order of operations. This fundamental principle ensures consistency in mathematical calculations, regardless of the complexity of the expression. Remember the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same hierarchical order in which operations should be performed.
In our example, "3 x 2 x 20," we only have multiplication operations. According to PEMDAS/BODMAS, these operations are performed from left to right. Therefore, the calculation is performed as follows:
- 3 x 2 = 6
- 6 x 20 = 120
Therefore, the solution to 3 x 2 x 20 is 120. This seemingly simple calculation forms the foundation for more complex mathematical problems.
Applications of Multiplication and its Significance
The core operation in "3 x 2 x 20" is multiplication. Understanding its practical applications is key to grasping the significance of this seemingly simple expression. Multiplication is fundamental to many areas of life, including:
-
Everyday calculations: From calculating the total cost of multiple items to determining the area of a rectangle, multiplication is an indispensable tool in our daily lives. Imagine calculating the total cost of 20 items priced at $6 each (20 x $6 = $120), mirroring the logic in our original expression.
-
Engineering and physics: In engineering and physics, multiplication is crucial for calculations involving forces, distances, velocities, and many other physical quantities. For instance, calculating the total energy consumption based on wattage and time utilizes multiplication.
-
Finance and economics: Calculating interest, profits, and losses often involves repeated multiplication. Understanding compound interest, for example, requires proficiency in multiplication and exponential growth.
-
Computer science: In computer science, multiplication is a fundamental operation used in various algorithms and data structures. Matrix multiplications, for example, are crucial in various applications of computer graphics and machine learning.
-
Statistics and probability: Many statistical calculations rely heavily on multiplication. Calculating probabilities, for example, often involves multiplying probabilities of independent events.
Expanding the Concept: Introducing Variables and Equations
While "3 x 2 x 20" is a simple numerical expression, we can expand the concept by introducing variables. Let's say:
a = 3b = 2c = 20
Our expression can then be rewritten as: a x b x c = 120. This simple substitution opens up possibilities for algebraic manipulation and problem-solving. We can now explore different scenarios by changing the values of a, b, and c and examining how the result changes. This concept is essential in algebra and forms the basis for solving more complex equations.
Exploring Beyond the Basics: Factorials and Combinations
The expression "3 x 2 x 20" can also be used as a stepping stone to understand more advanced mathematical concepts. While not directly involved, the multiplication concept is fundamental to factorials and combinations.
-
Factorials: A factorial (denoted by !) is the product of all positive integers less than or equal to a given positive integer. For example, 3! = 3 x 2 x 1 = 6. Although our expression doesn't directly involve a factorial, the multiplicative nature is similar. Understanding factorials is vital in probability and combinatorics.
-
Combinations: Combinations are used to determine the number of ways to choose a subset from a larger set without considering the order. Calculating combinations often involves factorials and multiplication, highlighting the interconnectedness of mathematical concepts.
Addressing Potential Misconceptions: The Importance of Order
A common misconception in mathematics is neglecting the order of operations. Incorrectly performing calculations can lead to significantly different results. For instance, if we were to mistakenly perform the operations in a different order (e.g., 2 x 20 first), we would obtain a different, incorrect answer. Always adhering to the PEMDAS/BODMAS order is paramount for accuracy.
Practical Applications: Real-World Scenarios
Let's explore some practical scenarios where an understanding of the expression 3 x 2 x 20, and its underlying multiplicative principle, would be valuable:
-
Manufacturing: A factory produces 3 batches of a product daily, with each batch containing 2 sub-assemblies, and each sub-assembly requiring 20 components. The total number of components needed daily is 3 x 2 x 20 = 120.
-
Construction: A construction project uses 3 types of bricks, with 2 different colors available for each type and 20 bricks of each color needed. The total number of bricks required is 3 x 2 x 20 = 120.
-
Retail: A store sells 3 types of shirts, each in 2 sizes and 20 pieces per size. The total number of shirts available is 3 x 2 x 20 = 120.
Frequently Asked Questions (FAQ)
Q: What if the numbers were different? How would the calculation change?
A: The calculation would change based on the new numbers. The process remains the same: multiply the numbers from left to right, adhering to PEMDAS/BODMAS.
Q: Can this expression be simplified?
A: The expression can be simplified by performing the multiplication, resulting in the single value 120.
Q: Are there any other mathematical operations that could be applied here?
A: While multiplication is the primary operation here, other operations could be added if the expression were extended. For example, adding parentheses could alter the order of operations.
Q: How does this expression relate to more advanced mathematical concepts?
A: This simple expression forms a foundational block for understanding more complex concepts like algebra, calculus, and even abstract algebra, which deal with broader structures and relationships between numbers.
Conclusion: The Power of Simple Expressions
While the numerical expression "3 x 2 x 20" seems deceptively simple, its exploration reveals the fundamental importance of basic arithmetic operations, the power of order of operations, and the potential applications across numerous fields. Understanding this seemingly simple expression enhances our grasp of mathematical principles and their practical relevance in our daily lives. From calculating daily expenses to comprehending complex engineering designs, the ability to perform and understand simple mathematical calculations like this one forms a crucial stepping stone to a more profound understanding of the mathematical world. Remember, mastering the basics unlocks the door to exploring more complex and fascinating mathematical concepts.
Latest Posts
Latest Posts
-
Song Of The Lark Cather
Sep 19, 2025
-
Keratin What Does It Do
Sep 19, 2025
-
Fun Facts Of North America
Sep 19, 2025
-
Calcium Carbonate And Hcl Reaction
Sep 19, 2025
-
Words That Are Misspelled Often
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 X 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.