4 7 As A Percent
catronauts
Sep 12, 2025 · 6 min read
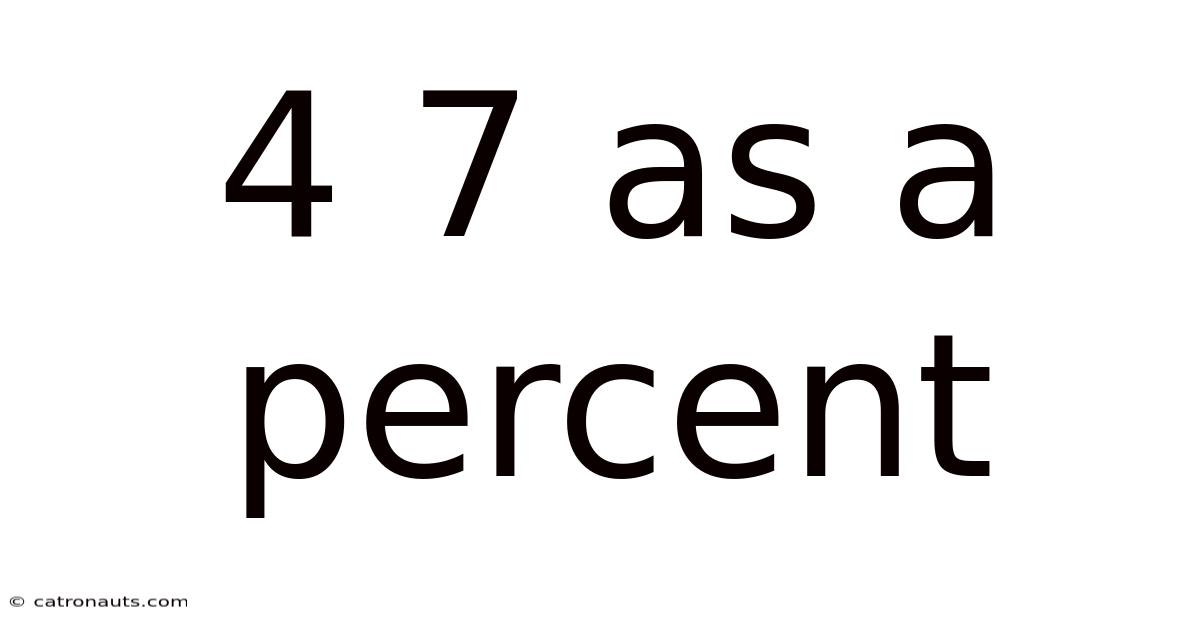
Table of Contents
Understanding 4/7 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics, crucial for various applications in daily life, from calculating discounts to understanding statistical data. This comprehensive guide will delve into the process of converting the fraction 4/7 into a percentage, explaining the steps involved, providing different calculation methods, and exploring related concepts. We will also delve into the practical applications and common misconceptions surrounding percentage calculations. Understanding 4/7 as a percentage isn't just about a single calculation; it's about mastering a core mathematical concept.
Introduction: Fractions, Decimals, and Percentages
Before we dive into calculating 4/7 as a percentage, let's briefly review the relationships between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Express a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 4/7 represents 4 parts out of a total of 7 parts.
-
Decimals: Express a part of a whole using a base-10 system, with a decimal point separating the whole number from the fractional part. For instance, 0.5 represents half (or 5/10).
-
Percentages: Express a part of a whole as a proportion of 100. The symbol "%" represents "per hundred," so 50% means 50 out of 100.
These three forms are interchangeable; you can convert any one of them into the other two. Understanding these relationships is crucial for working with mathematical problems involving proportions.
Method 1: Direct Conversion using Division
The most straightforward way to convert 4/7 to a percentage is through direct division. The fraction 4/7 indicates that we need to divide 4 by 7.
-
Perform the division: Divide 4 by 7 using a calculator or long division. This gives you a decimal value. 4 ÷ 7 ≈ 0.57142857...
-
Multiply by 100: To convert the decimal to a percentage, multiply the result by 100. 0.57142857... × 100 ≈ 57.142857...
-
Round to the desired precision: Since percentages are often rounded for practicality, we can round the result to a specific number of decimal places. Rounding to two decimal places, we get approximately 57.14%.
Therefore, 4/7 is approximately equal to 57.14%. Remember that this is an approximation because the decimal representation of 4/7 is a non-terminating decimal (it goes on forever).
Method 2: Using Proportions
Another way to approach this problem is by setting up a proportion. We know that a percentage is a fraction out of 100. So, we can set up the following proportion:
4/7 = x/100
Where 'x' represents the percentage we want to find.
To solve for 'x', we can cross-multiply:
7x = 400
x = 400/7
x ≈ 57.14
Therefore, again we arrive at approximately 57.14%. This method provides a clearer understanding of the underlying proportional relationship involved in percentage calculations.
Method 3: Converting to a Decimal First
This method involves an intermediate step of converting the fraction to a decimal before multiplying by 100.
-
Convert the fraction to a decimal: Divide the numerator (4) by the denominator (7) to obtain the decimal equivalent. 4 ÷ 7 ≈ 0.57142857...
-
Multiply by 100: Multiply the decimal by 100 to express it as a percentage. 0.57142857... × 100 ≈ 57.142857...
-
Round: Round the percentage to the desired number of decimal places. Rounding to two decimal places gives us 57.14%.
This method breaks down the process into smaller, manageable steps, making it easier to understand for beginners.
Understanding the Approximation
It’s crucial to understand that 57.14% is an approximation of 4/7. The decimal representation of 4/7 is a recurring decimal (0.571428571428...), meaning the digits repeat infinitely. Rounding is necessary for practical applications, but it introduces a small degree of error. The accuracy of the approximation depends on the number of decimal places you choose to retain.
Practical Applications of Percentage Calculations
Understanding percentage calculations, including converting fractions like 4/7 to percentages, is vital in numerous real-world situations:
-
Financial Calculations: Calculating discounts, interest rates, taxes, profit margins, and investment returns all involve percentages.
-
Statistical Analysis: Percentages are used extensively to represent proportions in data, such as survey results, population demographics, and economic indicators.
-
Scientific Applications: Percentages are used to express concentrations of solutions, reaction yields, and error margins in experiments.
-
Everyday Life: Understanding percentages helps you make informed decisions when comparing prices, evaluating deals, and understanding proportions in recipes or instructions.
Common Mistakes to Avoid
Several common mistakes can arise when converting fractions to percentages:
-
Incorrect order of operations: Remember to divide the numerator by the denominator before multiplying by 100.
-
Rounding errors: Be mindful of the level of accuracy required and round appropriately. Rounding too early can lead to significant errors in the final result.
-
Confusing percentages with decimals: Remember that a percentage is a fraction out of 100. You must multiply the decimal equivalent by 100 to get the percentage.
-
Not considering the context: Always consider the context of the problem. Understanding what the percentage represents is essential for accurate interpretation.
Frequently Asked Questions (FAQ)
Q: Is 4/7 exactly equal to 57.14%?
A: No, 57.14% is an approximation of 4/7. The exact decimal representation of 4/7 is a recurring decimal (0.57142857...), which means the digits repeat infinitely. 57.14% is a rounded approximation.
Q: How can I improve the accuracy of my approximation?
A: To improve accuracy, retain more decimal places during the calculation. However, for most practical purposes, rounding to two decimal places (57.14%) is sufficient.
Q: What if I have a more complex fraction?
A: The same method applies. Divide the numerator by the denominator and multiply the result by 100. For example, to convert 15/23 to a percentage, you would divide 15 by 23 and then multiply by 100.
Q: Are there any online tools to help with this conversion?
A: Yes, many online calculators and converters can perform fraction-to-percentage conversions. However, understanding the underlying mathematical principles is more important than relying solely on calculators.
Conclusion: Mastering Percentage Conversions
Converting fractions like 4/7 to percentages is a fundamental skill with wide-ranging applications. By understanding the different methods – direct division, proportions, and converting to decimals first – and avoiding common mistakes, you can confidently perform these conversions. Remember that while approximations are often necessary, it's crucial to understand the underlying mathematical principles and the limitations of rounding. The ability to perform these calculations accurately and efficiently is a valuable asset in various academic, professional, and everyday contexts. Mastering this concept empowers you to confidently navigate a wide range of numerical challenges.
Latest Posts
Latest Posts
-
Mass Flow To Volume Flow
Sep 12, 2025
-
Beauty And Beast Fairy Tale
Sep 12, 2025
-
Format Of Changes In Equity
Sep 12, 2025
-
Quotes From Twelve Angry Men
Sep 12, 2025
-
Map Of Straits Of Hormuz
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 4 7 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.