5 12 As A Percent
catronauts
Sep 19, 2025 · 6 min read
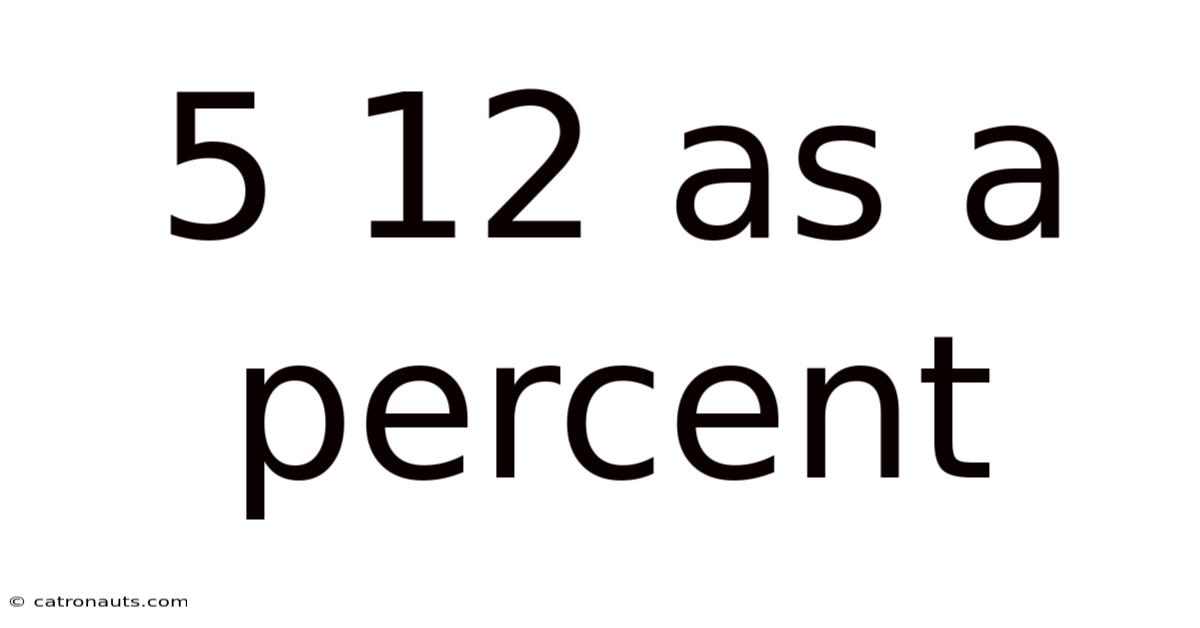
Table of Contents
Decoding 5/12 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This article will provide a thorough explanation of how to convert the fraction 5/12 into a percentage, exploring different methods and delving into the underlying mathematical concepts. We'll also address common questions and misconceptions related to percentage calculations. By the end, you'll not only know the answer but also understand the process deeply, empowering you to tackle similar problems with confidence.
Understanding Fractions and Percentages
Before diving into the conversion of 5/12, let's briefly review the fundamental concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage is to divide the numerator by the denominator and then multiply the result by 100. Let's apply this to the fraction 5/12:
-
Divide the numerator by the denominator: 5 ÷ 12 = 0.416666... (The result is a recurring decimal)
-
Multiply the result by 100: 0.416666... × 100 = 41.6666...%
Therefore, 5/12 is approximately 41.67%. We typically round the percentage to two decimal places for practicality.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction with a denominator of 100. This method relies on the principle that multiplying or dividing both the numerator and denominator of a fraction by the same number does not change its value. While this method is conceptually simple, it's not always practical, especially with fractions that don't easily convert to a denominator of 100.
To attempt this with 5/12, we need to find a number that, when multiplied by 12, results in 100. However, there is no whole number that satisfies this condition. We can, however, find an approximate equivalent:
-
Find a close multiple of 12: The closest multiples of 12 to 100 are 96 (12 x 8) and 108 (12 x 9).
-
Approximate the fraction: We can use either 8/8 (resulting in 40/96 which is close to 41.66%) or an approximation closer to 100/12 which then we divide.
This method shows the limitation when the denominator doesn't readily produce an equivalent fraction with 100 as its denominator. This method is less precise than direct division.
Method 3: Using Proportions
The concept of proportions offers another pathway to solve this problem. A proportion is a statement that two ratios are equal. We can set up a proportion to find the equivalent percentage:
5/12 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we can cross-multiply:
12x = 500
x = 500/12
x ≈ 41.67
This method demonstrates the equivalence between fractions and percentages through the concept of proportional relationships. It's a more algebraic approach compared to the direct division method.
Understanding the Recurring Decimal
It's important to note that the result of 5 ÷ 12 (0.416666...) is a recurring decimal. This means that the digit "6" repeats infinitely. When converting to a percentage, we usually round the decimal to a practical number of decimal places, such as two decimal places (41.67%). The level of precision required depends on the context of the problem. In many real-world applications, rounding to two decimal places is sufficient.
Practical Applications of Percentage Conversions
Converting fractions to percentages is a skill with widespread real-world applications:
-
Calculating Discounts: A store offers a 5/12 discount on an item. Converting 5/12 to 41.67% allows for easy calculation of the discount amount.
-
Understanding Financial Reports: Financial statements often express various ratios as fractions. Converting these fractions to percentages makes it easier to analyze financial performance.
-
Analyzing Statistical Data: Statistical data often involves working with fractions. Converting fractions to percentages makes the data more accessible and easier to interpret.
-
Assessing Test Scores: If you answered 5 out of 12 questions correctly on a test, converting 5/12 to a percentage (41.67%) gives you a clearer understanding of your performance.
-
Working with recipes: If a recipe calls for 5/12 of a cup of flour, knowing the percentage (41.67%) can be helpful in scaling the recipe.
Frequently Asked Questions (FAQ)
Q: Why do we multiply by 100 when converting a fraction to a percentage?
A: A percentage is a fraction out of 100. Multiplying by 100 scales the fraction to express it as a part of 100, making it a percentage.
Q: What if the fraction is greater than 1?
A: If the fraction is greater than 1 (e.g., 12/5), the resulting percentage will be greater than 100%. The same methods apply; you divide the numerator by the denominator and multiply by 100.
Q: Is there a specific method that is always the best?
A: The direct division method is generally the most efficient and reliable, especially when dealing with fractions that don't easily convert to an equivalent fraction with a denominator of 100. However, understanding the other methods provides a more holistic grasp of the underlying mathematical concepts.
Q: How accurate should my answer be?
A: The required accuracy depends on the context. For most everyday applications, rounding to two decimal places is sufficient. However, in scientific or engineering contexts, greater precision might be necessary.
Conclusion
Converting 5/12 to a percentage is a straightforward process that can be accomplished using several different methods. The direct division method, where you divide the numerator by the denominator and then multiply by 100, is often the most efficient. Remember that understanding the underlying principles of fractions and percentages is crucial for mastering this skill and applying it effectively in various situations. This knowledge isn't just about solving mathematical problems; it's about developing a deeper understanding of numerical relationships and their practical applications in the world around us. The ability to confidently convert fractions to percentages is a valuable asset in navigating everyday life and tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
Fight In The Past Tense
Sep 19, 2025
-
Things That Rhyme With Teacher
Sep 19, 2025
-
Non Keratinized Stratified Squamous Epithelium
Sep 19, 2025
-
Difference Between Too And To
Sep 19, 2025
-
What Is Automated Valuation Model
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.