5 Percent Of 500 000
catronauts
Sep 12, 2025 · 5 min read
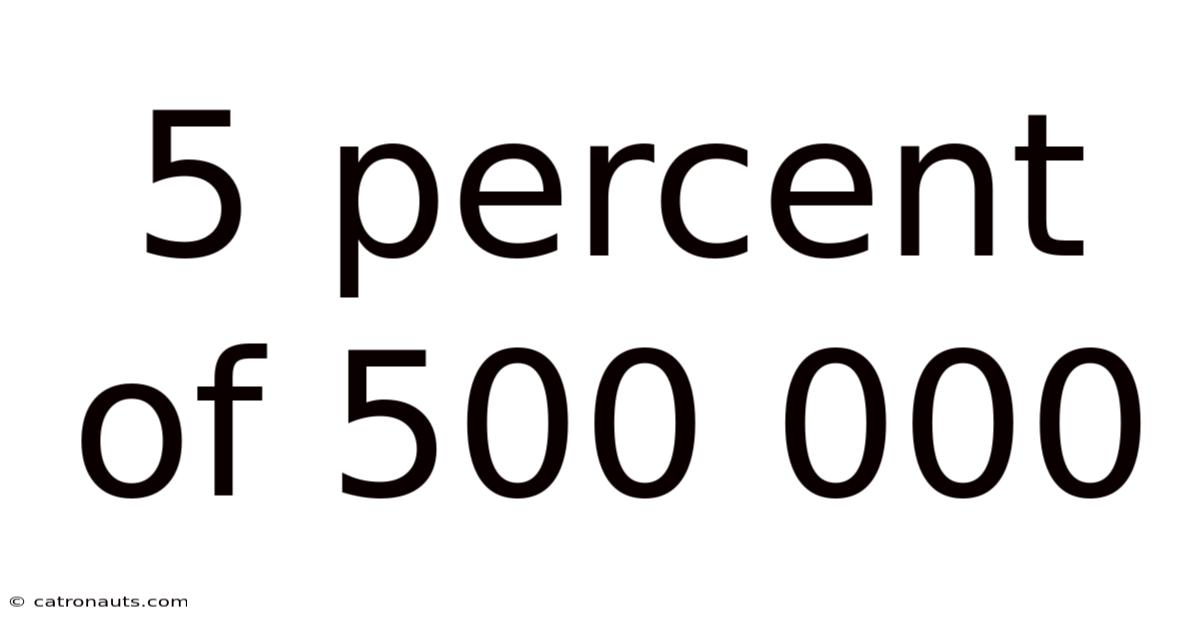
Table of Contents
Decoding 5 Percent of 500,000: A Deep Dive into Percentages and Their Applications
Finding 5 percent of 500,000 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying principles of percentages and their practical applications extends far beyond this basic calculation. This article will not only show you how to calculate 5% of 500,000 but also explore the broader context of percentages, their significance in various fields, and common misconceptions surrounding them. We'll delve into different calculation methods, explore real-world examples, and address frequently asked questions. By the end, you'll have a comprehensive understanding of percentages and their practical implications.
Calculating 5% of 500,000: The Methods
There are several ways to calculate 5% of 500,000. Let's explore the most common methods:
Method 1: Direct Calculation using Decimal Conversion
The most straightforward method involves converting the percentage to a decimal and multiplying it by the total value. Remember that 5% is equivalent to 5/100 or 0.05.
Therefore:
5% of 500,000 = 0.05 * 500,000 = 25,000
This is the most efficient method for simple percentage calculations.
Method 2: Fraction Method
This method utilizes the fractional representation of the percentage. 5% can be expressed as 5/100. The calculation becomes:
(5/100) * 500,000 = 25,000
This method is helpful for visualizing the proportion and can be particularly useful when dealing with more complex fractions.
Method 3: Breaking Down the Calculation
We can simplify the calculation by finding 1% first and then multiplying by 5.
1% of 500,000 = 500,000 / 100 = 5,000
5% of 500,000 = 5,000 * 5 = 25,000
This method is beneficial for mental calculations or situations where you need to understand the incremental contribution of each percentage point.
Understanding Percentages: Beyond the Calculation
Percentages are a fundamental concept in mathematics and are used extensively across various disciplines. They represent a proportion or fraction of a whole, expressed as a number out of 100. Understanding percentages is crucial for:
-
Financial Literacy: Interest rates, discounts, taxes, investment returns, and inflation are all expressed as percentages. Calculating these accurately is essential for making informed financial decisions. For example, understanding a 5% interest rate on a loan directly impacts the total amount you repay. Understanding a 5% discount on a 500,000 item means saving 25,000.
-
Data Analysis and Statistics: Percentages are used to represent proportions within datasets, facilitating the comparison of different groups or trends. For instance, if 5% of a population has a specific characteristic, this percentage allows for easy understanding and comparison with other populations or subgroups.
-
Scientific Research: In scientific research, percentages are utilized to express experimental results, statistical significance, and error margins. A 5% margin of error in a scientific study, for example, indicates the potential range of variability in the findings.
-
Business and Economics: Businesses rely heavily on percentages for profit margins, sales growth, market share analysis, and cost calculations. Understanding a 5% increase in sales compared to the previous year provides valuable insights into business performance.
Real-World Applications of Percentage Calculations
The calculation of 5% of 500,000, while seemingly simple, has numerous real-world applications:
-
Commission Calculations: Sales representatives often earn a commission based on a percentage of their sales. If a salesperson sells 500,000 worth of goods and earns a 5% commission, their earnings would be 25,000.
-
Tax Calculations: Sales tax, income tax, and other taxes are often calculated as a percentage of a total amount. Understanding how to calculate these percentages is crucial for budgeting and financial planning.
-
Discount Calculations: Retailers frequently offer discounts as percentages. A 5% discount on a 500,000 item results in a savings of 25,000.
-
Investment Growth: Investment returns are often expressed as percentages. If an investment grows by 5% annually, its growth can be directly calculated using the percentage method.
-
Population Statistics: Demographics often involve percentage calculations to understand the distribution of various characteristics within a population. For instance, the percentage of a population that falls within a specific age group or holds a specific occupation is a useful statistic.
Common Misconceptions about Percentages
Despite their seemingly simple nature, several common misconceptions surround percentages:
-
Adding Percentages Directly: A common mistake is adding percentages directly without considering their base values. For example, a 10% increase followed by a 10% decrease does not result in the original value. The final value would be slightly lower.
-
Confusing Percentage Change with Absolute Change: It's crucial to differentiate between the percentage change and the absolute change in a value. A 5% increase on a small base value represents a smaller absolute change compared to a 5% increase on a large base value.
-
Incorrect Interpretation of Percentage Points: A change from 10% to 15% is a 5 percentage point increase, not a 50% increase. This distinction is important for clear communication and accurate analysis.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage increase or decrease?
To calculate a percentage increase, find the difference between the new and old values, divide by the old value, and multiply by 100. For a decrease, the process is similar, but the result will be negative.
Q2: What are percentage points?
Percentage points refer to the absolute difference between two percentages. For instance, an increase from 20% to 25% is a 5 percentage point increase.
Q3: How can I improve my understanding of percentages?
Practice regularly with various problems, focusing on different methods of calculation and real-world applications. Utilize online resources and educational materials to strengthen your understanding.
Q4: Are there any online tools to help with percentage calculations?
Yes, many online calculators and tools are available to assist with percentage calculations. However, understanding the underlying principles remains crucial for effective usage and problem-solving.
Conclusion: The Power of Percentages
Calculating 5% of 500,000 – while a seemingly basic arithmetic problem – serves as a gateway to understanding the broader significance of percentages in our daily lives. From financial decisions to scientific research, percentages provide a concise and easily understandable way to represent proportions and analyze data. By mastering the principles of percentage calculations and avoiding common misconceptions, you'll enhance your analytical skills and navigate the world of numbers with greater confidence. Remember that the true power of understanding percentages lies not just in the ability to perform calculations, but in the ability to interpret and apply those calculations to make informed decisions in diverse contexts. The seemingly simple calculation of 25,000 from 5% of 500,000 unlocks a world of understanding across many disciplines.
Latest Posts
Latest Posts
-
20 Degrees C In F
Sep 13, 2025
-
Is Ethanol Heavier Than Water
Sep 13, 2025
-
1 Kilo Ohm To Ohm
Sep 13, 2025
-
Daffodils Poem By William Wordsworth
Sep 13, 2025
-
Tales Of The Dying Earth
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent Of 500 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.