8 Divided By 1 6
catronauts
Sep 14, 2025 · 5 min read
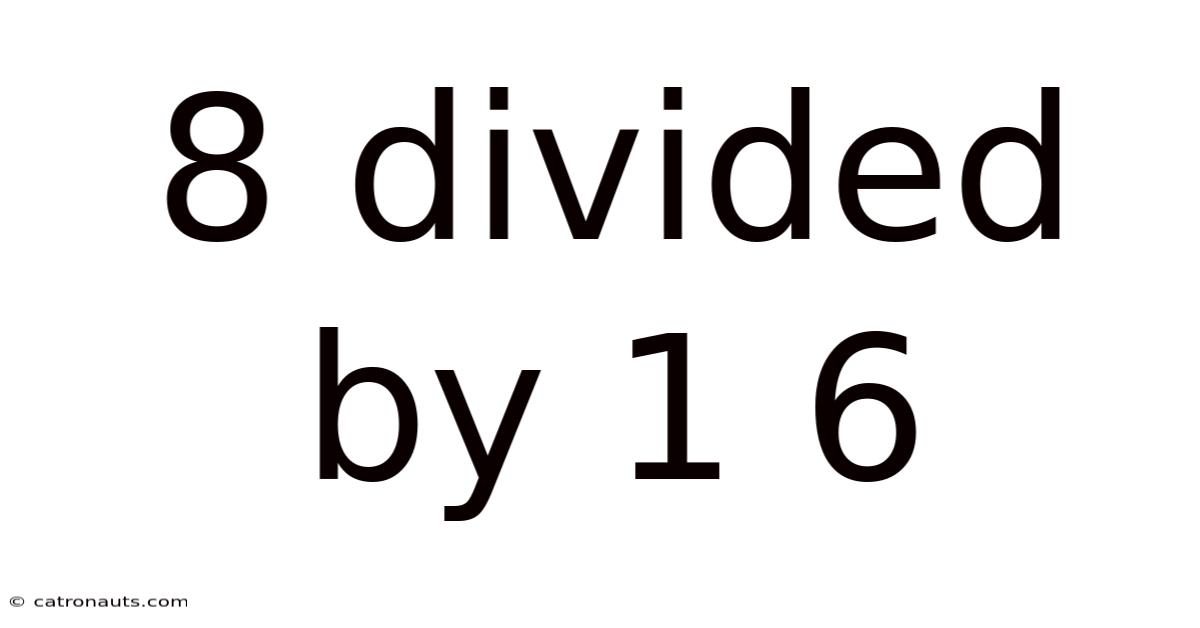
Table of Contents
Decoding 8 Divided by 1/6: A Deep Dive into Fraction Division
Understanding how to divide by fractions is a cornerstone of mathematical proficiency. This seemingly simple operation – 8 divided by 1/6 – often trips up students, but with a clear understanding of the principles involved, it becomes straightforward. This article will not only solve 8 ÷ 1/6 but also explore the underlying concepts, providing a solid foundation for tackling similar problems and building confidence in fraction manipulation. We will cover various methods, delve into the mathematical rationale, and address frequently asked questions to ensure a comprehensive understanding.
Understanding Fraction Division: The "Keep, Change, Flip" Method
Before we tackle 8 ÷ 1/6, let's establish a strong understanding of fraction division. The most common method is often remembered by the mnemonic "Keep, Change, Flip" (or KCF). This refers to the following steps:
- Keep: Keep the first number (the dividend) as it is.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (the divisor) – this means inverting the fraction, swapping the numerator and denominator.
Let's illustrate this with a simpler example: 2 ÷ 1/3.
- Keep: Keep the 2.
- Change: Change ÷ to ×.
- Flip: Flip 1/3 to become 3/1 (or simply 3).
So, 2 ÷ 1/3 becomes 2 × 3 = 6.
Solving 8 Divided by 1/6 Using the KCF Method
Now, let's apply the KCF method to solve our main problem: 8 ÷ 1/6.
- Keep: Keep the 8.
- Change: Change ÷ to ×.
- Flip: Flip 1/6 to become 6/1 (or simply 6).
Therefore, 8 ÷ 1/6 becomes 8 × 6 = 48.
The answer to 8 divided by 1/6 is 48.
Beyond the Algorithm: Understanding the Rationale
While the KCF method provides a quick and efficient way to solve fraction division problems, it's crucial to understand the underlying mathematical principles. Division can be interpreted as asking, "How many times does the divisor fit into the dividend?"
In the case of 8 ÷ 1/6, we're asking, "How many times does 1/6 fit into 8?"
To visualize this, imagine you have 8 whole pies. Each pie is cut into 6 equal slices (representing 1/6). The total number of slices is 8 × 6 = 48. Therefore, there are 48 slices of 1/6 in 8 whole pies. This visual representation reinforces the answer we obtained using the KCF method.
Working with Mixed Numbers and Improper Fractions
The KCF method works equally well with mixed numbers and improper fractions. A mixed number combines a whole number and a fraction (e.g., 2 1/2), while an improper fraction has a numerator larger than or equal to its denominator (e.g., 5/2).
Let's consider an example involving a mixed number: 2 1/2 ÷ 1/4.
First, convert the mixed number 2 1/2 into an improper fraction: (2 × 2 + 1)/2 = 5/2.
Now, apply the KCF method:
- Keep: Keep 5/2.
- Change: Change ÷ to ×.
- Flip: Flip 1/4 to become 4/1 (or 4).
So, 5/2 ÷ 1/4 becomes (5/2) × 4 = 20/2 = 10.
The answer is 10.
Reciprocal and its Role in Fraction Division
The "flip" step in the KCF method involves finding the reciprocal of the divisor. The reciprocal of a number is simply 1 divided by that number. For a fraction, the reciprocal is found by switching the numerator and denominator. For example, the reciprocal of 1/6 is 6/1 (or 6), and the reciprocal of 3/4 is 4/3.
Multiplying a number by its reciprocal always results in 1. This property is central to understanding why the KCF method works. By flipping the divisor and changing the operation to multiplication, we are essentially multiplying by the reciprocal, which is a fundamental aspect of division.
Practical Applications of Fraction Division
Understanding fraction division is crucial in various real-world scenarios:
- Cooking and Baking: Scaling recipes up or down requires dividing fractional amounts.
- Construction and Engineering: Precise measurements and calculations often involve fractions.
- Sewing and Tailoring: Cutting fabric and adjusting patterns necessitates working with fractions.
- Finance and Budgeting: Dividing resources and managing finances often involves fractional calculations.
Frequently Asked Questions (FAQ)
Q1: Why does the KCF method work?
A1: The KCF method is a shortcut based on the principle that dividing by a fraction is equivalent to multiplying by its reciprocal. This stems from the definition of division and the properties of fractions.
Q2: Can I divide fractions using a different method?
A2: Yes. You can also divide fractions by converting them to equivalent fractions with a common denominator and then dividing the numerators. However, the KCF method is generally more efficient.
Q3: What if the dividend is a fraction and the divisor is a whole number?
A3: Treat the whole number as a fraction with a denominator of 1. Then apply the KCF method. For example, 1/2 ÷ 2 = 1/2 ÷ 2/1 = 1/2 × 1/2 = 1/4.
Q4: What if I have a complex fraction (a fraction within a fraction)?
A4: Treat the main fraction bar as a division sign and apply the KCF method. For example, (1/2)/(1/4) = 1/2 ÷ 1/4 = 1/2 × 4/1 = 4/2 = 2.
Q5: How can I improve my understanding of fraction division?
A5: Practice is key! Work through numerous examples, using both the KCF method and visualizing the process to reinforce your understanding. Use online resources, textbooks, or work with a tutor if you need additional support.
Conclusion: Mastering Fraction Division
Mastering fraction division is a vital skill that extends far beyond the classroom. By understanding the underlying principles behind the KCF method and practicing regularly, you can develop confidence and proficiency in handling fraction division problems. Remember the simple yet powerful steps: Keep, Change, Flip! This will not only help you solve problems efficiently but also build a stronger foundation in mathematical reasoning. The ability to easily manipulate fractions is a critical component of success in more advanced mathematical concepts and a wide range of real-world applications. So, keep practicing, and you will soon find yourself effortlessly navigating the world of fractions.
Latest Posts
Latest Posts
-
1920s Style Dresses Plus Size
Sep 14, 2025
-
If Roses Grew In Heaven
Sep 14, 2025
-
What Is Leading Digit Approximation
Sep 14, 2025
-
Definition Of Reliability In Science
Sep 14, 2025
-
Meaning Of The Song Demons
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 8 Divided By 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.