Equivalent Fraction Of 7 3
catronauts
Sep 19, 2025 · 6 min read
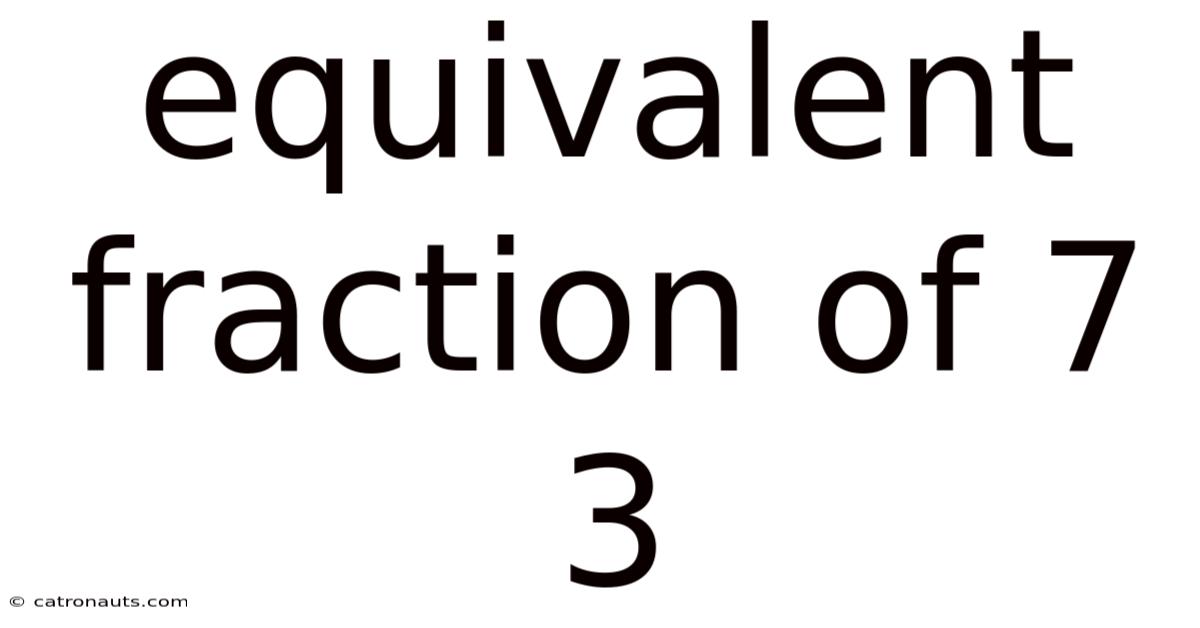
Table of Contents
Understanding Equivalent Fractions: A Deep Dive into 7/3
Equivalent fractions represent the same portion of a whole, even though they look different. This concept is fundamental in mathematics and forms the basis for many advanced operations. This article will explore the concept of equivalent fractions, focusing on the fraction 7/3 and demonstrating how to find and understand its equivalents. We'll delve into the underlying principles, provide practical examples, and answer frequently asked questions, ensuring a thorough understanding for learners of all levels.
Introduction to Equivalent Fractions
An equivalent fraction is simply a fraction that represents the same value as another fraction. Imagine slicing a pizza: one half (1/2) is the same as two quarters (2/4), or four eighths (4/8). All these fractions represent the same amount of pizza. The key to understanding equivalent fractions lies in the principle of multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number. This process maintains the ratio between the numerator and denominator, thus preserving the fraction's value.
Let's illustrate this with a simple example: Consider the fraction 1/2. If we multiply both the numerator and the denominator by 2, we get 2/4. If we multiply by 3, we get 3/6. Both 2/4 and 3/6 are equivalent to 1/2. Similarly, if we divide both the numerator and the denominator of 6/8 by 2, we obtain 3/4, which is an equivalent fraction.
Finding Equivalent Fractions of 7/3
The fraction 7/3 is an improper fraction because the numerator (7) is larger than the denominator (3). This indicates that the fraction represents a value greater than 1. To find equivalent fractions of 7/3, we follow the same principle as before: multiply or divide both the numerator and the denominator by the same non-zero number.
Let's find some equivalent fractions:
- Multiplying by 2: (7 x 2) / (3 x 2) = 14/6
- Multiplying by 3: (7 x 3) / (3 x 3) = 21/9
- Multiplying by 4: (7 x 4) / (3 x 4) = 28/12
- Multiplying by 5: (7 x 5) / (3 x 5) = 35/15
And so on. We can generate an infinite number of equivalent fractions for 7/3 by multiplying both the numerator and denominator by any non-zero integer.
It's important to note that we cannot divide to obtain an equivalent fraction that is simpler than 7/3, as 7 and 3 share no common factors other than 1 (they are relatively prime or coprime). This means 7/3 is already in its simplest form.
Visual Representation of Equivalent Fractions
Visual aids can greatly enhance the understanding of equivalent fractions. Imagine a rectangle divided into three equal parts. If we shade seven of these parts (because we have 7/3), we have more than one whole rectangle shaded.
Now, imagine dividing each of the original three parts into two equal parts. This results in six equal parts in total. We'll now have 14 of these smaller parts shaded (14/6), which is equivalent to the original 7/3. This visual demonstration shows that 7/3 and 14/6 represent the same amount of the rectangle. The same principle can be applied to other equivalent fractions, demonstrating the visual equivalence.
Converting Improper Fractions to Mixed Numbers
The fraction 7/3 is an improper fraction. It's often more convenient to represent improper fractions as mixed numbers. A mixed number consists of a whole number and a proper fraction (where the numerator is smaller than the denominator).
To convert 7/3 to a mixed number, we perform division:
7 ÷ 3 = 2 with a remainder of 1.
This means that 7/3 is equivalent to 2 and 1/3 (written as 2 1/3). This signifies two whole units and one-third of a unit. This representation is often more intuitive and easier to visualize. All equivalent fractions of 7/3 will also convert to the same mixed number, 2 1/3. For example, 14/6 simplifies to 2 2/6, which further simplifies to 2 1/3.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is crucial for various mathematical operations:
- Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. Finding equivalent fractions with a common denominator is essential for this process.
- Comparing Fractions: Determining which of two fractions is larger or smaller often involves finding equivalent fractions with a common denominator.
- Simplifying Fractions: While 7/3 is already simplified, many other fractions need simplification to their lowest terms. This involves finding equivalent fractions with the smallest possible numerator and denominator.
- Ratio and Proportion: Equivalent fractions are the foundation of understanding ratios and proportions. They are used extensively in solving problems involving scale, percentages, and rates.
Further Exploration: Decimal Equivalents
Fractions can also be expressed as decimals. To find the decimal equivalent of 7/3, we perform the division:
7 ÷ 3 ≈ 2.333...
The decimal representation is a repeating decimal, indicated by the ellipsis (...). This signifies that the digit 3 repeats infinitely. Understanding the decimal equivalent helps in comparing fractions to decimal numbers and in using calculators effectively for calculations involving fractions.
Frequently Asked Questions (FAQ)
Q1: How many equivalent fractions does 7/3 have?
A1: There are infinitely many equivalent fractions for 7/3. You can generate them by multiplying both the numerator and denominator by any non-zero integer.
Q2: Is 7/3 in its simplest form?
A2: Yes, 7/3 is in its simplest form because 7 and 3 have no common factors other than 1.
Q3: What is the mixed number equivalent of 7/3?
A3: The mixed number equivalent of 7/3 is 2 1/3.
Q4: How do I find a common denominator for fractions involving 7/3?
A4: To find a common denominator, identify the least common multiple (LCM) of the denominators involved. For instance, if you're adding 7/3 and 1/2, the LCM of 3 and 2 is 6. You would then find equivalent fractions of 7/3 and 1/2 with a denominator of 6.
Q5: Why is understanding equivalent fractions important?
A5: Understanding equivalent fractions is fundamental to many mathematical operations, including adding, subtracting, comparing, and simplifying fractions, as well as working with ratios, proportions, and percentages.
Conclusion
Understanding equivalent fractions is a cornerstone of mathematical literacy. This article has explored the concept in detail, using 7/3 as a central example. We have demonstrated how to find equivalent fractions, visually represent them, convert improper fractions to mixed numbers, and highlighted their practical applications. By mastering the principles discussed here, learners can build a solid foundation for tackling more complex mathematical problems and concepts in the future. Remember, the key is understanding the underlying principle of maintaining the ratio between the numerator and the denominator. Through consistent practice and visualization, the concept of equivalent fractions will become intuitive and readily applicable.
Latest Posts
Latest Posts
-
80 Degrees F To Celsius
Sep 19, 2025
-
Sentences With The Word Though
Sep 19, 2025
-
Bohr Rutherford Diagram Of Magnesium
Sep 19, 2025
-
Amazon Forest In World Map
Sep 19, 2025
-
Ode To Grecian Urn Analysis
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Equivalent Fraction Of 7 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.