Graph Of X 1 X
catronauts
Sep 14, 2025 · 6 min read
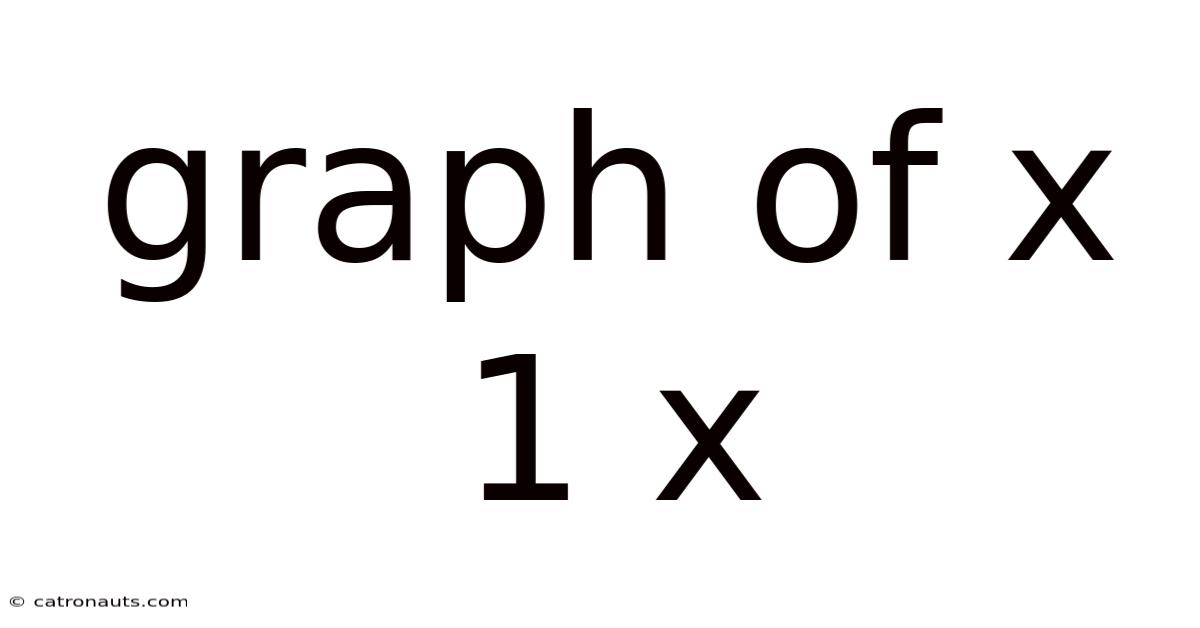
Table of Contents
Unveiling the Mysteries of the Graph of y = 1/x: A Comprehensive Exploration
The graph of y = 1/x, also known as a reciprocal function or a hyperbola, is a fascinating object of study in mathematics. Understanding its characteristics is crucial for grasping concepts in algebra, calculus, and even more advanced fields. This comprehensive guide will delve into the intricacies of this graph, covering its properties, asymptotes, transformations, and practical applications. We'll explore its behavior, dissect its key features, and equip you with the tools to confidently analyze and interpret it.
Introduction: A First Glimpse at y = 1/x
At its core, the equation y = 1/x represents a relationship where y is inversely proportional to x. This means that as x increases, y decreases, and vice-versa. This inverse relationship is what gives the graph its distinctive shape. Understanding this fundamental relationship is the first step towards understanding the graph's more complex features. We'll explore how this simple equation generates a graph with unique characteristics, including its asymptotes and its behavior in different quadrants. We’ll also look at how transformations of this basic function change its position and orientation on the coordinate plane.
Key Features of the Graph: Asymptotes and Branches
The graph of y = 1/x is characterized by two key features: its asymptotes and its two distinct branches.
-
Asymptotes: The graph approaches but never touches the x-axis (y = 0) and the y-axis (x = 0). These lines are called asymptotes. The x-axis is a horizontal asymptote, and the y-axis is a vertical asymptote. Understanding asymptotes is critical to graphing the function accurately. They represent values that x or y can get arbitrarily close to, but never actually reach.
-
Branches: The graph consists of two distinct branches, one in the first quadrant (where both x and y are positive) and one in the third quadrant (where both x and y are negative). These branches are mirror images of each other reflected across the origin (0,0). The symmetry about the origin is another important characteristic of this function.
Constructing the Graph: A Step-by-Step Approach
While plotting numerous points can help generate the graph, understanding the asymptotes and the inverse relationship between x and y provides a more efficient approach.
-
Identify Asymptotes: Begin by drawing the x-axis and y-axis. These will serve as the asymptotes for the function. Remember that the graph will never cross these lines.
-
Plot Key Points: Select a few strategic x-values and calculate the corresponding y-values. For example:
- If x = 1, y = 1/1 = 1
- If x = 2, y = 1/2 = 0.5
- If x = -1, y = 1/-1 = -1
- If x = -2, y = 1/-2 = -0.5
- If x = 0.5, y = 1/0.5 = 2
- If x = -0.5, y = 1/-0.5 = -2
-
Sketch the Branches: Plot the points you calculated. You'll notice that the points in the first quadrant form a curve that approaches the asymptotes. Similarly, the points in the third quadrant form another curve approaching the asymptotes. Connect these points smoothly, remembering that the graph never touches the axes.
Understanding the Behavior of the Function: Increasing and Decreasing Intervals
The function y = 1/x is a decreasing function in both its branches. This means that as x increases, y decreases, and vice-versa. This characteristic is crucial for understanding its behavior and applications in various fields like optimization problems. The function is always decreasing on the intervals (-∞, 0) and (0, ∞).
Transformations of the Basic Function: Shifts, Stretches, and Reflections
The basic function y = 1/x can be transformed by applying various operations to it. These transformations alter the position, size, and orientation of the graph.
-
Vertical Shift: Adding a constant 'k' to the function (y = 1/x + k) shifts the graph vertically upwards if k is positive and downwards if k is negative. The horizontal asymptote will shift accordingly.
-
Horizontal Shift: Replacing x with (x - h) in the function (y = 1/(x - h)) shifts the graph horizontally to the right if h is positive and to the left if h is negative. The vertical asymptote will shift accordingly.
-
Vertical Stretch/Compression: Multiplying the function by a constant 'a' (y = a/x) stretches the graph vertically if |a| > 1 and compresses it if 0 < |a| < 1.
-
Horizontal Stretch/Compression: Replacing x with bx (y = 1/(bx)) compresses the graph horizontally if |b| > 1 and stretches it if 0 < |b| < 1.
-
Reflection: Negating the function (y = -1/x) reflects the graph across the x-axis, while negating x (y = 1/(-x)) reflects it across the y-axis.
The Derivative and the Second Derivative: A Calculus Perspective
Applying calculus techniques provides a deeper understanding of the function's behavior.
-
First Derivative: The derivative of y = 1/x is dy/dx = -1/x². This derivative is always negative for x ≠ 0, confirming that the function is always decreasing in its defined intervals.
-
Second Derivative: The second derivative is d²y/dx² = 2/x³. This is positive for x > 0 (concave up) and negative for x < 0 (concave down). This explains the concavity of the branches.
Applications of y = 1/x: Real-World Connections
The reciprocal function finds applications in various real-world scenarios:
-
Physics: Inverse relationships are common in physics. For example, the relationship between force and distance in an inverse square law (like gravity) can be modeled using a similar function.
-
Economics: The relationship between supply and demand can sometimes be modeled using reciprocal functions, showing how price changes affect quantity demanded or supplied.
-
Engineering: In certain engineering problems, reciprocal functions might model the relationship between variables, such as the relationship between speed and time required to cover a fixed distance.
-
Computer Science: In algorithms and data structures, inverse relationships can occur in the analysis of time and space complexity.
Frequently Asked Questions (FAQ)
-
Q: Is the function y = 1/x continuous? A: No, it's discontinuous at x = 0 because the function is undefined at this point.
-
Q: Does the function have any x-intercepts or y-intercepts? A: No, it does not have any intercepts because it never crosses either axis.
-
Q: What is the domain and range of the function? A: The domain is all real numbers except 0, and the range is also all real numbers except 0. We can write this as: Domain: (-∞, 0) U (0, ∞) and Range: (-∞, 0) U (0, ∞)
-
Q: How does the graph change if we add a constant to the numerator (y = (1+k)/x)? A: Adding a constant to the numerator changes the y-values proportionally, effectively stretching or compressing the graph vertically.
-
Q: How can I use transformations to graph y = 2/(x-3) + 1? A: This graph is a transformation of y = 1/x. It's stretched vertically by a factor of 2, shifted 3 units to the right, and 1 unit upwards.
Conclusion: A Deeper Understanding of y = 1/x
The graph of y = 1/x, although seemingly simple, reveals a wealth of mathematical concepts. By understanding its asymptotes, branches, behavior, transformations, and applications, we gain a deeper appreciation for the beauty and power of mathematical functions. This comprehensive exploration has equipped you with the knowledge to confidently analyze and interpret this fundamental function and its variations. Remember that continued practice and exploration will further solidify your understanding. The journey into the world of mathematical functions is a rewarding one, and this function serves as an excellent starting point for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Net For A Pentagonal Pyramid
Sep 14, 2025
-
A Thousand Splendid Suns Book
Sep 14, 2025
-
Example Of A Thematic Analysis
Sep 14, 2025
-
How Do You Measure Salinity
Sep 14, 2025
-
What Is A Labour Resource
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Graph Of X 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.