Half Of 2 1 2
catronauts
Sep 16, 2025 · 6 min read
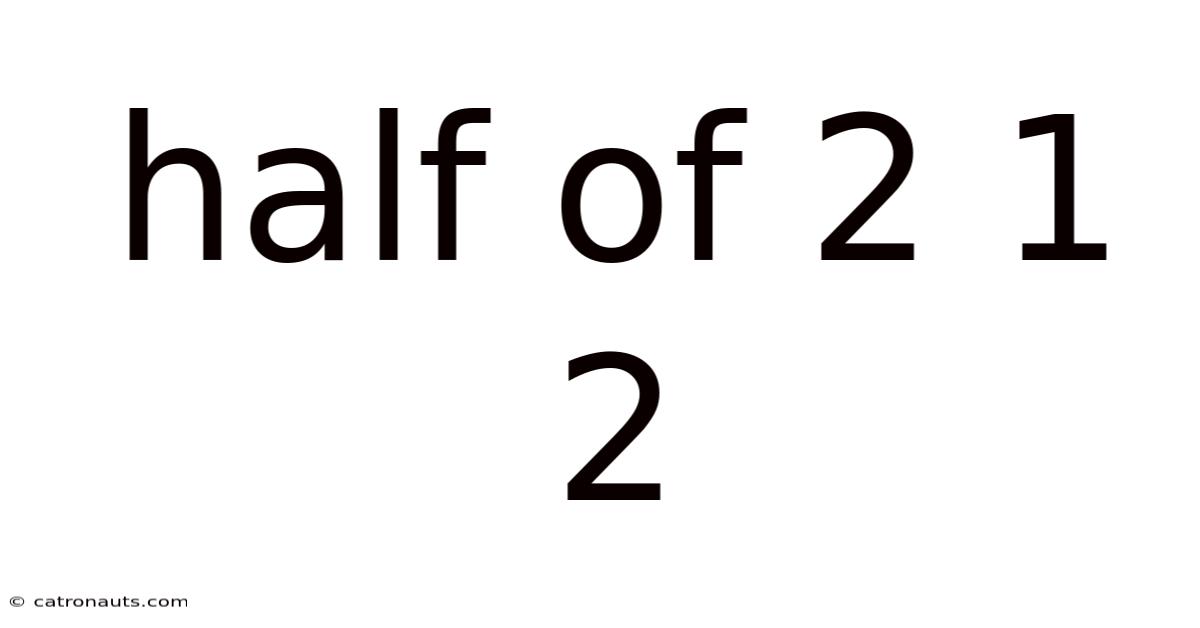
Table of Contents
Decoding "Half of 2 1 2": Exploring Mathematical Ambiguity and Problem-Solving Strategies
The seemingly simple phrase "half of 2 1 2" presents a fascinating challenge, highlighting the importance of precise mathematical notation and the various strategies we can employ to interpret and solve ambiguous problems. This seemingly straightforward question can actually lead to multiple interpretations and solutions, depending on how we understand the arrangement of numbers and the intended operation. This article will delve into the different possible interpretations, explain the underlying mathematical principles, and provide a structured approach to solving similar ambiguous problems. We'll explore the concepts of order of operations, fractions, and different ways to represent mathematical expressions.
Understanding the Ambiguity
The primary source of ambiguity in "half of 2 1 2" lies in the lack of explicit mathematical symbols. The phrase doesn't clearly define whether "2 1 2" represents a single three-digit number (two hundred and twelve), a concatenation of three separate numbers, or something else entirely. This ambiguity necessitates exploring multiple interpretations.
Interpretation 1: "Half of 212"
This is arguably the most straightforward interpretation. If we assume "2 1 2" represents the number two hundred and twelve, the problem becomes: "half of 212". This is a simple division problem:
-
Calculation: 212 / 2 = 106
-
Solution: Half of 212 is 106.
This interpretation assumes a tacit understanding that the numbers are concatenated to form a single integer, and the "of" indicates multiplication by 1/2 (or division by 2). It's the most likely interpretation for someone with a basic understanding of arithmetic.
Interpretation 2: "Half of (2 + 1 + 2)"
Another plausible interpretation involves treating "2 1 2" as the sum of three individual numbers: 2, 1, and 2. This approach introduces the concept of order of operations (often remembered by the acronym PEMDAS/BODMAS). In this scenario, the calculation would be:
-
Step 1: Sum the numbers: 2 + 1 + 2 = 5
-
Step 2: Find half of the sum: 5 / 2 = 2.5
-
Solution: Half of (2 + 1 + 2) is 2.5.
This interpretation requires understanding that "of" signifies multiplication and prioritizing addition before multiplication according to the order of operations.
Interpretation 3: "Half of (2 * 1 * 2)"
A less common but still valid interpretation treats "2 1 2" as a product of three numbers. Again, the order of operations comes into play:
-
Step 1: Multiply the numbers: 2 * 1 * 2 = 4
-
Step 2: Find half of the product: 4 / 2 = 2
-
Solution: Half of (2 * 1 * 2) is 2.
This interpretation demonstrates that the same sequence of numbers can yield different results depending on the assumed operation between them.
Interpretation 4: Exploring Other Possibilities
Beyond the three primary interpretations above, we can consider less conventional approaches. For instance, we could explore possibilities involving other mathematical operations such as subtraction, exponentiation, or more complex arrangements. However, without explicit symbols or further context, these interpretations lack the same logical foundation as the interpretations already discussed. It's crucial to remember that for a mathematical problem to be well-defined, there must be clear indication of which operations are to be performed and in what order.
The Importance of Mathematical Notation
This exercise highlights the critical role of precise mathematical notation. Ambiguity in notation can lead to multiple interpretations and different solutions. The use of parentheses, brackets, and explicit mathematical symbols such as "+", "-", "×", and "÷" are crucial for eliminating ambiguity and ensuring clear communication of mathematical ideas.
Problem-Solving Strategies for Ambiguous Problems
When confronted with ambiguous mathematical problems, consider the following strategies:
-
Identify potential interpretations: Systematically list all plausible interpretations of the problem statement. Consider different orders of operations, the meaning of implied operators ("of" in this case), and alternative arrangements of the numbers.
-
Apply the order of operations: If the problem includes multiple operations, apply the order of operations (PEMDAS/BODMAS) to ensure consistency and accuracy. Remember that parentheses/brackets take precedence.
-
Check for contextual clues: If the problem is presented within a larger context (such as a word problem or a specific mathematical exercise), look for clues that may suggest a particular interpretation.
-
Consider alternative notations: Rewrite the problem using clear and unambiguous mathematical symbols. This can help in clarifying the intended calculations.
-
Seek clarification: If the ambiguity remains unresolved, seek clarification from the source of the problem. This ensures that you are working with the intended interpretation.
Applying the Strategies to "Half of 2 1 2"
Let's revisit "half of 2 1 2" using these strategies:
-
Potential Interpretations: We've already identified three major interpretations: half of 212, half of (2 + 1 + 2), and half of (2 * 1 * 2).
-
Order of Operations: The second and third interpretations explicitly demonstrate the importance of order of operations. In the absence of parentheses, there is a potential for differing interpretations and resultant answers.
-
Contextual Clues: Without additional context, we cannot rely on contextual clues to determine a single correct interpretation.
-
Alternative Notation: To avoid ambiguity, we could rewrite the problem using clear notation: (212)/2, (2+1+2)/2, or (212)/2.
-
Seek Clarification: If the intent isn't clear, one would need to ask the person posing the question to clarify their intended meaning.
Frequently Asked Questions (FAQ)
Q: Is there a single "correct" answer to "half of 2 1 2"?
A: No, without clearer notation, there is no single correct answer. The "correctness" depends entirely on the interpretation. Each interpretation, when followed consistently, provides a valid solution.
Q: Why is mathematical notation important?
A: Precise notation avoids ambiguity and ensures that mathematical expressions are interpreted consistently by everyone. It's fundamental for clear communication and accurate calculation.
Q: How can I improve my understanding of order of operations?
A: Practice solving problems that involve multiple operations. Focus on applying PEMDAS/BODMAS correctly and using parentheses to group operations when necessary.
Q: What other types of ambiguous mathematical problems exist?
A: Many problems involving implied operations or unclear notation can lead to ambiguity. For example, problems involving fractions, percentages, and exponents can sometimes be open to different interpretations.
Conclusion
The seemingly simple problem of "half of 2 1 2" reveals the importance of precise mathematical notation and the various strategies required to solve ambiguous problems. While multiple solutions exist depending on the interpretation, understanding the underlying mathematical principles, such as order of operations and the various ways numbers can be combined, allows for a thorough and methodical approach. This exercise serves as a valuable reminder that clear communication and unambiguous notation are essential for effective mathematical problem-solving. The ambiguity inherent in this problem highlights the necessity for critical thinking and the exploration of multiple perspectives when dealing with less clearly defined mathematical expressions. This isn't just about finding an answer; it's about understanding the process and the importance of clarity in mathematical language.
Latest Posts
Latest Posts
-
List Of The Perfect Squares
Sep 16, 2025
-
Wirds That End In F
Sep 16, 2025
-
Place Distribution In Marketing Mix
Sep 16, 2025
-
41 Degrees Celsius To Fahrenheit
Sep 16, 2025
-
Computer Software And Operating System
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.