Integrate Cos X Sin X
catronauts
Sep 19, 2025 · 6 min read
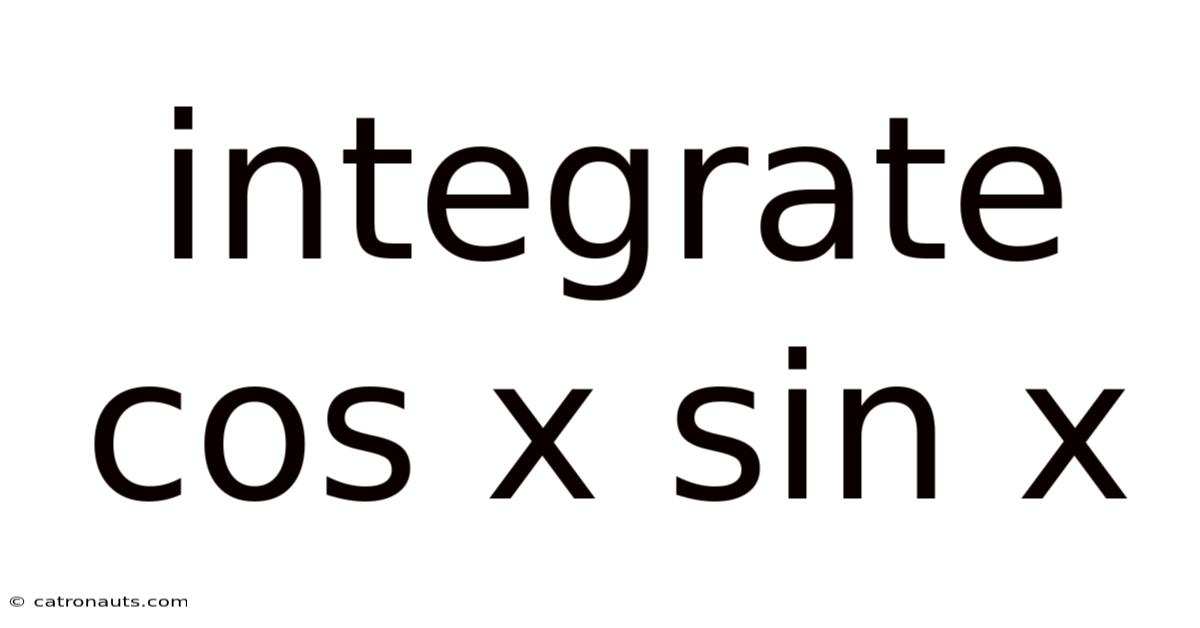
Table of Contents
Integrating cos x sin x: A Comprehensive Guide
Integrating trigonometric functions is a common task in calculus, and integrating the product of cosine and sine, ∫cos x sin x dx, presents a valuable opportunity to explore several integration techniques. This article will guide you through various methods for solving this integral, providing detailed explanations, helpful tips, and addressing frequently asked questions. Understanding this seemingly simple integral unlocks a broader understanding of trigonometric identities and integration strategies.
Introduction: The Power of Trigonometric Identities
The integral ∫cos x sin x dx doesn't immediately lend itself to a straightforward solution. We can't directly apply the basic integration rules. The key to solving this integral lies in employing trigonometric identities to simplify the integrand before integration. We'll explore several approaches, each demonstrating different techniques and highlighting the importance of choosing the right strategy. Mastering these methods will empower you to tackle more complex trigonometric integrals.
Method 1: Using the Double Angle Identity
One of the most efficient ways to integrate cos x sin x is by utilizing the double angle identity for sine: sin 2θ = 2sin θ cos θ. Notice that our integrand, cos x sin x, is half of this identity. Let's see how we can apply this:
-
Rewrite the integrand: We can rewrite cos x sin x as (1/2)sin 2x. This transformation makes the integral significantly easier to solve.
-
Substitute and integrate: Our integral now becomes (1/2)∫sin 2x dx. This is a straightforward integral. Let u = 2x, then du = 2dx, and dx = du/2. Substituting, we have:
(1/2) ∫ sin u (du/2) = (1/4) ∫ sin u du = -(1/4)cos u + C
-
Substitute back: Remember that u = 2x. Substituting back, we get the final answer:
-(1/4)cos 2x + C where C is the constant of integration.
This method leverages a fundamental trigonometric identity to simplify the problem. It's a classic example of how strategic substitution can significantly ease the integration process.
Method 2: Using Integration by Parts
Integration by parts is a powerful technique that allows us to integrate products of functions. The formula for integration by parts is: ∫u dv = uv - ∫v du. Let's apply this to our integral:
-
Choose u and dv: We'll let u = sin x and dv = cos x dx. This choice is somewhat arbitrary; we could have chosen u = cos x and dv = sin x dx, but this choice leads to a simpler solution.
-
Find du and v: Differentiating u, we get du = cos x dx. Integrating dv, we get v = sin x.
-
Apply the integration by parts formula: Substituting into the formula, we get:
∫cos x sin x dx = sin x sin x - ∫sin x cos x dx
Notice that the integral on the right-hand side is the same as the original integral!
-
Solve for the integral: Let I = ∫cos x sin x dx. Then we have:
I = sin²x - I
Adding I to both sides, we get 2I = sin²x. Therefore:
I = (1/2)sin²x + C
-
Alternative form: This result might look different from the result obtained using the double angle formula. However, using the double angle identity cos 2x = 1 - 2sin²x, we can show that they are equivalent:
(1/2)sin²x = (1/2)(1 - cos 2x)/2 = (1/4)(1 - cos 2x) = (1/4) - (1/4)cos 2x
This differs from our previous result by a constant (1/4). Remember that the constant of integration, C, absorbs any constant differences. Thus, both solutions are correct.
Method 3: Using Substitution with a Trigonometric Identity
We can also use substitution along with a different trigonometric identity. Let's use the identity cos²x + sin²x = 1.
-
Rewrite the integrand: Let's rewrite the integral as ∫cos x sin x dx = ∫cos x (sin x) dx
-
Substitution: Let u = sin x. Then du = cos x dx. This substitution directly replaces cos x dx with du.
-
Integrate: The integral transforms to ∫u du = (1/2)u² + C
-
Substitute back: Substituting u = sin x, we get:
(1/2)sin²x + C
This method also yields a result equivalent to those found in the previous methods. Again, the difference in the constant term is absorbed within the constant of integration.
Method 4: Using the Product-to-Sum Formula
The product-to-sum formula provides another approach. This formula states that cos A sin B = (1/2)[sin(A+B) - sin(A-B)]. Applying this to our integral:
-
Apply the Product-to-Sum Formula: With A = x and B = x, we have:
cos x sin x = (1/2)[sin(x+x) - sin(x-x)] = (1/2)[sin 2x - sin 0] = (1/2)sin 2x
-
Integrate: This leads us back to the integral we solved using the double angle formula in Method 1, yielding:
-(1/4)cos 2x + C
This method demonstrates the versatility of trigonometric identities in solving integrals.
A Deeper Dive: The Importance of the Constant of Integration (C)
In each method, we encountered the constant of integration, C. This constant is crucial because the derivative of a constant is zero. Therefore, an indefinite integral always represents a family of functions, all differing by a constant. Failing to include C is a common mistake that can lead to inaccurate results, particularly in applications involving initial conditions or boundary value problems.
Frequently Asked Questions (FAQ)
-
Q: Which method is the best? A: There's no single "best" method. The optimal approach often depends on your familiarity with different techniques and the context of the problem. The double angle identity method is often the quickest and most straightforward for this specific integral.
-
Q: What if the integral were ∫cos 2x sin x dx? A: This requires a different approach. You might need to use the double angle formula for cosine (cos 2x = 1 - 2sin²x or cos 2x = 2cos²x - 1) or employ integration by parts more strategically.
-
Q: Are there other trigonometric integrals similar to this one? A: Yes! Integrals involving products of sine and cosine with different arguments (e.g., ∫cos 3x sin 2x dx) or higher powers of sine and cosine are common in calculus. Mastering these fundamental techniques will equip you to handle more complex scenarios.
-
Q: How can I practice more? A: Work through numerous practice problems in your textbook or online resources. Start with simpler examples and gradually increase the difficulty. Focus on understanding the underlying concepts and choosing the most appropriate method for each integral.
Conclusion: Mastering Trigonometric Integration
Integrating cos x sin x demonstrates the importance of understanding trigonometric identities and choosing the appropriate integration technique. While the double angle identity method offers a direct and efficient solution, integration by parts and the product-to-sum formula provide valuable alternative approaches. Remember to always include the constant of integration, and practice applying these techniques to various problems to solidify your understanding. Proficiency in trigonometric integration is a cornerstone of success in calculus and beyond, laying a strong foundation for tackling more challenging mathematical concepts. The seemingly simple integral ∫cos x sin x dx serves as a gateway to a deeper appreciation of the elegance and power of calculus.
Latest Posts
Latest Posts
-
43 60 As A Percentage
Sep 19, 2025
-
What Are Deeds Of Trust
Sep 19, 2025
-
What Is A Code Brown
Sep 19, 2025
-
Limiting Sum Of Gp Formula
Sep 19, 2025
-
W I T Margaret Edson
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Integrate Cos X Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.