Is 2/3 Bigger Than 3/4
catronauts
Sep 17, 2025 · 5 min read
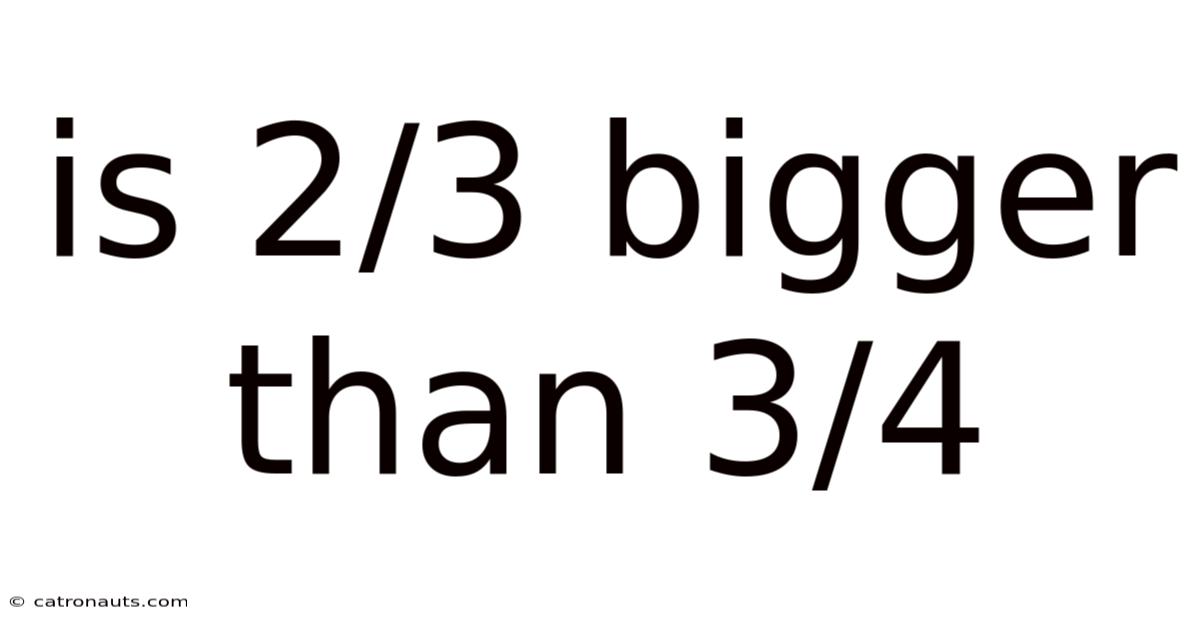
Table of Contents
Is 2/3 Bigger Than 3/4? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for various aspects of life, from cooking and construction to finance and advanced scientific calculations. This article will delve into the seemingly simple question: Is 2/3 bigger than 3/4? We'll not only answer this directly but also explore several methods for comparing fractions, equipping you with the tools to confidently tackle similar problems in the future. This will include a detailed explanation of different approaches, addressing common misconceptions and solidifying your understanding of fractional concepts.
Understanding Fractions: A Quick Refresher
Before we jump into comparing 2/3 and 3/4, let's quickly review the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts we're considering.
For example, in the fraction 2/3, the denominator (3) tells us the whole is divided into three equal parts, and the numerator (2) tells us we're considering two of those parts.
Method 1: Finding a Common Denominator
This is arguably the most straightforward method for comparing fractions. The core principle is to rewrite both fractions so they share the same denominator. Once they have the same denominator, we can directly compare their numerators. The fraction with the larger numerator is the larger fraction.
To find a common denominator for 2/3 and 3/4, we need to find a number that is divisible by both 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
-
Converting 2/3: To change the denominator from 3 to 12, we multiply both the numerator and denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
Converting 3/4: To change the denominator from 4 to 12, we multiply both the numerator and denominator by 3: (3 x 3) / (4 x 3) = 9/12
Now we can compare 8/12 and 9/12. Since 9 > 8, we conclude that 9/12 (which is equivalent to 3/4) is larger than 8/12 (which is equivalent to 2/3).
Therefore, 3/4 is bigger than 2/3.
Method 2: Converting to Decimals
Another effective way to compare fractions is to convert them into decimals. This involves dividing the numerator by the denominator for each fraction.
-
Converting 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667 (This is a repeating decimal)
-
Converting 3/4 to a decimal: 3 ÷ 4 = 0.75
Comparing the decimal values, we see that 0.75 > 0.6667.
Therefore, 3/4 is bigger than 2/3.
Method 3: Visual Representation
While not as precise as the previous methods for complex fractions, visualizing fractions can be incredibly helpful for building intuitive understanding, especially for beginners. Imagine two identical pies.
-
2/3: Cut one pie into three equal slices and take two of them.
-
3/4: Cut the other pie into four equal slices and take three of them.
By visually comparing the amount of pie in each case, it becomes clear that the three-quarters slice (3/4) is larger than the two-thirds slice (2/3). This visual approach helps solidify the conceptual understanding of fraction comparison.
Method 4: Cross-Multiplication
This method provides a quick and efficient way to compare fractions without finding a common denominator. Cross-multiply the numerators and denominators of the two fractions.
-
Cross-multiply 2/3 and 3/4:
(2 x 4) = 8 (3 x 3) = 9
Since 9 > 8, the fraction with the larger product (3/4) is the larger fraction.
Therefore, 3/4 is bigger than 2/3.
Why Understanding Fraction Comparison Matters
The ability to compare fractions is essential for various mathematical operations and real-world applications. Here are a few examples:
-
Solving equations: Many algebraic equations involve fractions, and comparing them is crucial for finding solutions.
-
Data analysis: In statistics and data analysis, comparing fractions (e.g., percentages or proportions) is fundamental for interpreting data and drawing conclusions.
-
Measurement and scaling: In construction, cooking, and other fields, accurately comparing fractions of measurements is essential for precision and accuracy.
-
Financial calculations: Fractions are frequently used in finance, including calculating interest rates, loan repayments, and profit margins.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to compare fractions?
A: Yes, you can use a calculator to convert fractions to decimals and then compare them. However, understanding the underlying methods for comparing fractions is crucial for developing strong mathematical skills.
Q: What if the fractions have different denominators and numerators?
A: Regardless of the numbers, you can always employ the methods described above (finding a common denominator, converting to decimals, or cross-multiplication) to compare fractions effectively.
Q: Are there any other methods for comparing fractions?
A: While the methods described above are the most common and efficient, other advanced techniques exist, such as using the concept of least common denominators and simplifying fractions before comparison.
Q: What happens if the fractions are equal?
A: If, after using any of the methods, the results are equal, then the fractions are equivalent. For instance, 1/2 and 2/4 are equivalent fractions.
Conclusion
Determining whether 2/3 is bigger than 3/4 involves understanding the fundamental concepts of fractions and applying appropriate comparison techniques. Through the methods of finding a common denominator, converting to decimals, visual representation, and cross-multiplication, we've clearly established that 3/4 is indeed larger than 2/3. Mastering these methods not only provides a definitive answer to this specific question but also equips you with the skills to confidently compare any two fractions, regardless of their complexity. This understanding forms the bedrock for further advancements in mathematics and numerous practical applications across diverse fields. Remember to practice these methods regularly to build your confidence and proficiency in working with fractions.
Latest Posts
Latest Posts
-
Lens Length Of Human Eye
Sep 17, 2025
-
46 60 As A Percentage
Sep 17, 2025
-
Lever Types In Human Body
Sep 17, 2025
-
Artists Who Use Oil Pastels
Sep 17, 2025
-
Jurassic Park Novel Nedry Death
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Bigger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.