Lcm Of 12 And 8
catronauts
Sep 16, 2025 · 6 min read
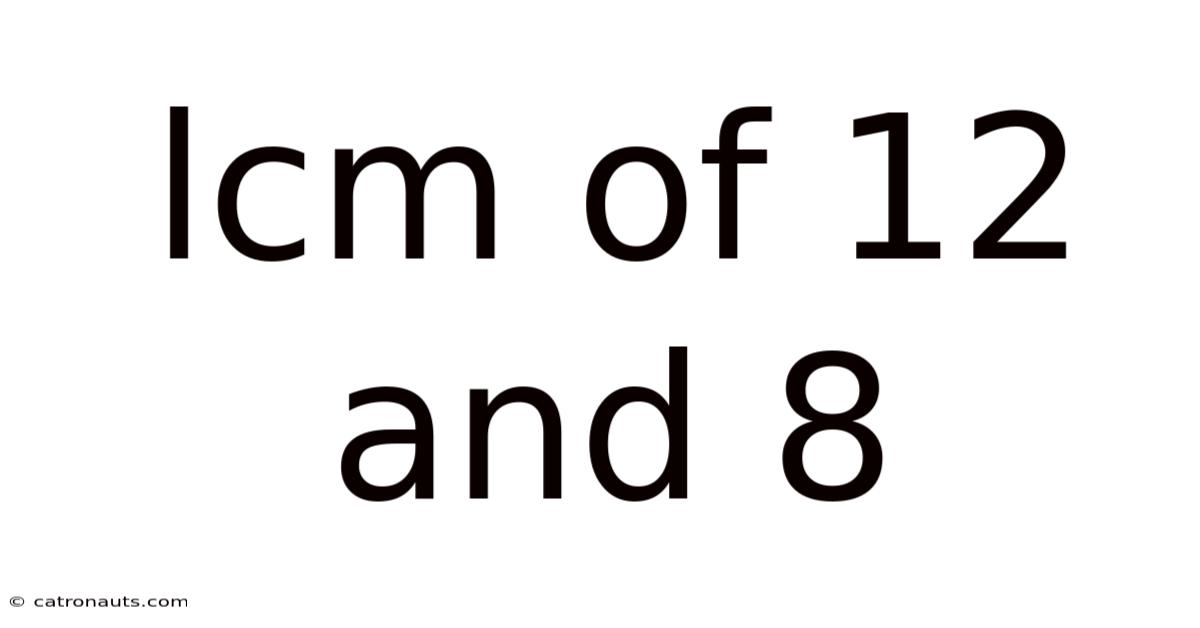
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 8: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for a solid grasp of number theory and its applications in various fields. This article will explore the LCM of 12 and 8 in detail, explaining multiple approaches, delving into the mathematical reasoning behind them, and showcasing their practical relevance. We'll also address frequently asked questions and provide further insights into the broader concept of LCM.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. Understanding LCM is fundamental in various mathematical operations, including simplifying fractions, solving problems involving fractions, and working with rhythmic patterns in music. Let's focus on finding the LCM of 12 and 8.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple that is common to both.
- Multiples of 12: 12, 24, 36, 48, 60, 72, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, ...
By comparing the lists, we observe that the smallest number appearing in both lists is 24. Therefore, the LCM of 12 and 8 is 24. This method works well for small numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the mathematical principles involved. It relies on expressing each number as a product of its prime factors.
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM, we take the highest power of each prime factor present in the factorizations of both numbers:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
Multiplying these highest powers together gives us the LCM: 8 x 3 = 24. Therefore, the LCM of 12 and 8 is 24. This method is particularly useful for larger numbers because it avoids the need to list out all the multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest positive integer that divides both numbers without leaving a remainder. We can use the following formula to find the LCM using the GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two numbers, and GCD(a, b) represents the greatest common divisor of 'a' and 'b'.
Let's find the GCD of 12 and 8 using the Euclidean algorithm:
- Divide the larger number (12) by the smaller number (8): 12 ÷ 8 = 1 with a remainder of 4.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (4): 8 ÷ 4 = 2 with a remainder of 0.
- The last non-zero remainder is the GCD, which is 4.
Now, let's use the formula:
LCM(12, 8) = (|12 x 8|) / GCD(12, 8) = (96) / 4 = 24
Therefore, the LCM of 12 and 8 is 24. This method is efficient for larger numbers as it avoids listing multiples and relies on a well-established algorithm for finding the GCD.
Visual Representation: Venn Diagram
A Venn diagram can provide a visual understanding of the relationship between the LCM and GCD. Representing the prime factorization of each number in separate circles, the overlapping section represents the GCD, while the entire area combined represents the LCM. For 12 (2² x 3) and 8 (2³), the overlapping section (GCD) would be 2², and the total area (LCM) would be 2³ x 3.
Applications of LCM
The LCM has numerous practical applications:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling Problems: Determining when events with different recurring cycles will occur simultaneously (e.g., two buses arriving at the same stop).
- Cyclic Processes: In physics and engineering, understanding repeating cycles often involves using LCM.
- Music Theory: Determining the least common multiple of note durations helps in understanding rhythmic patterns and compositions.
- Computer Science: LCM finds applications in algorithm design and optimization, especially in situations dealing with cycles or repetitions.
Why is Understanding LCM Important?
Beyond the immediate applications mentioned above, understanding LCM cultivates critical mathematical thinking. It strengthens your ability to analyze numbers, identify patterns, and apply different problem-solving techniques. This foundational knowledge is essential for more advanced mathematical concepts and problem-solving skills. Mastering LCM lays the groundwork for understanding more complex topics in algebra, number theory, and beyond.
Frequently Asked Questions (FAQ)
Q: What if the numbers have no common factors?
A: If the two numbers are relatively prime (meaning their GCD is 1), then their LCM is simply the product of the two numbers. For example, the LCM of 9 and 10 (which are relatively prime) is 9 x 10 = 90.
Q: Can we find the LCM of more than two numbers?
A: Yes, the concept of LCM extends to more than two numbers. You can use prime factorization or iterative application of the pairwise LCM method to find the LCM of multiple integers. For example, to find the LCM of 12, 8, and 6:
- Find the LCM of 12 and 8 (which is 24).
- Find the LCM of 24 and 6 (which is 24).
Therefore, the LCM of 12, 8, and 6 is 24.
Q: Is there a shortcut for finding the LCM of large numbers?
A: While prime factorization remains efficient, for extremely large numbers, more advanced algorithms exist, but they often require specialized software or programming. The fundamental principles, however, remain the same.
Q: How does LCM relate to GCD?
A: The LCM and GCD are inversely proportional. As the GCD increases, the LCM decreases, and vice-versa. Their relationship is formalized in the formula: LCM(a, b) x GCD(a, b) = |a x b|.
Conclusion
Finding the least common multiple of 12 and 8, while seemingly a simple task, provides a gateway to understanding a fundamental concept in number theory. We explored three different methods: listing multiples, prime factorization, and using the GCD. Each method offers a unique perspective and level of efficiency, underscoring the importance of versatility in mathematical problem-solving. Understanding LCM is not only valuable for solving specific mathematical problems but also cultivates a deeper understanding of number relationships and mathematical thinking, proving essential for future mathematical endeavors. Remember, the key is to choose the method best suited to the numbers involved, and to understand the underlying principles that connect these methods. Practice and exploration will solidify your understanding and ability to tackle even more complex LCM problems.
Latest Posts
Latest Posts
-
Art Elements And Principles Vce
Sep 16, 2025
-
Grief The Thing With Feathers
Sep 16, 2025
-
Whats Half Of A Liter
Sep 16, 2025
-
The Rainbow Snake Dreamtime Story
Sep 16, 2025
-
Algebraic Fractions Adding And Subtracting
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.