Square Root Of 2 500
catronauts
Sep 11, 2025 · 5 min read
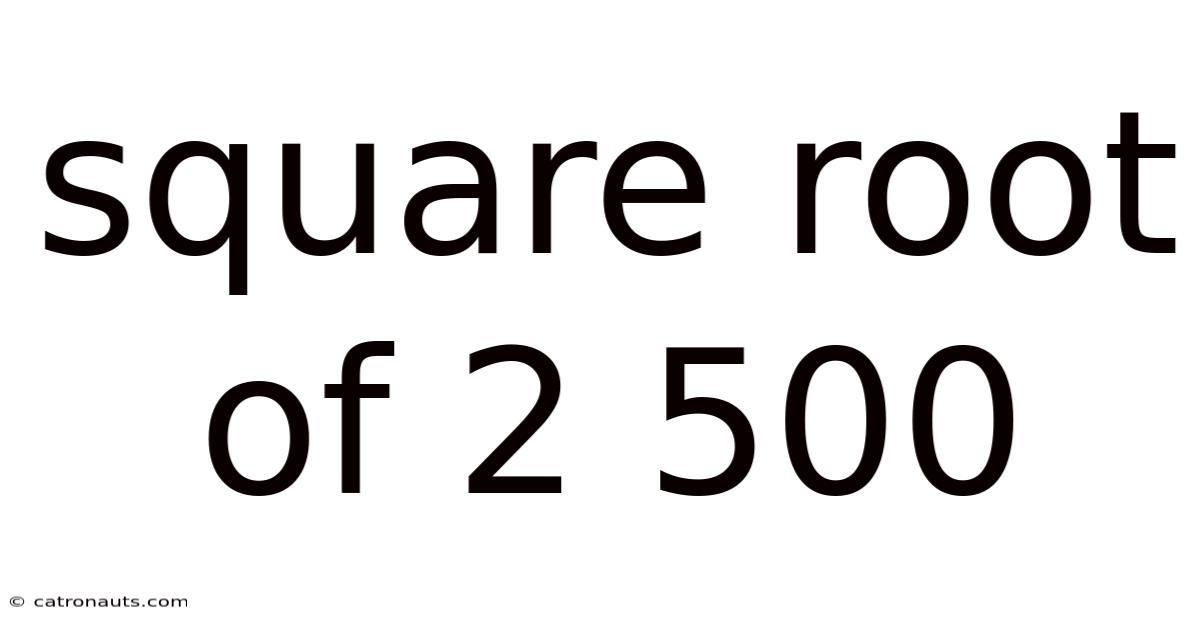
Table of Contents
Unveiling the Mysteries of the Square Root of 2500: A Deep Dive
Finding the square root of a number might seem like a simple mathematical operation, particularly with a seemingly straightforward number like 2500. However, understanding the concept behind square roots, exploring different methods of calculation, and appreciating the broader mathematical context can reveal surprising depth and elegance. This article will delve into the square root of 2500, exploring its calculation, its implications in various fields, and addressing common questions surrounding square roots. We will move beyond a simple answer and unravel the fascinating world of numbers and their relationships.
Understanding Square Roots: A Foundation
Before we tackle the square root of 2500, let's establish a solid understanding of what a square root actually is. In essence, the square root of a number is a value that, when multiplied by itself (squared), results in the original number. For example, the square root of 9 is 3 because 3 * 3 = 9. This seemingly simple concept has profound implications in various areas of mathematics and beyond.
The square root is often represented by the symbol √. Therefore, the square root of 2500 can be written as √2500. Finding this square root means finding the number that, when multiplied by itself, equals 2500.
Calculating the Square Root of 2500: Multiple Approaches
There are several ways to calculate the square root of 2500. Let's explore a few:
1. Prime Factorization:
This method is particularly useful for larger numbers and provides a deeper understanding of the number's composition. We break down 2500 into its prime factors:
- 2500 = 25 * 100
- 25 = 5 * 5
- 100 = 10 * 10 = 2 * 5 * 2 * 5
Therefore, the prime factorization of 2500 is 2² * 5⁴. To find the square root, we take half the exponent of each prime factor:
- √2500 = √(2² * 5⁴) = 2¹ * 5² = 2 * 25 = 50
Thus, the square root of 2500 is 50.
2. Using a Calculator:
The simplest and most efficient method for many, especially with larger numbers, is to use a calculator. Most calculators have a dedicated square root function (√). Simply input 2500 and press the square root button, and you'll instantly get the answer: 50.
3. Estimation and Trial and Error:
For those who prefer a more hands-on approach, estimation and trial and error can be surprisingly effective, especially with numbers that are relatively easy to work with. We know that 50 * 50 = 2500, which makes the square root 50. While this example is straightforward, this method can be less efficient for larger, more complex numbers.
The Significance of Square Roots: Applications in Various Fields
Square roots are not merely abstract mathematical concepts; they have crucial applications across a wide range of fields. Let's look at some examples:
1. Geometry:
Square roots are fundamental to geometry. Calculating the diagonal of a square, the hypotenuse of a right-angled triangle (using the Pythagorean theorem), or the circumference of a circle all involve square roots.
2. Physics:
Many physical phenomena are described by equations that involve square roots. For instance, calculating velocity, acceleration, or energy often requires the use of square roots. The calculation of the escape velocity of a rocket from a planet's gravitational field necessitates the use of square roots.
3. Engineering:
Engineering projects frequently involve calculations that utilize square roots. Structural engineers use square roots when calculating stress, strain, and deflection in various structural components. Civil engineers might employ square roots when calculating the dimensions of roads or bridges. Electrical engineers apply them in circuit calculations.
4. Finance:
Square roots are used in various financial calculations, including determining standard deviation, a measure of the variability of returns in investment portfolios.
5. Computer Science:
Square roots are used in computer graphics and image processing algorithms. They play a key role in various optimization processes.
6. Statistics:
In statistical analysis, the standard deviation, a crucial measure of data dispersion, involves calculating the square root of the variance.
Beyond the Basics: Exploring Irrational and Complex Numbers
While the square root of 2500 is a whole number, not all square roots are so neatly defined. Consider the square root of 2. This is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on infinitely without repeating. Approximations are frequently used for irrational numbers in practical applications.
Moving further into the realm of numbers, we encounter complex numbers. These involve the imaginary unit 'i', where i² = -1. The square root of a negative number results in a complex number. For example, √-1 = i, and √-9 = 3i. While seemingly abstract, complex numbers are vital in various advanced mathematical applications, particularly in electrical engineering and quantum mechanics.
Frequently Asked Questions (FAQ)
Q1: Is there only one square root for a positive number?
A1: While we typically focus on the positive square root (the principal square root), every positive number actually has two square roots: a positive and a negative one. For example, the square roots of 2500 are +50 and -50, because both 50 * 50 = 2500 and -50 * -50 = 2500.
Q2: How can I calculate the square root of a number without a calculator?
A2: For smaller, perfect squares, mental calculation or prime factorization can be used. For larger numbers, iterative methods like the Babylonian method (also known as Heron's method) provide a way to approximate the square root through successive refinements.
Q3: What is the difference between a square root and a square?
A3: Squaring a number means multiplying it by itself (e.g., 5² = 25). Finding the square root is the inverse operation; it's finding the number that, when squared, gives the original number (e.g., √25 = 5).
Q4: Are all square roots rational numbers?
A4: No. Many numbers, like √2, √3, and √5, are irrational numbers, meaning their decimal representation is non-terminating and non-repeating.
Conclusion: A Deeper Appreciation of Square Roots
The seemingly simple operation of finding the square root of 2500 opens a door to a wealth of mathematical concepts and applications. From the elegance of prime factorization to the practical applications in various scientific and engineering fields, the square root reveals the interconnectedness and power of mathematical principles. While a calculator might provide a quick answer, understanding the underlying concepts provides a deeper appreciation for the beauty and utility of mathematics. This exploration goes beyond a simple numerical result; it's a journey into the fascinating world of numbers and their profound influence on our understanding of the world around us.
Latest Posts
Latest Posts
-
Capital Of Finland Crossword Clue
Sep 11, 2025
-
What Is A Persuasive Device
Sep 11, 2025
-
Terminating Decimal And Repeating Decimal
Sep 11, 2025
-
Division And Multiplication Of Decimals
Sep 11, 2025
-
How Do You Write French
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.