The Square Root Of 64
catronauts
Sep 14, 2025 · 7 min read
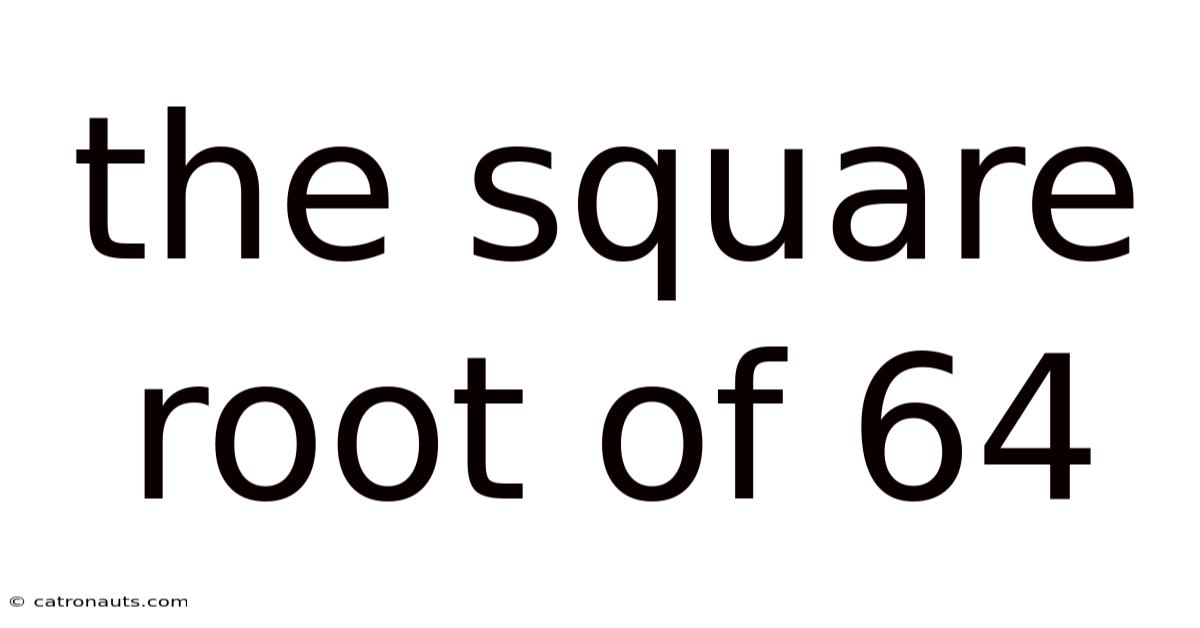
Table of Contents
Delving Deep into the Square Root of 64: More Than Just 8
The square root of 64. A seemingly simple concept, easily calculated by most as 8. But beneath this straightforward answer lies a wealth of mathematical richness, exploring fundamental concepts applicable across numerous fields, from basic arithmetic to advanced calculus. This article will dissect the square root of 64, unraveling its significance and exploring its connections to broader mathematical ideas. We'll go beyond the simple answer and delve into the "why" behind the calculation, exploring its properties and applications.
Introduction: Understanding Square Roots
Before diving into the specifics of the square root of 64, let's establish a solid understanding of what a square root actually is. In essence, the square root of a number is a value that, when multiplied by itself (squared), equals the original number. For instance, the square root of 9 is 3 because 3 multiplied by 3 (3²) equals 9. This can be expressed mathematically as √9 = 3. The symbol '√' denotes the square root operation.
This concept extends to all non-negative real numbers. Every positive real number has two square roots: a positive and a negative one. For example, the square roots of 25 are +5 and -5, because both 5 x 5 = 25 and (-5) x (-5) = 25. However, when we talk about the square root of a number (without specifying positive or negative), we generally refer to the principal square root, which is the non-negative one. Thus, √25 = 5.
Now, let's focus on our target number: 64.
Calculating the Square Root of 64: The Simple Approach
The most straightforward way to find the square root of 64 is to consider which number, when multiplied by itself, results in 64. Through basic multiplication knowledge, or by using a calculator, we quickly arrive at the answer: 8. This is because 8 x 8 = 64. Therefore, √64 = 8.
This simple calculation serves as the foundation for understanding more complex aspects of square roots.
Beyond the Basic: Exploring the Properties of Square Roots
The square root of 64, while seemingly simple, exhibits properties relevant to broader mathematical principles. Let's delve into some of these:
-
Perfect Squares: 64 is a perfect square, meaning it's the result of squaring an integer (8² = 64). Perfect squares are significant because their square roots are whole numbers, unlike numbers like 2 or 7 which are not perfect squares and have irrational square roots.
-
Factorization: The square root operation is intimately connected to prime factorization. 64 can be factored as 2 x 2 x 2 x 2 x 2 x 2, or 2⁶. This factorization allows us to express the square root as √(2⁶) = 2³ = 8. This method is particularly helpful for larger perfect squares, enabling a simpler calculation method.
-
Exponents and Radicals: Square roots are closely tied to exponents. The square root of a number 'x' can be represented as x^(1/2). Therefore, √64 is equivalent to 64^(1/2), which equals 8. This notation extends to other roots such as cube roots (x^(1/3)), fourth roots (x^(1/4)), and so on. This connection highlights the consistent mathematical relationships between exponentiation and radical operations.
-
Geometric Interpretation: The square root of 64 has a clear geometric interpretation. Imagine a square with an area of 64 square units. The length of each side of this square would be the square root of 64, which is 8 units. This visual representation helps solidify the concept of square roots and their link to geometric shapes and areas.
Advanced Concepts: Extending the Understanding
The square root of 64, while seemingly elementary, serves as a stepping stone to more advanced mathematical concepts:
-
Complex Numbers: While we’ve focused on real numbers, the concept of square roots extends to complex numbers. Complex numbers involve the imaginary unit 'i', defined as the square root of -1 (i² = -1). Although 64 doesn't directly involve complex numbers, the principle of extending the square root operation to more abstract number systems is crucial in higher-level mathematics.
-
Calculus: Square roots appear frequently in calculus, particularly in differentiation and integration. Understanding the behavior of square root functions is essential for solving various calculus problems, including optimization problems and finding areas under curves. The derivative and integral of the square root function are important tools in many applied fields, from physics and engineering to economics.
-
Numerical Methods: For numbers that aren't perfect squares, finding their square roots might require numerical methods. These methods, such as the Babylonian method (also known as Heron's method), utilize iterative calculations to approximate the square root to a desired level of accuracy. Understanding these methods deepens the understanding of computational mathematics.
Practical Applications: Where the Square Root of 64 is Used
The square root, in its various applications, is prevalent across numerous fields. While the square root of 64 itself might not directly feature in many everyday calculations, the underlying concept of square roots is crucial in several areas:
-
Geometry and Engineering: Calculating areas, volumes, and distances often involves square roots. Engineers and architects utilize this regularly in design and construction projects.
-
Physics: In physics, the concept of square roots is crucial in calculating velocity, acceleration, and other kinematic quantities. Many physical equations involve square roots, emphasizing the fundamental role of square roots in various physical phenomena.
-
Computer Science: Computer algorithms frequently utilize square root calculations for tasks like image processing, game development, and data analysis. Efficient square root algorithms are essential for optimizing the performance of various software applications.
-
Statistics: Square roots are used in calculating standard deviation and other statistical measures which are essential for data analysis and interpretation. This application is critical in understanding the spread and variability within a dataset.
Frequently Asked Questions (FAQ)
-
What is the opposite of a square root? The opposite of a square root is squaring (raising to the power of 2). If you take the square root of a number and then square the result, you get back the original number (unless you're dealing with negative numbers and only considering the principle square root).
-
Can you find the square root of a negative number? Within the realm of real numbers, you cannot find the square root of a negative number. This is because no real number, when multiplied by itself, results in a negative value. However, this leads to the concept of complex numbers, where the imaginary unit 'i' is introduced to represent the square root of -1.
-
How can I calculate the square root of a large number without a calculator? For large numbers that aren't perfect squares, approximate methods like the Babylonian method or logarithmic tables can be used. These methods involve iterative calculations to achieve an approximate answer. Modern calculators and computer software make this process significantly easier and more accurate.
-
Is there more than one square root for a given positive number? Yes, every positive real number has two square roots – a positive and a negative one. However, when referring to "the" square root, we generally mean the positive (principal) square root.
Conclusion: The Profound Simplicity of √64
While the square root of 64 might seem like a trivial calculation – simply 8 – its significance extends far beyond this straightforward answer. It serves as a gateway to understanding fundamental mathematical concepts like perfect squares, prime factorization, exponents, radicals, and even complex numbers. Its application across various fields, from basic geometry to advanced calculus and computer science, highlights its importance in both theoretical and practical contexts. Understanding the square root of 64 is not just about the answer; it's about grasping the underlying mathematical principles and appreciating their far-reaching implications. This seemingly simple number holds a surprisingly profound mathematical depth, showcasing the beauty and interconnectedness of mathematical ideas.
Latest Posts
Latest Posts
-
Rightward Shift In Demand Curve
Sep 15, 2025
-
Catholic Adam And Eve Story
Sep 15, 2025
-
What Is Anionic And Cationic
Sep 15, 2025
-
Legal Consent Age In Mississippi
Sep 15, 2025
-
Was Muscovy A Mongol Subject
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about The Square Root Of 64 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.