What 15 Percent Of 200
catronauts
Sep 11, 2025 · 6 min read
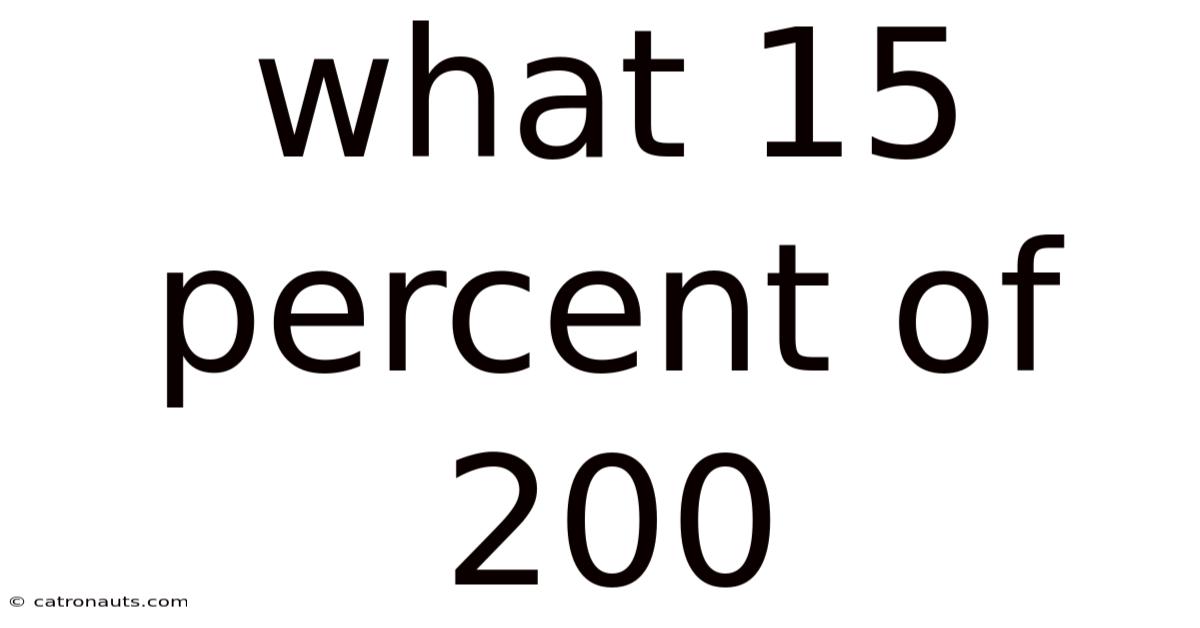
Table of Contents
What is 15 Percent of 200? A Deep Dive into Percentages and Their Applications
Finding 15 percent of 200 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying principles of percentages and their diverse applications is crucial for navigating various aspects of life, from everyday finances to complex scientific calculations. This article will not only provide the answer to "What is 15 percent of 200?" but also delve deeper into the concept of percentages, explore different methods of calculation, and showcase their relevance in real-world scenarios.
Understanding Percentages: A Foundational Concept
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" ("per centum" in Latin). It's a way of representing a portion of a whole. For example, 50% means 50 out of 100, or one-half. Percentages are incredibly versatile tools used to express proportions, rates of change, discounts, interest rates, and much more. Mastering percentage calculations is essential for effective financial management, data analysis, and problem-solving in numerous fields.
Calculating 15 Percent of 200: Three Different Approaches
There are several ways to calculate 15% of 200. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage into its decimal equivalent by dividing it by 100. 15% becomes 0.15 (15 ÷ 100 = 0.15). Then, we multiply this decimal by the number we want to find the percentage of:
200 x 0.15 = 30
Therefore, 15% of 200 is 30.
Method 2: Using Fractions
Percentages can also be represented as fractions. 15% can be written as 15/100. To find 15% of 200, we multiply the fraction by 200:
(15/100) x 200 = 30
This method simplifies the calculation by canceling out common factors. Notice that 100 divides into 200 twice, simplifying the equation to:
15 x 2 = 30
Method 3: Using Proportion
This method is particularly useful for understanding the relationship between the percentage, the whole, and the part. We can set up a proportion:
15/100 = x/200
Here, 'x' represents the unknown value (15% of 200). To solve for 'x', we cross-multiply:
100x = 15 x 200
100x = 3000
x = 3000/100
x = 30
This approach reinforces the concept of proportional relationships and provides a more visual understanding of the calculation.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios. Here are a few examples:
-
Financial Literacy: Calculating discounts, sales tax, interest rates, tips, and loan payments all require a firm grasp of percentage calculations. Understanding these concepts empowers you to make informed financial decisions, manage your budget effectively, and avoid overspending. For instance, if a store offers a 20% discount on a $100 item, you can quickly calculate the discount amount ($20) and the final price ($80).
-
Data Analysis and Interpretation: Percentages are widely used to represent data in various contexts, such as market research, scientific studies, and economic indicators. For example, understanding the percentage change in a company's revenue over time is crucial for assessing its financial performance. Similarly, understanding demographic percentages (e.g., the percentage of the population in a specific age group) is essential for policymaking and resource allocation.
-
Scientific Calculations and Measurements: Percentages play a vital role in numerous scientific disciplines. For example, in chemistry, concentration is often expressed as a percentage (e.g., percentage by weight or percentage by volume). In biology, percentage change in population size is used to track species growth or decline.
-
Everyday Life: Percentages are embedded in our daily routines. We encounter them when calculating the tip at a restaurant, figuring out the interest earned on a savings account, or determining the percentage of tasks completed on a project. This understanding assists in efficient task management and personal productivity.
Beyond the Basics: More Complex Percentage Problems
While calculating 15% of 200 is relatively simple, more complex percentage problems might require multiple steps. Here are a few examples:
-
Finding the original value: If you know the percentage and the resulting value, you can calculate the original value using reverse percentage calculations. For example, if an item is on sale for $60 after a 25% discount, you can determine the original price by setting up an equation: 0.75x = 60, where x is the original price.
-
Calculating percentage change: This involves comparing two values and determining the percentage increase or decrease. The formula is: [(New Value - Old Value) / Old Value] x 100. For example, if a stock price increased from $50 to $60, the percentage change would be: [(60 - 50) / 50] x 100 = 20%.
-
Compound interest: This involves earning interest on both the principal amount and accumulated interest over time. The formula is more complex and requires repeated calculations for each period.
Frequently Asked Questions (FAQ)
Q: How can I quickly calculate percentages in my head?
A: For simple percentages like 10%, 20%, or 50%, mental estimation is quite easy. For 10%, simply move the decimal point one place to the left. For 20%, double the 10% value. For 50%, divide by two. For other percentages, rounding off to easier values can provide a close approximation.
Q: Are there any online tools or calculators for percentage calculations?
A: Yes, many online calculators are available that can perform various percentage calculations, including finding the percentage of a number, calculating percentage change, and solving more complex percentage problems. However, understanding the underlying principles is more important than relying solely on calculators.
Q: What are the common mistakes people make when working with percentages?
A: Common mistakes include incorrectly converting percentages to decimals, misinterpreting percentage change, and neglecting to consider the impact of compounding when dealing with interest or growth rates.
Q: Why is understanding percentages important in everyday life?
A: Understanding percentages is critical for making informed decisions in various areas of your life, including financial management, shopping, budgeting, investing, and interpreting data in news and media.
Conclusion: Mastering the Power of Percentages
This article has demonstrated that calculating 15% of 200 is straightforward, yielding an answer of 30. However, the true value lies in grasping the broader concepts surrounding percentages and their vast applications. From everyday financial decisions to complex scientific calculations, the ability to work confidently with percentages is a valuable skill that enhances problem-solving abilities and improves decision-making across numerous aspects of life. By understanding the different methods of calculation and their real-world applications, you can harness the power of percentages to navigate the world more effectively. Remember to practice regularly to solidify your understanding and build confidence in tackling more complex percentage problems.
Latest Posts
Latest Posts
-
Life Cycle Of A Crocodile
Sep 11, 2025
-
Example Of A Statute Law
Sep 11, 2025
-
How Old Is Ashley Justice
Sep 11, 2025
-
Florida Age Of Sexual Consent
Sep 11, 2025
-
1 Kg How Many Grams
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What 15 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.