What Is 10 Of 200
catronauts
Sep 10, 2025 · 6 min read
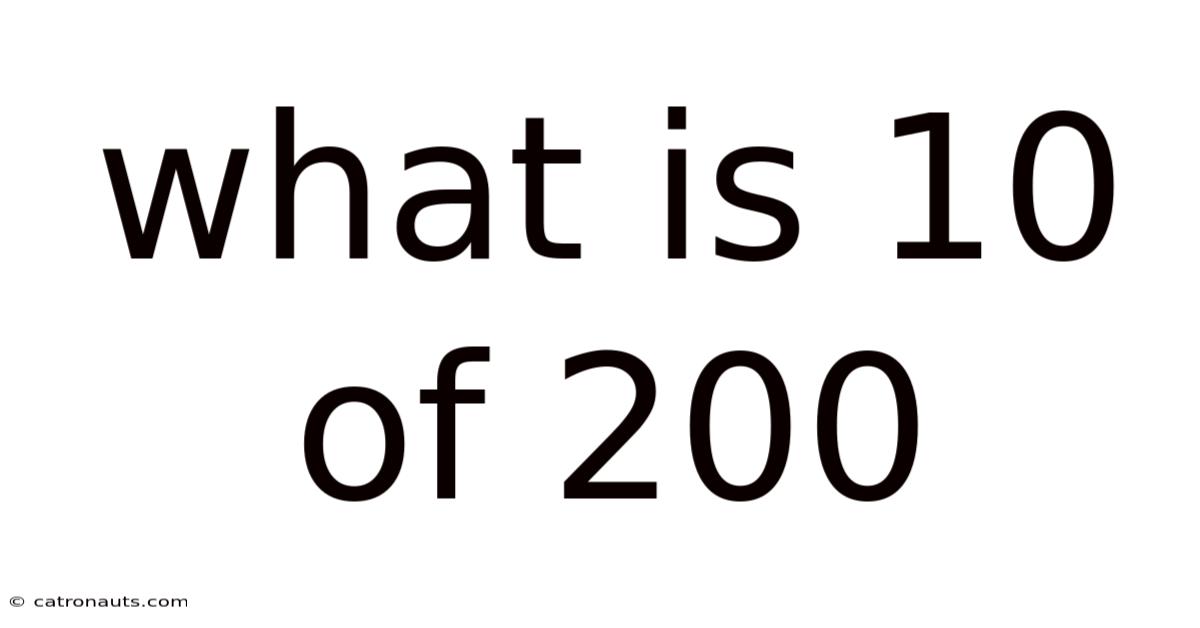
Table of Contents
What is 10% of 200? A Deep Dive into Percentages and Their Applications
Finding 10% of 200 might seem like a simple calculation, a piece of cake for anyone who remembers basic arithmetic. But this seemingly straightforward problem opens a door to a fascinating world of percentages, their applications in everyday life, and even their underlying mathematical principles. This article will not only answer the question "What is 10% of 200?" but also delve into the 'why' and 'how' behind percentage calculations, offering a comprehensive understanding that goes beyond a simple numerical answer.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10% literally means 10 out of every 100. This fundamental concept underpins all percentage calculations. We use percentages extensively because they provide a standardized way to compare proportions and ratios across different datasets. Whether you're calculating discounts at a store, understanding interest rates on a loan, or analyzing statistical data, percentages offer a convenient and universally understood method.
Calculating 10% of 200: Three Methods
There are several ways to calculate 10% of 200. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
Since 10% means 10 out of 100, it can be expressed as the fraction 10/100, which simplifies to 1/10. To find 10% of 200, we simply multiply 200 by 1/10:
200 x (1/10) = 20
Therefore, 10% of 200 is 20.
Method 2: Converting Percentage to Decimal
Another approach involves converting the percentage to its decimal equivalent. To do this, we divide the percentage by 100. 10% divided by 100 is 0.10 or simply 0.1. Then, we multiply this decimal by 200:
200 x 0.1 = 20
This method provides the same result: 10% of 200 is 20.
Method 3: Using Proportions
We can also solve this problem using proportions. We set up a proportion where x represents the unknown value (10% of 200):
10/100 = x/200
To solve for x, we cross-multiply:
10 * 200 = 100 * x
2000 = 100x
x = 2000/100
x = 20
Again, we arrive at the answer: 10% of 200 is 20.
Beyond the Calculation: Understanding the Concept
While the calculation itself is straightforward, understanding the underlying concept is crucial. Imagine you have 200 apples, and you want to give away 10% of them. Using any of the methods above, you'd find that you're giving away 20 apples. This simple example highlights the practical application of percentages in everyday situations.
Applications of Percentages in Real Life
Percentages are ubiquitous in our lives. Here are some examples:
- Retail Discounts: Stores frequently offer discounts expressed as percentages. A "20% off" sale means you pay 80% of the original price.
- Financial Calculations: Interest rates on loans, savings accounts, and credit cards are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
- Taxes: Sales tax, income tax, and other taxes are often calculated as percentages of the taxable amount.
- Statistics and Data Analysis: Percentages are used to represent proportions and trends in data, making it easier to understand complex information. For example, a survey might report that 60% of respondents prefer a particular product.
- Grades and Scores: Academic grades and test scores are often expressed as percentages, representing the proportion of questions answered correctly.
- Scientific Measurements: In various scientific fields, percentages are utilized to represent concentrations, changes, and variations in data.
Dealing with More Complex Percentage Problems
While 10% of 200 is relatively simple, many real-world scenarios involve more complex percentage calculations. Let's consider some examples:
- Finding a percentage of a larger number: What is 15% of 1500? Using the decimal method, we calculate 1500 * 0.15 = 225.
- Calculating the original value after a percentage increase or decrease: An item is on sale for $50 after a 25% discount. What was the original price? Let x be the original price. Then 0.75x = 50, so x = 50/0.75 = $66.67 (approximately).
- Comparing percentages: Which is a better deal: a 15% discount on $100 or a 20% discount on $120? Calculating both, we get $15 and $24 respectively. The second deal is better.
Troubleshooting Common Mistakes
Common mistakes in percentage calculations often stem from misunderstandings of the fundamental concepts. Here are some points to watch out for:
- Confusing percentage increase with percentage points: A 10% increase to 10% is different from an increase of 10 percentage points. The former adds 1% (10% * 0.10 = 1%), resulting in 11%, while the latter adds 10 points directly, resulting in 20%.
- Incorrect decimal conversion: Make sure to always divide the percentage by 100 before multiplying.
- Mixing up the order of operations: Ensure you correctly apply the order of operations (multiplication before addition, etc.).
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate percentages?
A: The easiest method depends on your preference and the complexity of the problem. For simple percentages like 10%, the fraction method is often quickest. For more complex percentages, the decimal method is generally more efficient.
Q: How can I improve my percentage calculation skills?
A: Practice is key! Work through various problems of different complexities. You can find plenty of practice exercises online or in textbooks. Understanding the underlying principles will also greatly improve your accuracy and speed.
Q: Are there any online tools or calculators for percentage calculations?
A: Yes, many online calculators and tools are available that can assist with percentage calculations. However, understanding the underlying principles is vital for problem-solving and for avoiding errors. A calculator should be a tool to verify your work, not a replacement for understanding.
Q: What if the percentage isn't a whole number (e.g., 12.5%)?
A: The process remains the same. Convert the percentage to its decimal equivalent (12.5% = 0.125) and multiply by the number.
Q: How are percentages used in finance?
A: Percentages are fundamental in finance, used for calculating interest rates on loans and investments, determining tax liabilities, and analyzing financial performance. Understanding percentages is essential for making sound financial decisions.
Conclusion
The seemingly simple question, "What is 10% of 200?", unveils a broader understanding of percentages and their significant role in numerous aspects of life. From everyday shopping to complex financial calculations, percentages provide a standardized, efficient, and universally understood language for expressing proportions and ratios. Mastering percentage calculations not only enhances your mathematical skills but also empowers you to make informed decisions in various contexts. Remember to practice regularly, understand the underlying principles, and don't hesitate to use calculators to verify your work. The ability to accurately and confidently work with percentages is a valuable skill that will serve you well in numerous aspects of life.
Latest Posts
Latest Posts
-
1000 Gpm To M3 Hr
Sep 11, 2025
-
Types Of Lines In Art
Sep 11, 2025
-
Definition Of A Tertiary Consumer
Sep 11, 2025
-
145 Degrees Celsius To Fahrenheit
Sep 11, 2025
-
Words That Describe My Mom
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.