What Is 10 Of 250
catronauts
Sep 11, 2025 · 5 min read
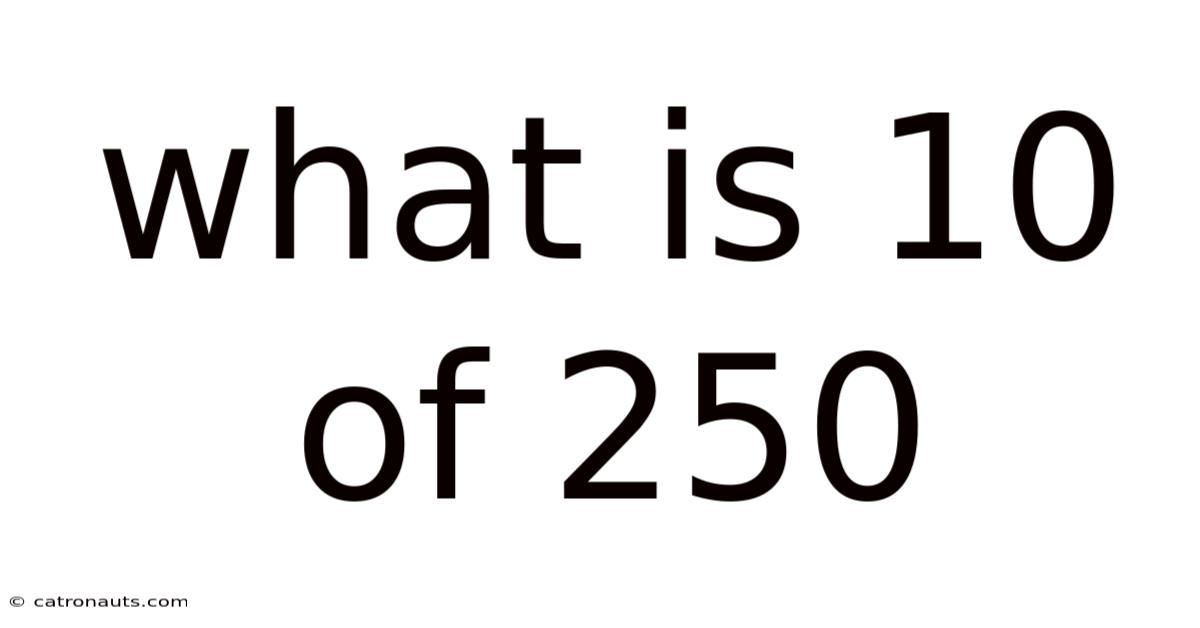
Table of Contents
What is 10% of 250? Understanding Percentages and Their Applications
This article will delve into the seemingly simple question: "What is 10% of 250?" While the answer itself is straightforward, understanding the underlying concepts of percentages and their widespread applications is crucial. We'll explore how to calculate percentages, different methods for solving this specific problem, and then broaden our understanding to show the importance of percentage calculations in various fields. This comprehensive guide will equip you with the knowledge to confidently tackle percentage problems of varying complexity.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 10% means 10 out of 100, or 10/100. This can be simplified to 1/10. Understanding this fundamental concept is key to mastering percentage calculations.
Calculating 10% of 250: Three Methods
There are several ways to calculate 10% of 250. Let's explore three common methods:
Method 1: Using the Fraction Method
As mentioned, 10% is equivalent to 1/10. Therefore, to find 10% of 250, we simply multiply 250 by 1/10:
250 x (1/10) = 25
Therefore, 10% of 250 is 25.
Method 2: Converting Percentage to Decimal
Another common approach involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100. In this case:
10% / 100 = 0.10
Now, multiply this decimal by 250:
250 x 0.10 = 25
Again, we arrive at the answer: 10% of 250 is 25.
Method 3: Using Proportions
This method utilizes the concept of proportions. We can set up a proportion as follows:
10/100 = x/250
Where 'x' represents the value we want to find (10% of 250). To solve for 'x', we cross-multiply:
10 * 250 = 100 * x
2500 = 100x
x = 2500 / 100
x = 25
Once again, we confirm that 10% of 250 is 25.
Beyond the Basics: Understanding Percentage Increase and Decrease
While calculating a simple percentage like 10% of 250 is straightforward, understanding percentage increases and decreases is essential for various real-world applications. Let's consider these scenarios:
-
Percentage Increase: Imagine a product initially priced at 250 is increased by 10%. To calculate the new price, we first find the increase amount (10% of 250 = 25), and then add it to the original price: 250 + 25 = 275. The new price is 275.
-
Percentage Decrease: Conversely, if the price of the 250 product is decreased by 10%, we first find the decrease amount (10% of 250 = 25), and then subtract it from the original price: 250 - 25 = 225. The new price is 225.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in numerous fields, including:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage changes is crucial for analyzing financial statements and making informed investment decisions. For instance, calculating compound interest involves repeated percentage calculations over time.
-
Retail and Sales: Discounts, sales tax, and markups are all expressed as percentages. Retail businesses use percentage calculations to determine pricing strategies, manage inventory, and analyze sales performance. Understanding percentage discounts helps consumers make informed purchasing decisions.
-
Science and Statistics: Percentages are essential for representing data in scientific research and statistical analysis. For example, expressing experimental results as percentages allows for easier comparison and interpretation of data across different studies. This is prevalent in fields such as epidemiology, where infection rates are commonly reported as percentages.
-
Everyday Life: Percentage calculations are part of our daily lives, from calculating tips in restaurants to understanding nutritional information on food labels. Even something as simple as figuring out the percentage of a sale or understanding interest rates on a loan requires understanding percentages.
-
Education: Understanding percentages is fundamental to many subjects, including mathematics, science, and economics. It's a critical skill that underpins more advanced mathematical concepts.
Advanced Percentage Calculations: Finding the Original Value
The previous examples focused on finding a percentage of a given value. However, it's equally important to be able to work backward: finding the original value given a percentage and the resulting value. For instance:
-
Scenario: A product is on sale for 225, representing a 10% discount from the original price. What was the original price?
-
Solution: We can solve this using the following formula:
Original Price = Sale Price / (1 - Discount Rate)
In this case:
Original Price = 225 / (1 - 0.10) = 225 / 0.90 = 250
Therefore, the original price was 250.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage of a number without a calculator?
A1: You can use the fraction method or the decimal method. For example, to calculate 25% of 80, you can convert 25% to 1/4 (25/100 simplified). Then multiply 80 by 1/4, which is 20. Alternatively, convert 25% to 0.25 and multiply by 80, which also gives you 20.
Q2: What if I need to calculate a percentage that's not a whole number, such as 7.5%?
A2: Follow the same principles. Convert 7.5% to its decimal equivalent (0.075) and multiply by the number you're working with.
Q3: Are there any online tools or calculators available to help with percentage calculations?
A3: Yes, numerous online calculators are readily available that can assist with various percentage calculations.
Conclusion
Calculating 10% of 250, while a simple problem, serves as a gateway to understanding the broader world of percentages and their applications. From basic calculations to more complex scenarios involving percentage increases, decreases, and finding original values, the ability to work with percentages is a fundamental skill across many disciplines. Mastering these concepts will enhance your abilities in numerous areas, whether it's managing personal finances, interpreting data, or simply navigating everyday situations that involve percentages. This understanding empowers you to make informed decisions and successfully tackle a wide range of quantitative problems. Remember the core principles – understanding the relationship between fractions, decimals, and percentages is the key to unlocking their potential.
Latest Posts
Latest Posts
-
Why Is Orthodox Easter Different
Sep 11, 2025
-
Melbourne Hosanna Church Of Christ
Sep 11, 2025
-
Define Science As A Product
Sep 11, 2025
-
Differences In Islam And Christianity
Sep 11, 2025
-
Islam Dream Teeth Falling Out
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.