What Is 15 Of 100
catronauts
Sep 13, 2025 · 6 min read
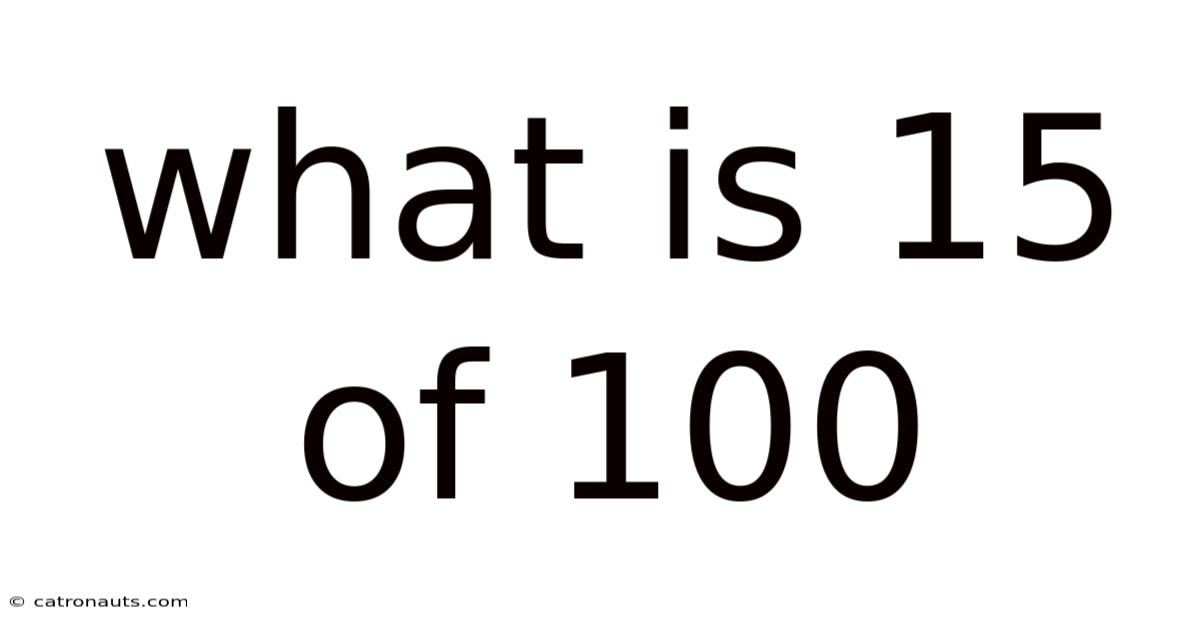
Table of Contents
What is 15 of 100? Deconstructing Percentages and Fractions
What is 15 of 100? This seemingly simple question opens a door to a fundamental concept in mathematics: percentages. Understanding percentages is crucial in various aspects of life, from calculating discounts and interest rates to analyzing data and understanding statistics. This article delves deep into the meaning of "15 of 100," exploring its representation as a fraction, decimal, and percentage, while also offering practical applications and tackling common misconceptions.
Understanding the Fundamentals: Fractions, Decimals, and Percentages
Before we dive into the specifics of 15 out of 100, let's establish a clear understanding of the three core concepts: fractions, decimals, and percentages. These are interconnected and represent different ways of expressing parts of a whole.
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, 1/2 represents one part out of two equal parts.
-
Decimals: Decimals are another way of expressing parts of a whole. They use a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For example, 0.5 is equivalent to 1/2.
-
Percentages: Percentages express a portion of a whole as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100.
15 of 100: The Fraction Representation
"15 of 100" can be directly represented as a fraction: 15/100. This means 15 parts out of a total of 100 equal parts. This fraction is relatively simple and can be easily simplified.
To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. In this case, the GCD of 15 and 100 is 5. Dividing both the numerator and denominator by 5 gives us the simplified fraction: 3/20. This means that 15 out of 100 is the same as 3 out of 20.
15 of 100: The Decimal Representation
Converting a fraction to a decimal involves dividing the numerator by the denominator. So, to find the decimal representation of 15/100, we perform the division: 15 ÷ 100 = 0.15. This decimal reads as "fifteen hundredths." Note that this decimal is directly related to the percentage representation, as explained below.
Alternatively, since we already know that 15/100 simplifies to 3/20, we can also perform the division: 3 ÷ 20 = 0.15. This demonstrates the equivalence between the simplified and unsimplified fractions.
15 of 100: The Percentage Representation
A percentage expresses a fraction as a portion of 100. Since we already have the fraction 15/100, converting it to a percentage is straightforward. We simply multiply the fraction by 100%:
(15/100) * 100% = 15%
Therefore, 15 out of 100 is equivalent to 15 percent. This means that 15 represents 15 parts out of every 100 parts.
Practical Applications of Understanding 15%
Understanding how to represent 15 out of 100 as a fraction, decimal, and percentage has numerous real-world applications. Here are a few examples:
-
Discounts: If a store offers a 15% discount on an item, you know that you will save 15 out of every 100 dollars (or other currency) of the item's original price. For example, a $100 item would have a discount of $15 (15% of $100).
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Understanding percentages allows you to calculate the amount of tax you will owe.
-
Grade Calculations: In many grading systems, your final grade is calculated as a percentage of the total possible points. Understanding percentages helps you track your progress and determine your overall grade.
-
Data Analysis: Percentages are widely used in data analysis to represent proportions and changes over time. They allow for easy comparison and interpretation of data.
Beyond the Basics: Extending the Concept
The understanding of 15/100 extends beyond simply calculating percentages. It forms a basis for more complex calculations involving proportions, ratios, and rates. For example:
-
Finding a percentage of a larger number: If you want to find 15% of 250, you would multiply 250 by 0.15 (the decimal equivalent of 15%). This results in 37.5.
-
Determining the original value: If you know that 15% of a number is 30, you can set up an equation to solve for the original number (x): 0.15x = 30. Solving for x gives you x = 200.
-
Comparing proportions: You can use percentages to compare proportions across different datasets. For example, if one group has 15% of its members participating in an activity and another group has 20%, you can immediately see the difference in participation rates.
Addressing Common Misconceptions
Despite its simplicity, the concept of percentages can sometimes be confusing. Here are a few common misconceptions:
-
Adding percentages directly: You cannot simply add percentages together without considering the base amounts. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Confusing percentage change with absolute change: A 10% increase on a small number represents a smaller absolute change than a 10% increase on a large number.
-
Incorrectly using percentages with different base amounts: Comparing percentages across different base amounts can be misleading if the base amounts are significantly different.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of the fraction 15/100?
A1: The simplest form of 15/100 is 3/20. This is achieved by dividing both the numerator and denominator by their greatest common divisor, which is 5.
Q2: How do I convert a fraction to a percentage?
A2: To convert a fraction to a percentage, multiply the fraction by 100%. For example, 3/20 * 100% = 15%.
Q3: How do I calculate 15% of a number?
A3: To calculate 15% of a number, multiply the number by 0.15 (the decimal equivalent of 15%).
Q4: What is the difference between 15% and 0.15?
A4: 15% and 0.15 are equivalent representations of the same value. 15% is the percentage form, while 0.15 is the decimal form.
Q5: Can I add percentages directly?
A5: No, you generally cannot add percentages directly unless they are based on the same whole. You need to consider the base amounts before adding the resulting values.
Conclusion: Mastering Percentages for Everyday Life
Understanding what 15 of 100 represents—as a fraction (15/100 or 3/20), decimal (0.15), and percentage (15%)—is crucial for navigating various aspects of daily life. This seemingly basic concept forms the foundation for more complex mathematical operations and problem-solving. By mastering the concept of percentages, you equip yourself with a valuable tool for analyzing data, making informed decisions, and confidently handling numerical challenges in various settings. Remember to always focus on the underlying meaning of fractions and proportions to avoid common pitfalls and misconceptions. The ability to confidently work with percentages empowers you to engage more effectively with the quantitative world around you.
Latest Posts
Latest Posts
-
Instruments That Start With A
Sep 13, 2025
-
Country With The Longest Name
Sep 13, 2025
-
Australian And New Zealand Flags
Sep 13, 2025
-
What Is The Number Bond
Sep 13, 2025
-
Venn Diagram Prokaryotic And Eukaryotic
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.