What Is 20 Of 2000.00
catronauts
Sep 15, 2025 · 5 min read
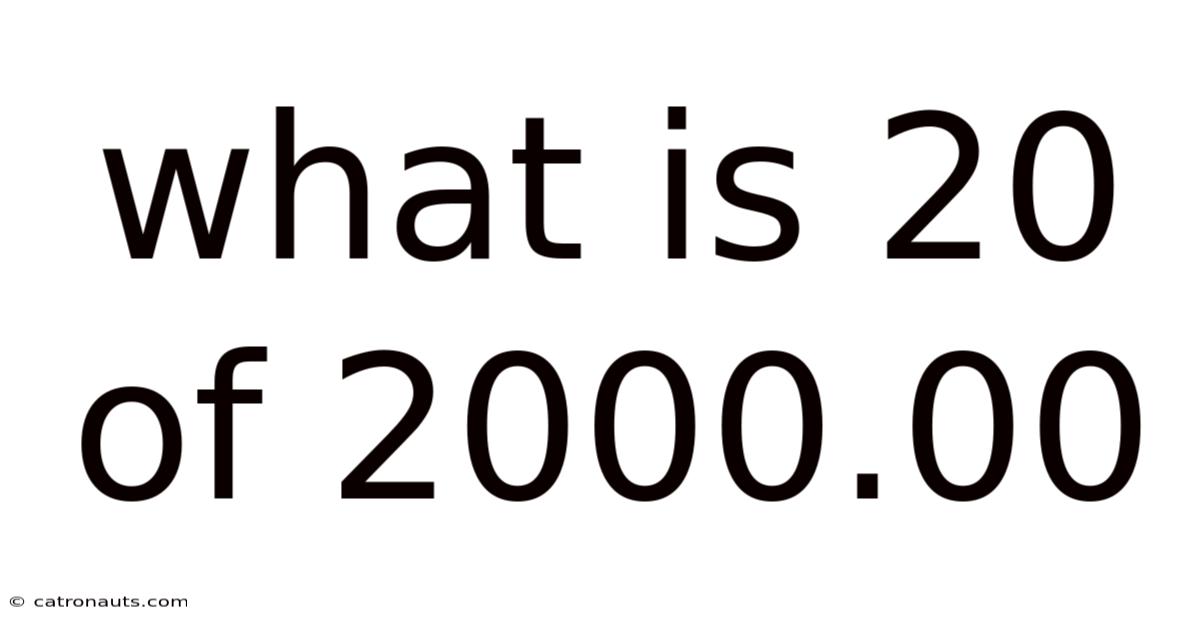
Table of Contents
What is 20 of 2000.00? Understanding Percentages and Proportions
This article explores the seemingly simple question: "What is 20 of 2000.00?" While the calculation itself is straightforward, understanding the underlying concepts of percentages and proportions offers valuable insights into various mathematical applications and real-world scenarios. We will delve into the calculation, explain the methodology, and explore the broader implications of understanding proportional relationships.
Introduction: Percentages and Proportions in Everyday Life
The phrase "20 of 2000.00" inherently involves a proportional relationship. We're essentially asking what proportion 20 represents of the total value 2000.00. Understanding percentages and proportions is crucial in numerous daily situations, from calculating discounts and taxes to analyzing data and understanding financial statements. Whether you're budgeting your monthly expenses, evaluating investment returns, or simply trying to figure out the tip at a restaurant, the ability to quickly and accurately calculate percentages is a valuable skill. This article aims to not only answer the specific question but also provide a solid foundation in these essential mathematical concepts.
Calculating 20 of 2000.00: A Step-by-Step Approach
The most straightforward way to determine "20 of 2000.00" is to calculate the percentage that 20 represents of 2000.00. This involves several steps:
-
Identify the parts: We have two key numbers: 20 (the part) and 2000.00 (the whole).
-
Set up the equation: We can express this relationship as a fraction: 20/2000.00
-
Convert to a decimal: Divide 20 by 2000.00: 20 ÷ 2000.00 = 0.01
-
Convert to a percentage: Multiply the decimal by 100%: 0.01 x 100% = 1%
Therefore, 20 is 1% of 2000.00.
Understanding Percentage Calculations: Different Approaches
While the above method is perfectly adequate, there are alternative approaches to calculating percentages, each offering a slightly different perspective:
-
Using proportions: We can set up a proportion to solve this problem. Let 'x' represent the percentage:
20/2000.00 = x/100
Cross-multiplying, we get:
2000x = 2000
Solving for x:
x = 1
Therefore, x = 1%, confirming our previous result.
-
Using the percentage formula: The basic percentage formula is:
(Part/Whole) x 100% = Percentage
Substituting our values:
(20/2000.00) x 100% = 1%
This formula provides a clear and concise method for solving percentage problems.
Beyond the Calculation: Exploring Proportional Relationships
The concept of proportion extends far beyond simple percentage calculations. Proportional relationships are fundamental to many areas of mathematics and science. Understanding proportions allows us to:
-
Scale quantities: Imagine you need to double a recipe. You'll need to proportionally increase all the ingredients. Similarly, if you're working with maps or blueprints, you need to understand the scale to accurately interpret the measurements.
-
Analyze data: Proportions are essential for analyzing data sets. For instance, if you have data on sales figures, you can calculate the proportion of sales from different regions or product categories.
-
Solve problems involving ratios: Ratios are closely related to proportions. A ratio compares two quantities, while a proportion states that two ratios are equal. Many real-world problems involve solving for an unknown quantity in a ratio or proportion.
Real-World Applications of Percentages and Proportions
The applications of percentages and proportions are vast and varied. Here are a few examples:
-
Finance: Calculating interest rates, loan payments, investment returns, and tax rates all rely heavily on percentage calculations.
-
Business: Analyzing sales data, calculating profit margins, and determining market share all require understanding proportions.
-
Science: Many scientific formulas and calculations involve proportions and ratios. For example, in chemistry, stoichiometry uses proportions to determine the amounts of reactants and products in chemical reactions.
-
Everyday life: Calculating tips, discounts, and sales tax all involve percentage calculations. Understanding proportions helps in scaling recipes, interpreting maps, and even comparing the prices of different products.
Expanding the Understanding: Dealing with Larger and Smaller Numbers
While the example used a relatively simple set of numbers, the principles remain the same even when dealing with much larger or smaller numbers. The key is to always maintain the same logical approach:
-
Large numbers: If you were calculating "20 of 200,000," the process would be identical. You would still divide 20 by 200,000 and then multiply by 100% to find the percentage.
-
Decimal numbers: If the 'whole' number was a decimal, such as "20 of 2000.50," the same procedure applies. Divide 20 by 2000.50 and then multiply by 100%. Calculators are helpful for these types of calculations.
-
Scientific notation: For extremely large or small numbers, scientific notation might be used. The principles of proportion remain unchanged; however, the calculation might require converting the numbers out of scientific notation first.
Frequently Asked Questions (FAQ)
Q1: What if I need to find a percentage of a number greater than 100%?
A1: The same principle applies. For example, to find 150% of 500, you would multiply 500 by 1.5 (which is 150% expressed as a decimal).
Q2: How can I quickly estimate percentages without a calculator?
A2: There are several mental math techniques you can use to estimate percentages. For example, 10% is easy to calculate: just move the decimal point one place to the left. 5% is half of 10%, 25% is one-quarter, etc. Practice helps develop these mental calculation skills.
Q3: Are there any online tools or calculators to help with percentage calculations?
A3: Yes, many online calculators and tools are readily available to help with percentage calculations, providing quick and accurate results.
Q4: What is the difference between a ratio and a proportion?
A4: A ratio is a comparison of two quantities. A proportion is a statement that two ratios are equal.
Conclusion: Mastering Percentages and Proportions
This article has comprehensively addressed the question "What is 20 of 2000.00?", illustrating that it represents 1%. However, its primary aim was not just to provide the answer but to provide a deeper understanding of percentages and proportions, their underlying mathematical principles, and their extensive real-world applications. Mastering these concepts is crucial for success in various academic and professional fields, and a strong grasp of these principles enhances problem-solving skills across numerous contexts. By understanding these fundamental mathematical relationships, we can confidently navigate various challenges and unlock further insights into the world around us. Remember, the more you practice, the more confident and proficient you'll become in tackling percentage and proportion problems.
Latest Posts
Latest Posts
-
What Do Prayer Flags Represent
Sep 15, 2025
-
Crime And Punishment Book Review
Sep 15, 2025
-
23 24 As A Percent
Sep 15, 2025
-
Hardest Substance In Human Body
Sep 15, 2025
-
Types Of Exudate From Wounds
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 2000.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.