What Is 20 Of 40
catronauts
Sep 17, 2025 · 6 min read
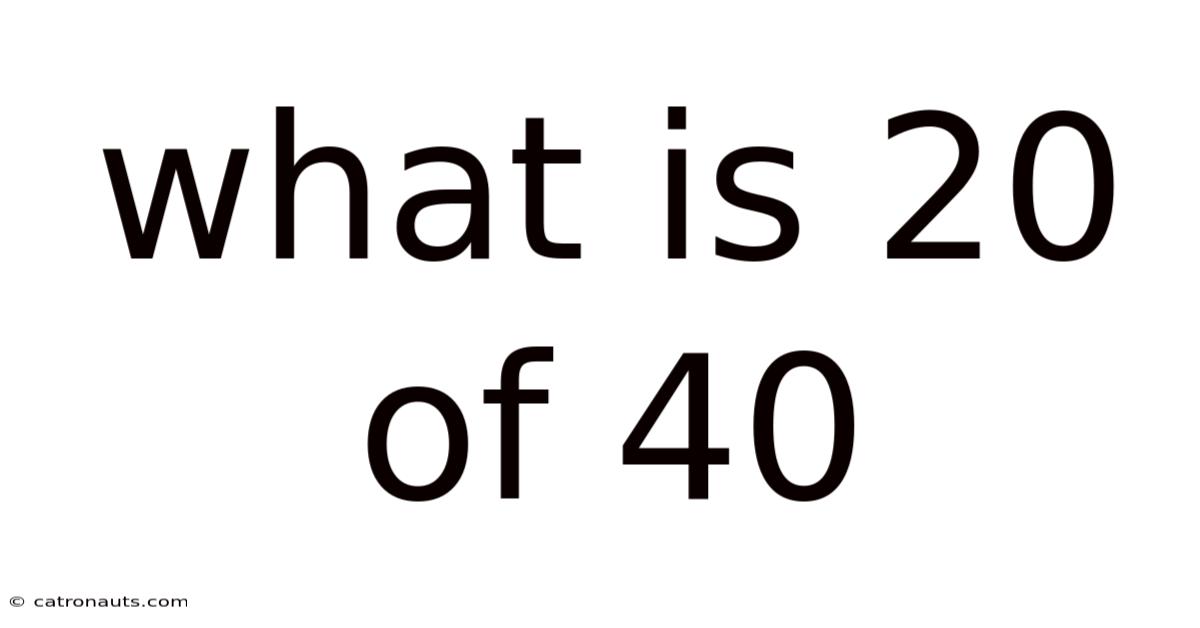
Table of Contents
What is 20 of 40? Deconstructing Fractions, Percentages, and Ratios
This seemingly simple question, "What is 20 of 40?", opens a door to a world of mathematical concepts crucial for everyday life. Understanding this seemingly basic calculation involves grasping fractions, percentages, and ratios – fundamental building blocks in arithmetic, algebra, and beyond. This article will not only answer the question directly but will also delve deeper into the underlying mathematical principles, offering a comprehensive understanding suitable for learners of all levels.
Understanding the Question: 20 of 40
At its core, "20 of 40" asks us to determine the relationship between the number 20 and the number 40. This relationship can be expressed in several ways, each offering a unique perspective:
- As a fraction: 20 out of 40 can be written as the fraction 20/40.
- As a percentage: This fraction represents a portion of the whole (40). We can convert this fraction to a percentage to express this portion more clearly.
- As a ratio: The relationship between 20 and 40 can be expressed as a ratio, 20:40.
Let's explore each of these representations in detail.
1. Expressing "20 of 40" as a Fraction
The simplest way to represent "20 of 40" is as a fraction: 20/40. A fraction shows a part of a whole. In this case, 20 is the part, and 40 is the whole.
To simplify this fraction, we find the greatest common divisor (GCD) of both the numerator (20) and the denominator (40). The GCD of 20 and 40 is 20. Dividing both the numerator and the denominator by the GCD, we get:
20/40 = (20 ÷ 20) / (40 ÷ 20) = 1/2
Therefore, 20 out of 40 is equal to 1/2. This simplified fraction is easier to understand and work with in further calculations.
2. Converting the Fraction to a Percentage
A percentage expresses a fraction as parts per hundred. To convert the fraction 1/2 to a percentage, we perform the following calculation:
(1/2) * 100% = 50%
Therefore, 20 out of 40 is equal to 50%. This means that 20 represents 50% of 40. Percentages are commonly used to represent proportions in various contexts, from calculating discounts to understanding statistical data.
3. Representing "20 of 40" as a Ratio
A ratio compares two quantities. The ratio of 20 to 40 is written as 20:40. Similar to fractions, ratios can be simplified by dividing both sides by their greatest common divisor (GCD), which is 20:
20:40 = (20 ÷ 20) : (40 ÷ 20) = 1:2
This simplified ratio, 1:2, shows that for every one unit of the first quantity, there are two units of the second quantity. Ratios are frequently used in various fields, including cooking recipes, map scales, and comparing different quantities.
Practical Applications and Real-World Examples
Understanding fractions, percentages, and ratios is crucial for navigating numerous real-world scenarios. Here are some examples illustrating the practical applications of the concept "20 of 40":
- Sales and Discounts: If a store offers a 50% discount on an item originally priced at $40, the discount amount is 20 dollars (50% of $40). This is a direct application of the percentage representation of 20 of 40.
- Test Scores: If a student answers 20 out of 40 questions correctly on a test, their score is 50%. Again, this highlights the relevance of percentage calculations in evaluating performance.
- Recipe Scaling: A recipe calls for 20 grams of flour for every 40 grams of sugar. The ratio of flour to sugar is 1:2, showcasing the practical application of ratios in cooking and baking.
- Data Analysis: In statistical analysis, understanding proportions and ratios is crucial for interpreting data and drawing meaningful conclusions. For example, if a survey shows that 20 out of 40 respondents prefer a certain product, it indicates a 50% preference rate.
- Probability: The concept of probability is closely related to fractions. If there are 40 equally likely outcomes and 20 of them are favorable, the probability of a favorable outcome is 20/40, or 1/2, or 50%.
Further Exploration: Beyond the Basics
While the question "What is 20 of 40?" appears simple, its resolution opens doors to more complex mathematical concepts. Consider these further explorations:
- Proportions: The relationship between 20 and 40 can be expressed as a proportion: 20/40 = x/100. Solving for x gives us the percentage value (50%). Proportions are powerful tools for solving problems involving equivalent ratios.
- Algebraic Equations: The problem can be framed as an algebraic equation: x/40 = 1/2. Solving for x gives us the value 20. This demonstrates how fractions can be used within algebraic expressions.
- Advanced Ratios and Proportions: The concepts of ratios and proportions extend to more complex scenarios involving multiple quantities and variables. Understanding these concepts is essential for advanced mathematical studies.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator to convert the fraction 20/40 to a decimal (0.5) and then multiply by 100 to get the percentage (50%). However, understanding the underlying principles of fractions, percentages, and ratios is more important than just getting the answer.
Q: What if the numbers were different? How would I solve similar problems?
A: The same principles apply. For any problem involving "X of Y," you would express it as a fraction (X/Y), simplify the fraction, convert it to a percentage (X/Y * 100%), and/or represent it as a ratio (X:Y).
Q: Are there any real-world scenarios where this calculation isn't helpful?
A: While the principles are widely applicable, situations with non-numerical or non-quantifiable attributes would not directly use these methods. For example, comparing subjective opinions or preferences wouldn’t involve fractions, percentages, or ratios in the same way.
Q: What are some common mistakes people make when working with fractions and percentages?
A: Common mistakes include incorrectly simplifying fractions, making errors during percentage calculations, and misinterpreting ratios. Careful attention to detail and a strong understanding of fundamental concepts are essential to avoid these errors.
Conclusion: Mastering Fundamental Concepts
The seemingly simple question, "What is 20 of 40?", serves as a springboard for exploring crucial mathematical concepts: fractions, percentages, and ratios. Mastering these concepts isn't just about solving equations; it's about developing a deeper understanding of how quantities relate to each other, a skill that's essential for problem-solving and critical thinking in numerous areas of life. From everyday budgeting to advanced scientific research, the ability to confidently work with fractions, percentages, and ratios is an invaluable asset. By understanding the underlying principles and practicing regularly, you can build a solid mathematical foundation for future learning and success.
Latest Posts
Latest Posts
-
Equation For Paired T Test
Sep 17, 2025
-
Convert 20 Pounds To Kilos
Sep 17, 2025
-
How Far Is 200 Meters
Sep 17, 2025
-
What Is Freedom Of Assembly
Sep 17, 2025
-
Tao Te Ching Best Translation
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.