What Is 20 Of 40.00
catronauts
Sep 17, 2025 · 6 min read
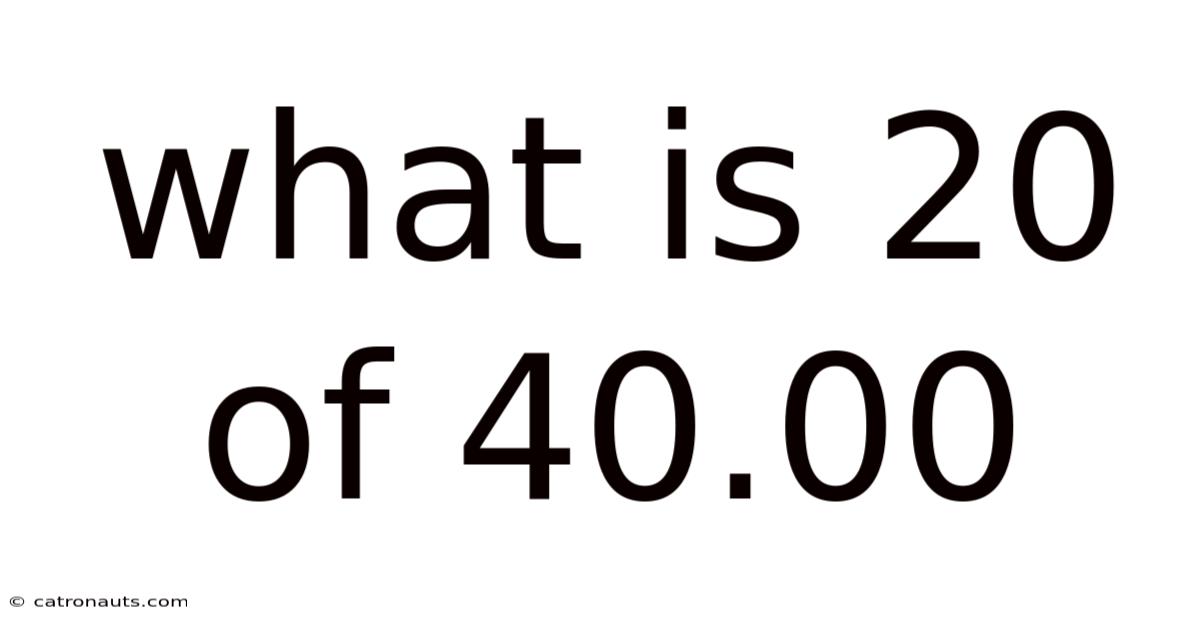
Table of Contents
What is 20 of 40.00? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 20 of 40.00?", opens the door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. While the immediate answer might seem obvious, exploring the various ways to interpret and solve this problem provides valuable insight into mathematical reasoning and problem-solving skills. This article will delve into the different approaches to finding the answer, explaining the underlying principles and demonstrating their broader applicability.
Understanding the Question
The phrasing "20 of 40.00" can be interpreted in a few ways, each leading to a different mathematical operation. The most common interpretation is to find what proportion 20 represents of the total 40.00. This can be expressed as a fraction, a percentage, or a ratio. Let's explore each approach.
1. The Fraction Approach: Expressing the Relationship as a Part of a Whole
The most straightforward approach is to express the relationship between 20 and 40.00 as a fraction. A fraction represents a part of a whole. In this case, 20 is the part, and 40.00 is the whole. Therefore, the fraction is:
20/40.00
To simplify this fraction, we can divide both the numerator (20) and the denominator (40.00) by their greatest common divisor, which is 20:
20 ÷ 20 = 1 40.00 ÷ 20 = 2
This simplifies the fraction to 1/2. Therefore, 20 is one-half (1/2) of 40.00. This fractional representation clearly illustrates the proportional relationship between the two numbers.
2. The Percentage Approach: Expressing the Relationship as a Proportion of 100
Percentages are a way of expressing a fraction as a proportion of 100. To find the percentage that 20 represents of 40.00, we can use the following formula:
(Part / Whole) * 100%
Substituting our values:
(20 / 40.00) * 100% = 0.5 * 100% = 50%
Therefore, 20 represents 50% of 40.00. This percentage representation is useful for comparing proportions and making relative comparisons across different datasets. For instance, understanding that 20 is 50% of 40 allows for easy comparisons to other percentages. If another value represented 75% of 40, it would immediately be clear that it’s a larger portion than 20.
3. The Ratio Approach: Comparing Two Quantities
A ratio is a comparison of two quantities. The ratio of 20 to 40.00 can be expressed as:
20:40.00
Similar to the fraction, we can simplify this ratio by dividing both numbers by their greatest common divisor (20):
20 ÷ 20 = 1 40.00 ÷ 20 = 2
The simplified ratio is 1:2. This ratio indicates that for every one unit of the first quantity (20), there are two units of the second quantity (40.00). Ratios are particularly useful in scenarios where we want to understand the relative relationship between two quantities, such as comparing the number of boys to girls in a classroom or the proportion of different ingredients in a recipe.
Expanding the Understanding: Practical Applications and Problem-Solving
The seemingly simple problem of "What is 20 of 40.00?" has far-reaching implications in various real-world scenarios. Understanding fractions, percentages, and ratios is crucial in numerous fields:
- Finance: Calculating interest rates, discounts, profit margins, and investment returns often involve working with percentages and ratios.
- Science: Expressing concentrations of solutions, analyzing experimental data, and understanding proportions in chemical reactions all require a solid grasp of these concepts.
- Engineering: Determining scaling factors, calculating material quantities, and analyzing structural ratios are critical aspects of engineering projects.
- Everyday Life: Understanding percentages is essential for budgeting, shopping (calculating discounts), and interpreting statistical data presented in news reports or surveys.
Beyond the Basics: Working with Decimals and More Complex Problems
The inclusion of the decimal in "40.00" doesn't fundamentally change the approach to solving the problem. The principles of fractions, percentages, and ratios remain the same, regardless of whether the numbers involved are whole numbers or decimals. However, working with decimals might involve additional steps, especially when dealing with more complex calculations.
For example, if the problem was "What is 17.5 of 40.00?", the calculations would involve decimals:
- Fraction: 17.5/40.00 = 0.4375 (This can be further expressed as a fraction such as 7/16)
- Percentage: (17.5/40.00) * 100% = 43.75%
- Ratio: 17.5:40.00 (Simplified to approximately 7:16 after converting to a fraction)
This demonstrates that the process is consistent even when decimals are involved. The key is to maintain accuracy during calculations and understand how to simplify the resulting fractions or ratios.
Frequently Asked Questions (FAQ)
Q: Why is it important to simplify fractions and ratios?
A: Simplifying fractions and ratios makes them easier to understand and compare. A simplified fraction or ratio represents the same proportional relationship as the original, but in a more concise and manageable form.
Q: Can I use a calculator to solve these problems?
A: Yes, calculators can be very helpful in performing the calculations involved in determining fractions, percentages, and ratios, especially when dealing with larger numbers or decimals. However, understanding the underlying principles is crucial to ensure that you use the calculator correctly and interpret the results accurately.
Q: What if the "whole" number is smaller than the "part"?
A: If the "part" is larger than the "whole," the resulting fraction, percentage, or ratio will be greater than 1 or 100%. This indicates that the "part" exceeds the "whole," which might represent an error in the data or a different context where the "whole" represents a base or reference point rather than a true total.
Q: Are there other ways to solve this type of problem?
A: Yes. Proportions can also be used to solve this type of problem. Setting up a proportion allows you to find the unknown value given three known values. For example:
20/40 = x/100 (To find the percentage, we set up a proportion with 100 as the denominator to represent the total percentage)
Solving for x will yield 50, indicating that 20 is 50% of 40.
Conclusion: Mastering the Fundamentals
Understanding "What is 20 of 40.00?" goes beyond finding a simple numerical answer. It's about mastering the fundamental concepts of fractions, percentages, and ratios. These concepts are the building blocks for more advanced mathematical skills and are essential for success in various academic and professional fields. By grasping these concepts, you'll not only be able to solve similar problems but also develop a deeper understanding of how to approach and solve a wide range of mathematical problems in various contexts. The ability to interpret and manipulate these concepts with ease will equip you with valuable problem-solving skills that extend far beyond the classroom or workplace. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
What Is A Political Theory
Sep 17, 2025
-
Difference Between Team And Group
Sep 17, 2025
-
Trojan War Epic Crossword Clue
Sep 17, 2025
-
How Does King Arthur Die
Sep 17, 2025
-
How To Write A Rap
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 40.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.