What Is 25 Of 16
catronauts
Sep 10, 2025 · 6 min read
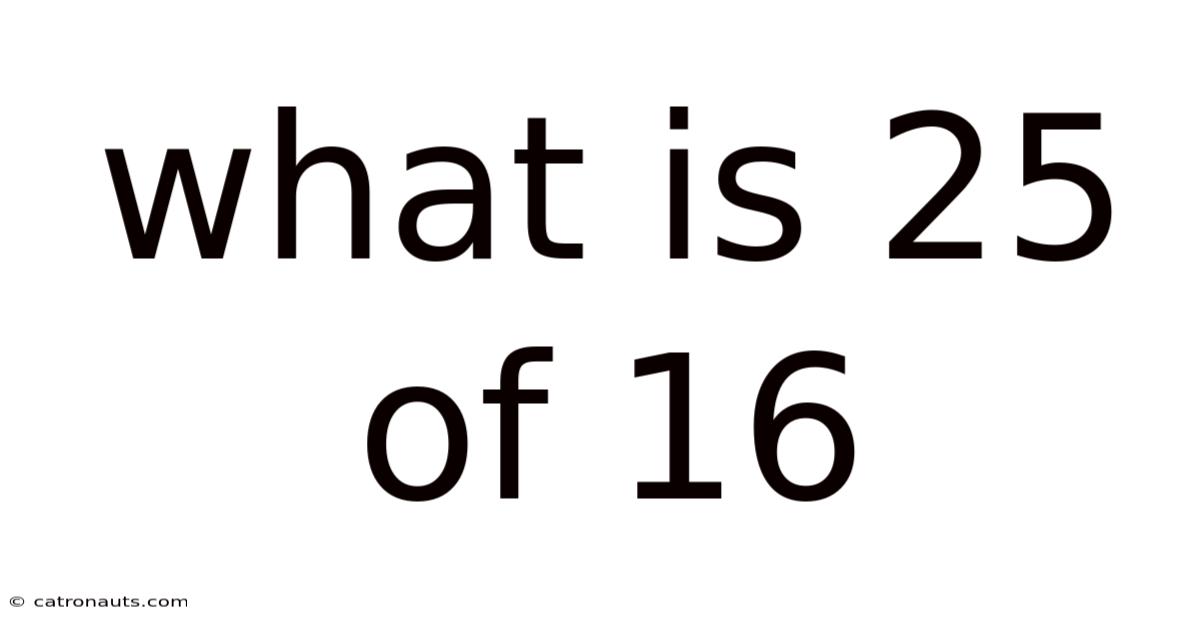
Table of Contents
What is 25% of 16? A Comprehensive Guide to Percentages and Their Applications
Understanding percentages is a fundamental skill applicable in numerous everyday situations, from calculating discounts and taxes to comprehending statistical data and financial reports. This article will not only answer the question "What is 25% of 16?" but will also delve into the underlying principles of percentage calculations, offering a comprehensive guide for all levels of understanding. We'll explore different methods for solving percentage problems, providing practical examples and clarifying common misconceptions. By the end, you'll be confident in calculating percentages and applying this knowledge to various real-world scenarios.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ("per cent" in Latin). Therefore, 25% signifies 25 parts out of 100 equal parts of a whole. This can be represented as a fraction (25/100) or a decimal (0.25). Understanding this basic concept is crucial to solving percentage problems.
Method 1: Converting Percentage to Fraction
The most straightforward way to calculate 25% of 16 is to convert the percentage into a fraction and then perform the multiplication.
-
Step 1: Convert the percentage to a fraction: 25% can be written as 25/100.
-
Step 2: Simplify the fraction (if possible): 25/100 simplifies to 1/4. This is because both the numerator and denominator are divisible by 25.
-
Step 3: Multiply the fraction by the whole number: (1/4) * 16 = 4
Therefore, 25% of 16 is 4.
Method 2: Converting Percentage to Decimal
Another common method involves converting the percentage to a decimal before multiplying.
-
Step 1: Convert the percentage to a decimal: To convert a percentage to a decimal, divide the percentage by 100. 25% divided by 100 equals 0.25.
-
Step 2: Multiply the decimal by the whole number: 0.25 * 16 = 4
Again, we arrive at the answer: 25% of 16 is 4.
Method 3: Using Proportions
This method is particularly useful for understanding the relationship between the percentage, the part, and the whole. We can set up a proportion:
- Part / Whole = Percentage / 100
Let 'x' represent 25% of 16. We can set up the proportion as follows:
x / 16 = 25 / 100
To solve for 'x', we can cross-multiply:
100x = 25 * 16
100x = 400
x = 400 / 100
x = 4
Therefore, 25% of 16 is 4.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in many real-world contexts. Here are a few examples:
-
Discounts: If a store offers a 25% discount on an item priced at $16, you would calculate 25% of $16 ($4) and subtract that amount from the original price ($16 - $4 = $12). The final price would be $12.
-
Taxes: If a sales tax is 6%, and you buy an item for $100, you would calculate 6% of $100 ($6) and add that to the original price ($100 + $6 = $106). The total cost would be $106.
-
Tips: Calculating a tip in a restaurant often involves percentages. A 15% tip on a $40 meal is calculated as 15% of $40, which is $6.
-
Interest Rates: Understanding interest rates on loans or savings accounts requires percentage calculations. A 5% interest rate on a $1000 loan means you'll pay $50 in interest in the first year (5% of $1000).
-
Data Analysis: Percentages are frequently used to represent data in charts and graphs, making it easier to visualize and understand trends and proportions. For example, a survey might show that 30% of respondents prefer a certain product.
-
Financial Statements: Businesses use percentages extensively in financial reporting to represent profit margins, revenue growth, and expense ratios.
Solving More Complex Percentage Problems
While the example of 25% of 16 is relatively simple, the principles can be applied to more complex scenarios. For instance, if you need to calculate 17.5% of 85, you can use any of the methods described above. Simply convert 17.5% to a decimal (0.175) or a fraction (175/1000), and multiply by 85. This will give you the answer: 14.875.
Similarly, if you need to find what percentage a certain number represents of another number, you can reverse the process. For example, if 6 is what percentage of 24? You would set up the equation: x/100 = 6/24, and solve for x, finding that 6 is 25% of 24.
Common Mistakes to Avoid When Working with Percentages
-
Confusing percentage increase and percentage of: A 25% increase on a value is different from 25% of that value. A 25% increase on 16 would be 16 + (0.25 * 16) = 20.
-
Incorrect decimal placement: Always ensure you correctly place the decimal point when converting between percentages and decimals. 0.25 is different from 2.5 or 25.
-
Rounding errors: When working with decimals, be mindful of rounding errors, especially when dealing with financial calculations where precision is critical.
-
Failing to consider the whole: Remember that the percentage always refers to a specific whole. Clearly identifying the whole is crucial for accurate calculation.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method often depends on individual preference and the specific problem. Converting to a decimal and multiplying is generally quick and efficient for many situations.
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new value and the original value, then divide this difference by the original value, and finally, multiply by 100 to get the percentage increase. For a percentage decrease, follow the same steps, but the result will be negative.
Q: Can I use a calculator for percentage calculations?
A: Yes, most calculators have a percentage function (%) that simplifies these calculations. However, understanding the underlying principles is still essential.
Q: Are there online tools for percentage calculations?
A: Yes, many online calculators and websites are available to assist with percentage calculations. However, understanding the methodology remains important for problem-solving and critical thinking.
Conclusion
Calculating percentages is a fundamental mathematical skill with broad applications in various aspects of daily life and professional fields. This comprehensive guide provides different methods for accurately calculating percentages and addresses common misconceptions. By mastering these techniques, you'll not only be able to confidently answer questions like "What is 25% of 16?" but also tackle more complex percentage problems with ease, enhancing your analytical and problem-solving abilities. Remember to practice regularly to solidify your understanding and build your confidence in tackling percentage-related tasks. Through consistent practice and a solid grasp of the underlying principles, you'll become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
Formula For Coefficient Of Restitution
Sep 10, 2025
-
Food Web In The Amazon
Sep 10, 2025
-
Iron On Table Of Elements
Sep 10, 2025
-
What Is In Urea Fertilizer
Sep 10, 2025
-
Reviews On The Alchemist Book
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.