What Is 30 Of 90
catronauts
Sep 13, 2025 · 5 min read
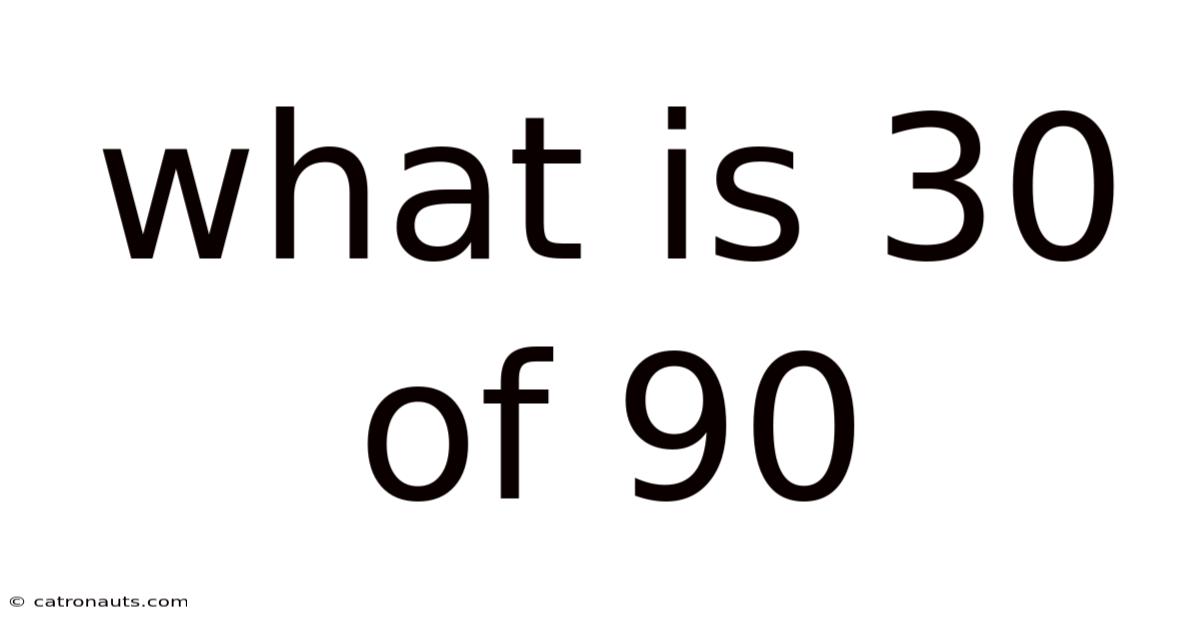
Table of Contents
What is 30% of 90? A Comprehensive Guide to Percentages and Their Applications
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and making informed decisions. This article will comprehensively explore the question "What is 30% of 90?" and delve into the broader concepts of percentages, providing you with a solid understanding of this essential mathematical concept. We'll cover the calculation methods, real-world applications, and even touch upon the underlying mathematical principles.
Understanding Percentages
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). It's a way to represent a part of a whole in a standardized, easily comparable format. For example, 50% represents 50 out of 100, or one-half. Similarly, 25% represents 25 out of 100, or one-quarter.
Calculating 30% of 90: Three Methods
There are several ways to calculate 30% of 90. Let's explore three common methods:
Method 1: Using the Fraction Method
This method converts the percentage to a fraction and then multiplies it by the whole number. Remember that 30% can be written as the fraction 30/100, which simplifies to 3/10.
Therefore, 30% of 90 is:
(3/10) * 90 = 27
Method 2: Using Decimal Conversion
This method converts the percentage to a decimal and then multiplies it by the whole number. To convert 30% to a decimal, divide it by 100:
30% / 100 = 0.30
Now, multiply the decimal by 90:
0.30 * 90 = 27
Method 3: Using Proportions
This method sets up a proportion to solve for the unknown value. We can set up the proportion as follows:
30/100 = x/90
To solve for x (which represents 30% of 90), cross-multiply:
30 * 90 = 100 * x
2700 = 100x
x = 2700 / 100
x = 27
Therefore, 30% of 90 is 27.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in many everyday situations. Here are a few examples:
-
Shopping: Calculating discounts, sales tax, and tips. If a store offers a 30% discount on an item that costs $90, you'd save $27 (30% of $90).
-
Finance: Determining interest rates, loan repayments, and investment returns. Understanding percentage changes in stock prices or interest earned on savings accounts is essential for financial planning.
-
Science and Statistics: Representing data, analyzing trends, and making predictions. Percentages are frequently used in scientific research, statistical analysis, and data visualization.
-
Grading and Assessments: Calculating grades based on scores, determining student performance, and evaluating learning outcomes. Many educational institutions use percentages to represent student progress and achievement.
-
Everyday Life: Calculating recipes (e.g., increasing or decreasing ingredient quantities), understanding survey results (e.g., the percentage of people who prefer a particular brand), and many other daily tasks.
Understanding Percentage Increase and Decrease
It's important to distinguish between finding a percentage of a number and finding a percentage increase or decrease.
-
Percentage of a number: This is what we've been calculating so far. It finds a specific part of a whole.
-
Percentage increase: This calculates the increase in a value as a percentage of the original value. For example, if a value increases from 90 to 108, the percentage increase is calculated as follows:
((108 - 90) / 90) * 100% = 20%
-
Percentage decrease: This calculates the decrease in a value as a percentage of the original value. For example, if a value decreases from 90 to 63, the percentage decrease is calculated as follows:
((90 - 63) / 90) * 100% = 30%
Advanced Applications: Compound Interest and Exponential Growth
Percentages are fundamental to understanding concepts like compound interest and exponential growth. Compound interest, commonly used in savings accounts and loans, calculates interest on both the principal amount and accumulated interest from previous periods. The impact of compounding can be substantial over time. Similarly, exponential growth models (often represented with percentage growth rates) describe situations where a quantity grows proportionally to its current value. This is observed in various phenomena, including population growth and the spread of certain diseases.
Frequently Asked Questions (FAQs)
Q: How can I calculate percentages quickly without a calculator?
A: For certain percentages, mental math tricks are helpful. For instance, 10% of a number is simply the number divided by 10. 5% is half of 10%, and so on. You can use these base percentages to estimate other percentages.
Q: What if I need to calculate a percentage of a number that isn't a whole number?
A: The methods remain the same. Simply replace the whole number with the decimal value and follow the steps outlined above.
Q: Are there any online calculators or tools that can help me calculate percentages?
A: Yes, numerous online percentage calculators are available that can perform these calculations quickly and accurately.
Q: How do I reverse a percentage calculation? For example, if 27 is 30% of a number, what is that number?
A: To find the original number, you can set up a proportion:
27/x = 30/100
Solving for x, you get x = 90. Alternatively, you can divide 27 by 0.30 (the decimal equivalent of 30%).
Conclusion: Mastering Percentages for Success
Understanding percentages is an invaluable skill that transcends academic settings and permeates many aspects of our daily lives. This comprehensive guide has demonstrated the fundamental principles of percentage calculations, explored different calculation methods, and illustrated various real-world applications. Mastering this concept will not only improve your problem-solving skills but also empower you to make more informed decisions in finance, shopping, and various other areas. Remember the three methods discussed – fraction method, decimal conversion, and proportion method – to tackle any percentage problem with confidence. By understanding these concepts and practicing regularly, you'll be well-equipped to confidently navigate the world of percentages and leverage this knowledge for personal and professional success.
Latest Posts
Latest Posts
-
How To Remove A Log
Sep 13, 2025
-
Twelve Angry Men Juror 10
Sep 13, 2025
-
Rude Words Starting With M
Sep 13, 2025
-
Shri Guru Nanak Dev Ji
Sep 13, 2025
-
My Name Is In Germany
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.