What Is 40 Of 80
catronauts
Sep 16, 2025 · 5 min read
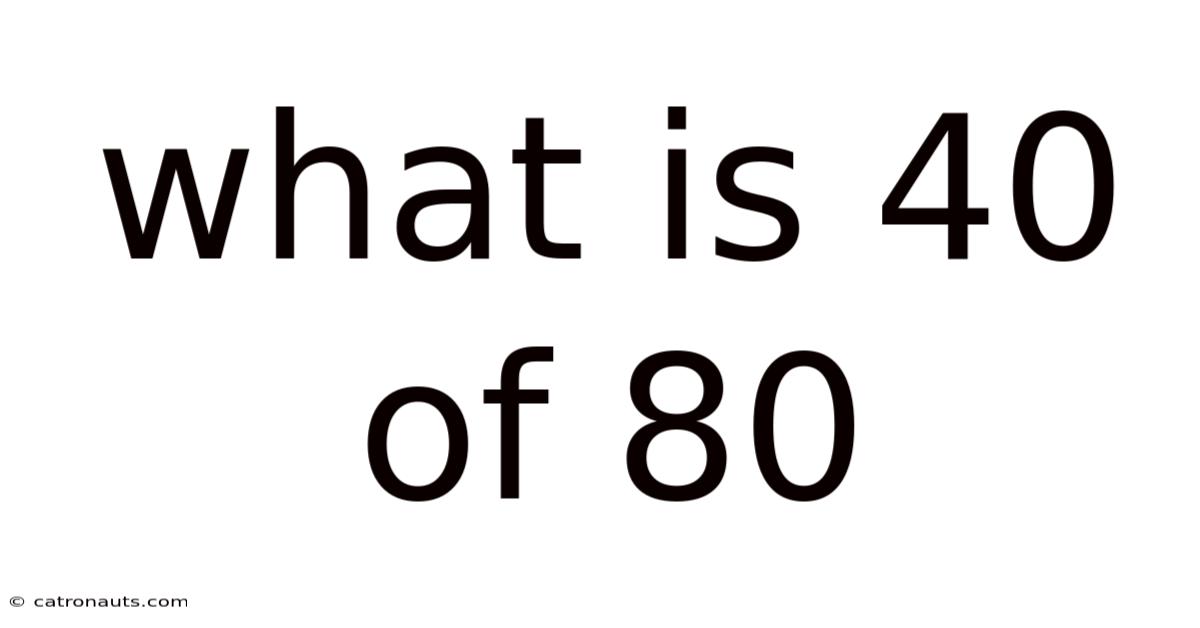
Table of Contents
What is 40 of 80? Deconstructing Percentages, Fractions, and Ratios
This article explores the question "What is 40 of 80?" in a comprehensive way, going beyond a simple numerical answer to delve into the underlying concepts of percentages, fractions, and ratios. Understanding these fundamental mathematical principles is crucial for various applications in everyday life, from calculating discounts to analyzing data. We'll also explore the practical implications and real-world scenarios where this type of calculation is used.
Introduction: Understanding the Problem
The question, "What is 40 of 80?" can be interpreted in several ways, primarily focusing on the relationship between 40 and 80. It's essentially asking us to determine the proportional relationship between these two numbers. This can be expressed as a fraction, a percentage, or a ratio, all of which are interconnected mathematical concepts. We'll explore each representation to gain a complete understanding of the solution and the underlying mathematical principles.
Method 1: Using Fractions
The simplest approach to understanding "40 of 80" is to express it as a fraction. This represents the part (40) in relation to the whole (80). Therefore, the fraction is 40/80.
To simplify this fraction, we find the greatest common divisor (GCD) of 40 and 80, which is 40. Dividing both the numerator and the denominator by 40, we get:
40/80 = 1/2
This simplified fraction, 1/2, means that 40 represents one-half of 80.
Method 2: Calculating Percentages
Percentages provide another way to express the relationship between 40 and 80. A percentage shows the proportion of a number out of 100. To calculate the percentage, we can use the following formula:
(Part / Whole) * 100%
In this case:
(40 / 80) * 100% = 0.5 * 100% = 50%
Therefore, 40 is 50% of 80.
Method 3: Using Ratios
A ratio expresses the relationship between two or more quantities. The ratio of 40 to 80 can be written as 40:80. Similar to fractions, we can simplify this ratio by dividing both numbers by their GCD (40):
40:80 = 1:2
This simplified ratio, 1:2, indicates that for every one unit of the first quantity, there are two units of the second quantity. This is consistent with the fraction and percentage calculations, confirming that 40 is half of 80.
Real-World Applications: Where This Calculation Matters
The seemingly simple calculation of "40 of 80" has numerous real-world applications across various fields:
-
Discount Calculations: Imagine a store offering a 50% discount on an item originally priced at $80. The discount amount is calculated as 50% of $80, which is (50/100) * $80 = $40. This directly relates to our original problem.
-
Progress Tracking: If a project has 80 tasks, and 40 tasks are completed, the progress is 50% complete. This is a straightforward application of percentage calculation.
-
Data Analysis: In statistical analysis, understanding proportions is vital. If a survey of 80 people shows 40 prefer a particular product, that represents 50% preference.
-
Recipe Scaling: If a recipe calls for 80 grams of flour and you want to halve the recipe, you would use 40 grams of flour.
-
Financial Management: Determining the portion of a budget allocated to different expenses involves similar calculations. If your total budget is $80 and you spend $40 on groceries, that's 50% of your budget.
Expanding the Understanding: Proportions and Proportional Reasoning
The problem "40 of 80" is a prime example of a proportional relationship. Proportional reasoning is a crucial skill that involves understanding the relationship between different quantities and how changes in one quantity affect another. This skill is fundamental in various areas, including:
-
Scaling maps: Understanding scale is a direct application of proportional reasoning.
-
Converting units: Converting between different units (e.g., kilometers to miles) requires understanding the proportional relationship between the units.
-
Solving problems involving rates: Calculating speed, distance, and time relies on proportional reasoning.
-
Geometry and trigonometry: Many geometric and trigonometric calculations involve proportions.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, absolutely. A calculator can quickly provide the answer to 40/80, or the percentage equivalent. However, understanding the underlying mathematical principles is more important than just getting the numerical answer.
Q: What if the numbers were different? How would I approach a similar problem?
A: The same methods—fractions, percentages, and ratios—can be applied to any similar problem involving finding a part of a whole. Simply replace 40 and 80 with the new numbers and follow the same steps.
Q: Why is understanding fractions, percentages, and ratios important?
A: These are fundamental mathematical concepts used in countless everyday situations, from shopping to financial planning to scientific analysis. Mastering these concepts empowers you to solve a wide range of problems efficiently and effectively.
Further Exploration: Beyond the Basics
While the solution to "40 of 80" is straightforward, the underlying mathematical concepts are far-reaching. Further exploration might involve:
-
Advanced percentage calculations: Working with compound interest, discounts, and taxes involves more complex percentage calculations.
-
Algebraic representation of proportions: Expressing proportional relationships using algebraic equations.
-
Statistical analysis involving proportions: Understanding confidence intervals and hypothesis testing related to proportions.
Conclusion: Mastering Proportions for a Brighter Future
In conclusion, "40 of 80" is equal to 1/2, 50%, or a 1:2 ratio. While the numerical answer is simple, the journey to reach this answer highlights the importance of understanding fractions, percentages, and ratios—fundamental mathematical concepts applicable to various real-world situations. Mastering these concepts not only improves your mathematical skills but also equips you with essential tools for problem-solving and critical thinking in many aspects of life. Understanding these basic principles builds a solid foundation for tackling more complex mathematical challenges and unlocks a deeper appreciation for the interconnectedness of mathematical ideas.
Latest Posts
Latest Posts
-
47 Out Of 60 Percentage
Sep 16, 2025
-
How Long Is The Quran
Sep 16, 2025
-
Sylvia Plath Poem Daddy Analysis
Sep 16, 2025
-
Surface Area And Area Formulas
Sep 16, 2025
-
Victims Of Crime South Australia
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.