What Is 75 Of 450
catronauts
Sep 19, 2025 · 6 min read
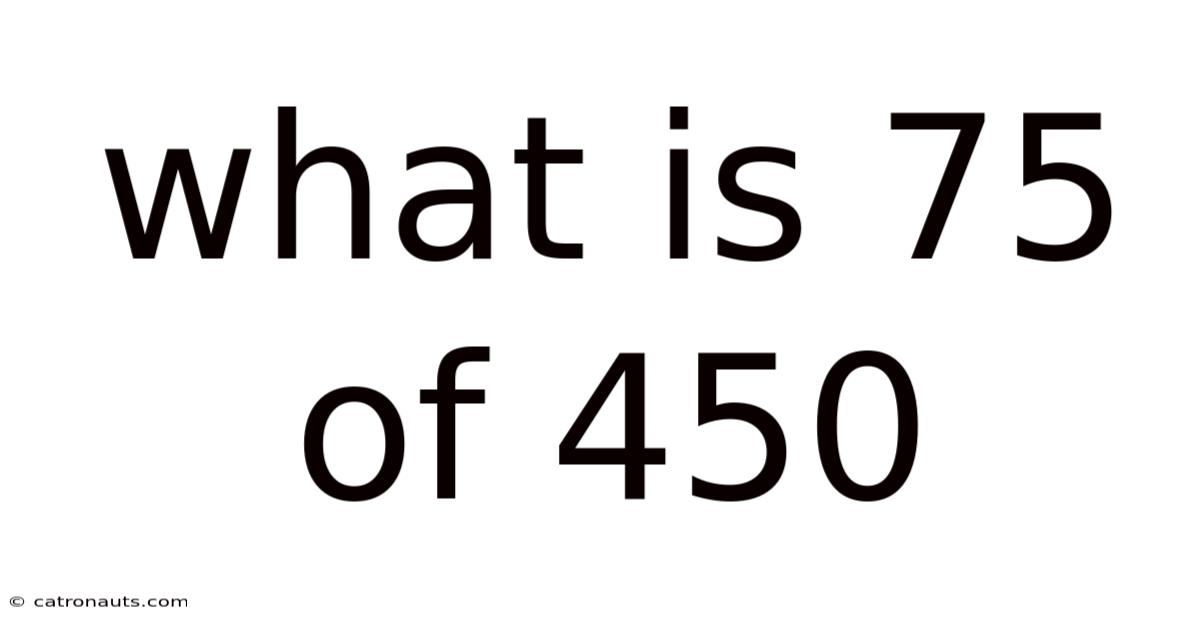
Table of Contents
What is 75% of 450? A Deep Dive into Percentages and Their Applications
Finding 75% of 450 might seem like a simple arithmetic problem, but it opens the door to understanding a crucial mathematical concept: percentages. This seemingly basic calculation is fundamental to countless real-world applications, from calculating discounts and sales tax to understanding financial reports and analyzing data. This article will not only show you how to calculate 75% of 450, but also explore the underlying principles of percentages, providing you with a robust understanding you can apply in various contexts.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ( per cent). So, 75% means 75 out of 100, or 75/100. This can be simplified to 3/4. Understanding this fundamental concept is key to solving percentage problems.
Calculating 75% of 450: Three Methods
There are several ways to calculate 75% of 450. Let's explore three common methods:
Method 1: Using Fractions
Since 75% is equivalent to 3/4, we can express the problem as finding 3/4 of 450. This is done through simple multiplication:
(3/4) * 450 = 1350/4 = 337.5
Therefore, 75% of 450 is 337.5.
Method 2: Using Decimal Equivalents
Percentages can also be represented as decimals. To convert a percentage to a decimal, divide the percentage by 100. 75% divided by 100 is 0.75. Now, we can multiply this decimal by 450:
0.75 * 450 = 337.5
Again, we find that 75% of 450 is 337.5.
Method 3: Using Proportions
This method is particularly helpful for understanding the underlying relationship between percentages and the whole. We can set up a proportion:
75/100 = x/450
Where 'x' represents the unknown value (75% of 450). To solve for 'x', we cross-multiply:
75 * 450 = 100 * x
33750 = 100x
x = 33750 / 100 = 337.5
Once more, we arrive at the answer: 75% of 450 is 337.5.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world scenarios. Here are a few examples:
-
Sales and Discounts: Stores frequently advertise sales, offering discounts like "25% off" or "75% off." Understanding percentages allows you to quickly calculate the final price after the discount. For instance, if a $450 item is discounted by 75%, you'd save $337.50 (as we calculated above), resulting in a final price of $112.50.
-
Taxes: Sales tax is added to the price of goods and services. Knowing how to calculate percentages helps you determine the total cost including tax. If the sales tax in your area is 6%, and you buy an item for $450, you would calculate 6% of $450 to find the tax amount and add it to the original price.
-
Interest Rates: Interest rates are expressed as percentages. Understanding percentages is essential for calculating interest earned on savings accounts or interest paid on loans. For example, if you invest $450 with a 5% annual interest rate, you would earn $22.50 in interest after one year.
-
Financial Statements: Companies use percentages extensively in financial statements. Profit margins, revenue growth rates, and debt-to-equity ratios are all expressed as percentages, allowing for easy comparison and analysis of performance over time or between different companies.
-
Data Analysis: Percentages are used to represent proportions and trends in data analysis. For example, if a survey shows that 75% of respondents prefer a certain product, you can interpret this to mean three out of four people prefer that specific item.
-
Tip Calculations: When dining out, calculating a tip (usually a percentage of the bill) is a common application of percentages.
Expanding Your Understanding: Beyond Basic Percentage Calculations
While calculating 75% of 450 is straightforward, the concepts involved extend far beyond this single calculation. Here are some related concepts to explore:
-
Calculating the Percentage One Number Represents of Another: Instead of finding a percentage of a number, you might need to find what percentage one number represents of another. For example, what percentage of 600 is 150? This involves dividing the smaller number by the larger number and multiplying by 100. In this case, 150/600 * 100 = 25%.
-
Percentage Increase and Decrease: These calculations help you determine the percentage change between two numbers. For example, if a quantity increases from 300 to 450, the percentage increase is calculated as [(450-300)/300] * 100 = 50%. Percentage decreases are calculated similarly.
-
Compound Interest: This involves calculating interest on the principal amount plus accumulated interest. Understanding compound interest is critical for long-term financial planning.
-
Working with Percentages in Spreadsheets: Spreadsheets like Microsoft Excel or Google Sheets offer built-in functions to calculate percentages, making large-scale calculations much easier.
Frequently Asked Questions (FAQ)
Q: What if the percentage isn't a whole number, like 75.5%?
A: You can use the same methods as described above, replacing 0.75 with 0.755 in the decimal method or adapting the fraction accordingly (75.5/100 = 0.755).
Q: How do I calculate the percentage of something that’s already been discounted?
A: First, calculate the discount. Then, subtract this from the original price to find the discounted price. If you need to apply another discount on top of that, use the discounted price as your new base amount.
Q: Are there any online calculators or tools that can help with percentage calculations?
A: Yes, many free online calculators are available that can help you with various percentage calculations. These can be useful for double-checking your work or for handling more complex scenarios. However, understanding the underlying principles is still crucial for applying the concepts effectively.
Q: Why is it important to understand percentages?
A: Percentages are a fundamental part of mathematics and are widely used in everyday life, finance, and various professional fields. A strong grasp of percentages empowers you to make informed decisions, analyze data effectively, and understand the financial implications of various scenarios.
Conclusion
Calculating 75% of 450, which equals 337.5, is a stepping stone to a much broader understanding of percentages. This simple calculation serves as a gateway to mastering a fundamental mathematical concept with vast applications in real-world contexts. From navigating daily shopping experiences to comprehending complex financial reports, a solid grasp of percentages is an essential skill that will benefit you in countless ways. By exploring the different methods of calculation and related concepts, you can build a robust foundation in this vital area of mathematics. Remember to practice applying these methods in various contexts to solidify your understanding and improve your problem-solving abilities.
Latest Posts
Latest Posts
-
Words That Rhyme With Fire
Sep 19, 2025
-
45 Degree Celsius To Fahrenheit
Sep 19, 2025
-
Atacama Desert South America Map
Sep 19, 2025
-
Amaranta 100 Years Of Solitude
Sep 19, 2025
-
Ch Words Sound Like K
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.