Whats 20 Percent Of 300
catronauts
Sep 18, 2025 · 6 min read
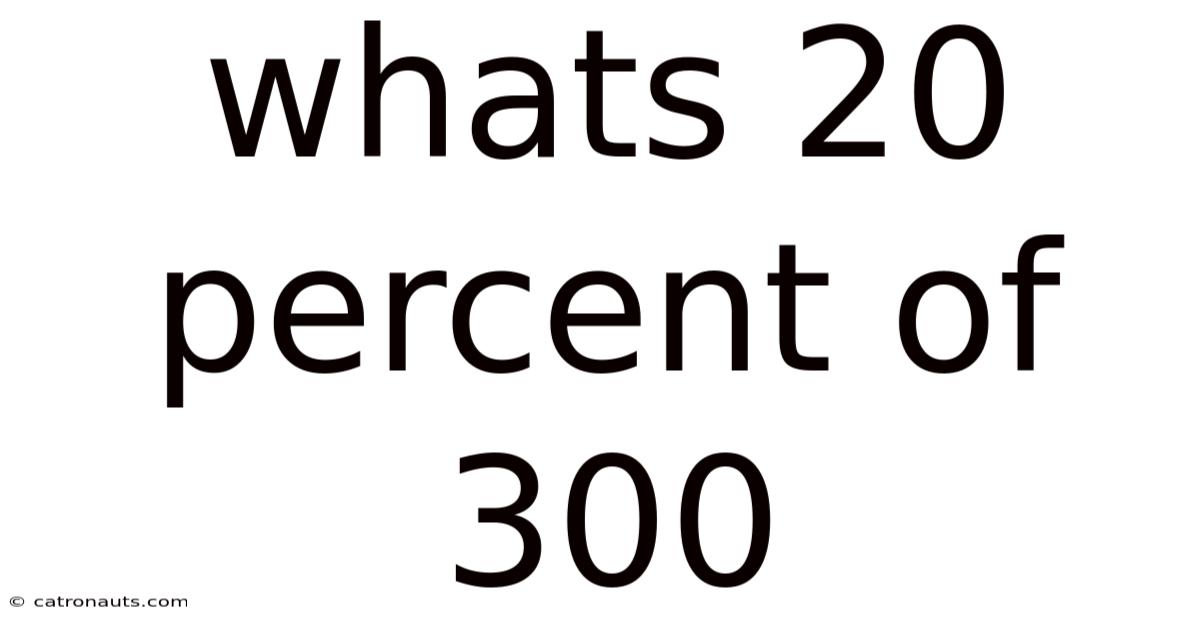
Table of Contents
What's 20 Percent of 300? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 300 might seem like a simple calculation, a quick task for a calculator. But understanding how to arrive at this answer, and more importantly, why the calculation works, opens the door to a broader understanding of percentages – a fundamental concept in mathematics with wide-ranging applications in everyday life, from finance and shopping to science and statistics. This article will not only provide the answer but will also explore the underlying principles, different methods of calculation, and real-world examples to solidify your grasp of percentages.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." So, 20 percent (often written as 20%) means 20 out of 100, or 20/100. This fraction can be simplified to 1/5. Understanding this foundational relationship is crucial for solving percentage problems.
Calculating 20 Percent of 300: Three Methods
There are several ways to calculate 20% of 300. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is perhaps the most straightforward method. To find a percentage of a number, we convert the percentage to its decimal equivalent by dividing by 100. In this case:
20% = 20/100 = 0.20
Then, we multiply this decimal by the number we're interested in:
0.20 * 300 = 60
Therefore, 20% of 300 is 60.
Method 2: Using Fractions
As mentioned earlier, 20% is equivalent to the fraction 1/5. We can use this fraction to calculate 20% of 300:
(1/5) * 300 = 300/5 = 60
Again, we find that 20% of 300 is 60. This method is particularly useful when dealing with percentages that have simple fractional equivalents, like 25% (1/4), 50% (1/2), and 75% (3/4).
Method 3: Proportion Method
The proportion method is a more general approach that can be applied to any percentage calculation. We set up a proportion:
Part / Whole = Percentage / 100
In our case:
x / 300 = 20 / 100
To solve for x (20% of 300), we cross-multiply:
100*x = 20 * 300
100*x = 6000
x = 6000 / 100
x = 60
So, once again, we find that 20% of 300 is 60. This method is helpful for understanding the relationship between the parts and the whole and is easily adaptable to more complex problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a vital skill with numerous applications across various fields:
-
Finance: Calculating interest on loans, savings accounts, and investments; determining discounts on purchases; understanding tax rates; analyzing financial statements. For example, if you invest $300 and earn a 20% return, you would gain $60.
-
Shopping: Determining the final price of items after discounts; comparing prices of similar products; budgeting for expenses. A 20% discount on a $300 item would mean a savings of $60, reducing the final price to $240.
-
Science: Representing experimental data; expressing changes in quantities (e.g., population growth or decline); calculating concentrations of solutions. A 20% increase in a scientific measurement might signify significant changes depending on the context.
-
Statistics: Analyzing data sets; presenting results in a meaningful way; understanding probability and risk. A 20% chance of rain, for instance, indicates a significant probability of precipitation.
-
Everyday Life: Calculating tips in restaurants; determining the amount of ingredients needed for recipes (scaling recipes up or down); understanding nutritional information on food labels. A 20% tip on a $300 restaurant bill would be $60.
Beyond the Basics: More Complex Percentage Problems
While finding 20% of 300 is a relatively straightforward calculation, percentage problems can become more complex. For instance:
-
Finding the original amount: If an item is discounted by 20% and costs $240, what was the original price? This involves working backward from the discounted price.
-
Calculating percentage increase or decrease: If a quantity increases from 300 to 360, what is the percentage increase? This requires calculating the difference, then expressing that difference as a percentage of the original amount.
-
Compound percentages: Calculating the effect of multiple percentage changes applied sequentially (e.g., a 10% increase followed by a 5% decrease). Compound percentages require careful step-by-step calculations.
Addressing Common Errors and Misconceptions
Even seemingly simple percentage calculations can lead to errors if certain pitfalls are not avoided:
-
Incorrect decimal conversion: Failing to correctly convert a percentage to a decimal (e.g., writing 20% as 0.2 instead of 0.20) can lead to incorrect results.
-
Mixing up percentages and decimals: Confusing percentage values with decimal values is a common mistake. Always ensure the correct units are used throughout the calculation.
-
Incorrect application of formulas: Misunderstanding the application of percentage formulas, particularly when dealing with percentage increases or decreases, can lead to inaccuracies.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method often depends on the specific problem. The decimal method is generally quick and efficient for most calculations, while the fractional method is useful for percentages with simple fractional equivalents. The proportion method offers a more general and adaptable approach.
Q: How can I improve my percentage calculation skills?
A: Practice is key! Work through various percentage problems of increasing complexity. Understanding the underlying principles, particularly the relationship between fractions, decimals, and percentages, is vital.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, numerous online calculators are available that can perform percentage calculations. These tools can be helpful for checking your work or for solving more complex problems. However, understanding the methods behind the calculations is crucial for building a strong foundation in mathematics.
Q: What if I need to calculate a percentage of a number that isn't a whole number?
A: The methods described above work equally well for non-whole numbers. Simply replace the whole number with your decimal value and proceed with the calculation as usual. For example, finding 20% of 300.5 would involve multiplying 0.20 by 300.5.
Q: How do I calculate a percentage change?
A: To calculate a percentage change, find the difference between the new value and the original value. Then, divide this difference by the original value and multiply by 100. The result is the percentage change. If the result is positive, it is a percentage increase; if it's negative, it's a percentage decrease.
Conclusion
Determining that 20% of 300 is 60 is just the starting point. This seemingly simple calculation opens a door to a deeper understanding of percentages, their importance in diverse fields, and the various methods for their calculation. By mastering these fundamental concepts and practicing various problem types, you'll build a solid foundation in mathematics and enhance your ability to tackle real-world problems that involve percentages. Remember that consistent practice and a clear understanding of the underlying principles are key to success in mastering percentage calculations.
Latest Posts
Latest Posts
-
Inverting And Noninverting Op Amp
Sep 18, 2025
-
To Kill A Mockingbird Themes
Sep 18, 2025
-
Multiplication And Division Fact Families
Sep 18, 2025
-
Trobriand Islands Papua New Guinea
Sep 18, 2025
-
How To Write Your Autobiography
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.