Whats 40 Percent Of 60
catronauts
Sep 16, 2025 · 5 min read
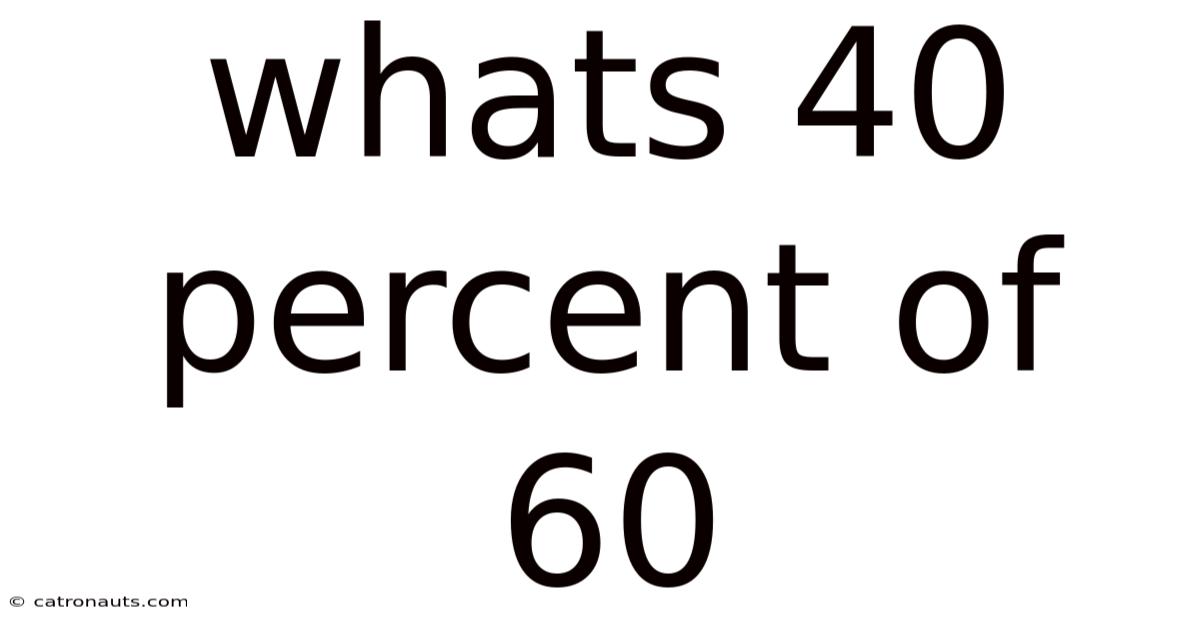
Table of Contents
What's 40 Percent of 60? A Deep Dive into Percentages and Their Applications
Finding 40 percent of 60 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying principles of percentages and their practical applications is crucial for navigating various aspects of life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will not only answer the question "What's 40 percent of 60?" but also provide a comprehensive exploration of percentages, their calculation methods, and real-world examples.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). It's a way of expressing a proportion or a part of a whole. For example, 50% means 50 out of 100, or one-half. Similarly, 10% means 10 out of 100, or one-tenth. Percentages are used extensively in various fields because they provide a standardized and easily understandable way to compare quantities and proportions.
Methods for Calculating Percentages
There are several ways to calculate percentages, and understanding these methods is key to mastering percentage problems. Let's explore the most common approaches:
1. Using the Formula:
The most straightforward method is using the basic percentage formula:
- Percentage = (Part/Whole) x 100
In our case, we want to find 40% of 60. Here, 60 is the whole, and we want to find the part that represents 40%. Applying the formula:
- Percentage = (40/100) x 60 = 0.4 x 60 = 24
Therefore, 40% of 60 is 24.
2. Using Decimal Conversion:
Another efficient method involves converting the percentage to a decimal. To convert a percentage to a decimal, divide the percentage by 100. For example, 40% becomes 0.4 (40 ÷ 100 = 0.4). Then, multiply the decimal by the whole number:
- 0.4 x 60 = 24
This method is particularly useful when dealing with more complex percentage calculations.
3. Using Fractions:
Percentages can also be expressed as fractions. 40% can be written as 40/100, which simplifies to 2/5. To find 40% of 60, multiply the fraction by the whole number:
- (2/5) x 60 = 24
This method provides a visual representation of the proportion and can be helpful for understanding the underlying concept.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in many real-world situations. Here are a few examples:
-
Discounts: Stores frequently offer discounts on merchandise. For example, a 20% discount on a $100 item means you save $20 (20% of $100 = $20).
-
Taxes: Sales taxes, income taxes, and other taxes are often expressed as percentages. Understanding how to calculate taxes is crucial for budgeting and financial planning.
-
Tips and Gratuities: When dining out or receiving services, tipping is customary. Tips are usually calculated as a percentage of the total bill.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding interest calculations is essential for managing personal finances.
-
Financial Statements: Financial statements, such as income statements and balance sheets, use percentages extensively to represent ratios and proportions of various financial elements. For instance, profit margin is expressed as a percentage of revenue.
-
Statistical Analysis: Percentages are fundamental to statistical analysis. They help represent proportions within datasets and are vital for interpreting statistical findings. For example, understanding survey results often requires calculating percentages to represent the distribution of responses.
-
Scientific Data: In scientific studies, percentages often represent the proportion of a certain outcome in an experiment or the concentration of a substance in a solution.
-
Sports Statistics: Batting averages, free-throw percentages, and other sports statistics are expressed as percentages, helping to understand player performance and team dynamics.
Solving More Complex Percentage Problems
While finding 40% of 60 is relatively simple, understanding how to approach more complex percentage problems is equally important. Consider these scenarios:
-
Finding the Whole: If you know the percentage and the part, you can find the whole. For example, if 25% of a number is 15, you can set up the equation: 0.25x = 15. Solving for x, you find the whole number is 60.
-
Finding the Percentage: If you know the part and the whole, you can find the percentage. For example, if 12 is part of a whole of 48, you can calculate the percentage as (12/48) x 100 = 25%.
-
Percentage Increase/Decrease: Calculating percentage increase or decrease involves finding the difference between two numbers and expressing it as a percentage of the original number. For example, if a price increases from $50 to $60, the percentage increase is [(60-50)/50] x 100 = 20%.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate percentages?
- A: The easiest way depends on your comfort level with different mathematical operations. Using the decimal conversion method (converting the percentage to a decimal and multiplying by the whole number) is often the quickest and most efficient approach.
-
Q: How can I improve my understanding of percentages?
- A: Practice is key! Solve various percentage problems using different methods. Start with simple problems and gradually work your way up to more complex ones. Real-world applications will further solidify your understanding.
-
Q: Are there any online tools or calculators for calculating percentages?
- A: Yes, numerous online percentage calculators are readily available. These tools can help you check your work and expedite calculations, especially for more intricate problems. However, understanding the underlying concepts remains crucial.
-
Q: Why are percentages important?
- A: Percentages provide a standardized and easily understandable way to represent proportions and compare quantities. Their application extends across numerous fields, making them an essential tool for understanding and interpreting data in various contexts.
Conclusion
To reiterate, 40% of 60 is 24. However, the significance of this seemingly simple calculation extends far beyond a single arithmetic problem. Understanding percentages is a fundamental skill with wide-ranging applications across numerous disciplines. By mastering the different methods of calculating percentages and understanding their real-world applications, you equip yourself with a powerful tool for navigating various aspects of life, from personal finances to professional endeavors. The ability to confidently and accurately work with percentages will undoubtedly enhance your analytical skills and problem-solving capabilities. Continue practicing and exploring different scenarios to reinforce your understanding and build confidence in tackling percentage-related challenges.
Latest Posts
Latest Posts
-
1 Teaspoon Honey In Grams
Sep 16, 2025
-
28 5 40 As A Percentage
Sep 16, 2025
-
Topics For A Slam Poem
Sep 16, 2025
-
7 To The 3rd Power
Sep 16, 2025
-
17 Out Of 20 Percentage
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Whats 40 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.