X 1 2 X 3
catronauts
Sep 17, 2025 · 5 min read
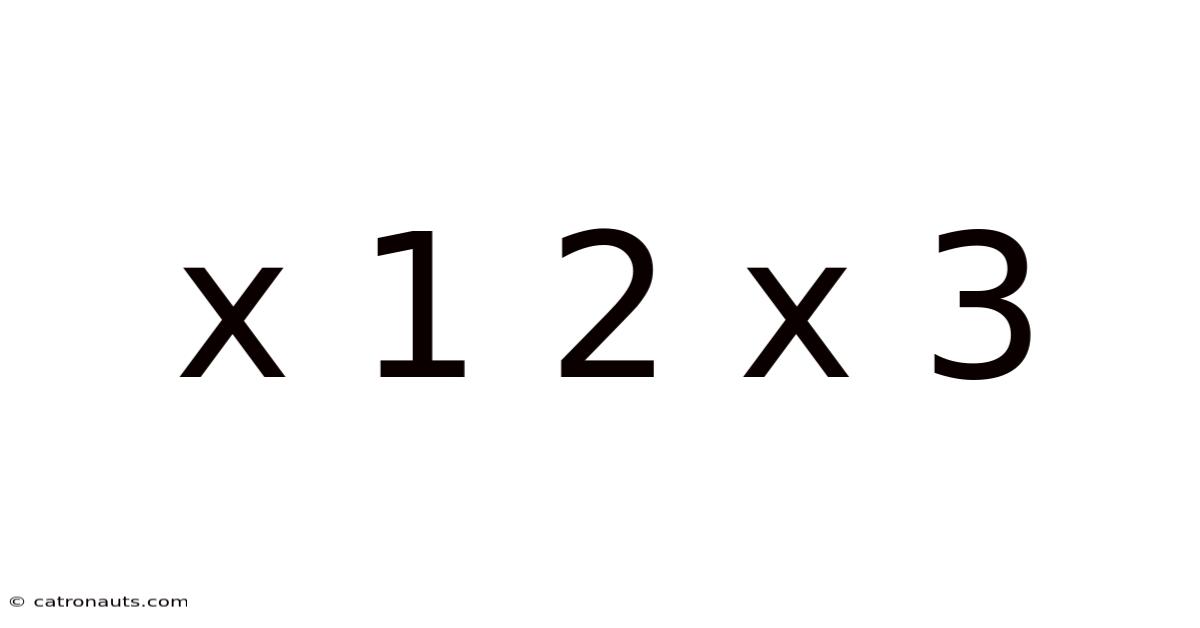
Table of Contents
Decoding the Pattern: Exploring the Mathematical Sequence x 1 2 x 3
This article delves into the fascinating mathematical sequence represented by "x 1 2 x 3." We'll explore various interpretations of this pattern, examining potential mathematical operations, underlying rules, and possible extensions. Understanding this seemingly simple sequence unlocks deeper insights into number patterns and problem-solving strategies. Whether you're a math enthusiast or simply curious, let's unravel the mystery behind x 1 2 x 3 together.
Understanding the Ambiguity: Multiple Interpretations
The beauty of "x 1 2 x 3" lies in its inherent ambiguity. The 'x' acts as a wildcard, allowing for multiple interpretations depending on the assumed mathematical operations. This ambiguity makes the sequence a great tool for practicing analytical thinking and exploring different problem-solving approaches. Let's look at several possibilities:
1. Arithmetic Sequence with an Unknown Common Difference
One interpretation is that this represents an arithmetic sequence where 'x' represents the first term and the common difference is unknown. In this case, we have the sequence: x, x + d, x + 2d, x + 3d, x + 4d where d is the common difference. We're given that:
- Second term: x + d = 1
- Third term: x + 2d = 2
- Fifth term: x + 4d = 3
This provides a system of three equations with two unknowns (x and d), which can be solved using simultaneous equations. Subtracting the first equation from the second yields d = 1. Substituting this value into the first equation gives x = 0. This interpretation suggests the sequence is: 0, 1, 2, 3, 4.
However, this interpretation doesn’t explain why the fourth term is missing.
2. Geometric Sequence with an Unknown Common Ratio
Another possibility is that this is a geometric sequence. If 'x' is the first term and 'r' is the common ratio, we would have: x, xr, xr², xr³, xr⁴. This gives us the equations:
- xr = 1
- xr² = 2
- xr⁴ = 3
Dividing the second equation by the first gives r = 2. Substituting this into the first equation gives x = 1/2. This suggests the sequence is: 1/2, 1, 2, 4, 8... This doesn’t match the provided sequence precisely but illustrates the application of geometric sequence principles. The lack of a clear fourth term makes a perfect geometric progression unlikely.
3. Sequence with Alternating Operations
We could hypothesize that the sequence involves alternating operations. For example, the sequence could be generated by:
- x + 1 = 1 => x = 0
- 1 + 1 = 2
- 2 + x = 3 => x = 1
This leads to a sequence with alternating addition of 1 and an unknown value 'x'. This lacks consistency as 'x' changes between 0 and 1.
4. Interpolation and Missing Terms
Perhaps the sequence is not strictly arithmetic or geometric, but uses interpolation or implies missing terms. We could consider:
- A sequence where 'x' values are inserted between consecutive integers, implying a hidden underlying pattern.
- A modified arithmetic sequence where there are gaps in the sequence which could be filled in by some mathematical rule.
Further investigation of potential underlying rules would be needed to verify such hypotheses.
Exploring Potential Mathematical Functions
Let's move beyond simple sequences and explore the possibility that the pattern is defined by a more complex mathematical function. This could involve:
-
Polynomial Functions: Could the sequence be modeled by a polynomial function where 'x' is a variable? We could attempt to fit a polynomial of degree 4 (or higher) to the given data points. However, this would require more data points to constrain the polynomial's coefficients adequately.
-
Piecewise Functions: A piecewise function could define different rules for different parts of the sequence. This could account for the apparent discontinuity in the given values.
-
Recursive Functions: A recursive function could define each term based on the preceding term(s). The lack of clarity about the fourth term makes it hard to identify this pattern.
The complexity of these approaches highlights that without further information or context about the underlying rules governing the sequence, it's impossible to define a definitive mathematical function.
The Importance of Context: Solving Mathematical Puzzles
The ambiguity of "x 1 2 x 3" underscores the critical role of context in solving mathematical puzzles. Without additional information, multiple interpretations are possible. Here's where considering context comes into play:
-
Origin of the Sequence: Where did this sequence originate? Knowing the source (a textbook problem, a coding challenge, a real-world application) could provide crucial clues.
-
Surrounding Information: Are there any accompanying instructions, diagrams, or examples that could shed light on the intended interpretation?
-
Underlying Assumptions: What assumptions are implicitly made about the nature of the sequence (e.g., is it linear, continuous, discrete)?
Solving mathematical problems often involves a process of deduction and inference, where we make educated guesses based on available information and refine our hypotheses based on testing and feedback.
Expanding the Scope: Similar Mathematical Puzzles
This puzzle shares similarities with many other mathematical brain-teasers that require creative problem-solving and the ability to think outside the box. Examples include:
-
Number Series Completion: Completing number series or patterns involves identifying the underlying rule and extending the series accordingly.
-
Cryptarithmetic Puzzles: Cryptarithmetic puzzles involve replacing letters with digits to solve an arithmetic equation.
-
Logic Puzzles: Many logic puzzles rely on identifying patterns and relationships between elements to arrive at a solution.
These puzzles help develop essential problem-solving skills, including analytical thinking, pattern recognition, and the ability to formulate and test hypotheses.
Conclusion: The Power of Ambiguity in Mathematics
While a definitive answer to "x 1 2 x 3" remains elusive without further context, exploring its multiple interpretations reveals the power of ambiguity in mathematics. It encourages us to think critically, explore different approaches, and appreciate the richness and diversity of mathematical patterns. The apparent simplicity of the sequence hides a wealth of possibilities, underscoring the beauty and challenge of mathematical problem-solving. The exercise serves as a valuable reminder of the importance of careful consideration, attention to detail, and creative thinking when approaching mathematical challenges. Further information would be required to obtain a precise and specific solution. However, the multiple approaches illustrated here demonstrate the power of exploring various mathematical concepts to tackle seemingly simple problems. This puzzle, therefore, isn’t just about finding a solution; it’s about the journey of discovery and the development of critical thinking skills.
Latest Posts
Latest Posts
-
Torque Of A Motor Calculation
Sep 17, 2025
-
16 45 As A Percent
Sep 17, 2025
-
Fun Facts About Little Penguins
Sep 17, 2025
-
Schools In The Victorian Times
Sep 17, 2025
-
Human Resource Management Test Questions
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about X 1 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.